舟山长江江海联运铁矿石运价指数的研究

刘海嵩+金卓+李慧

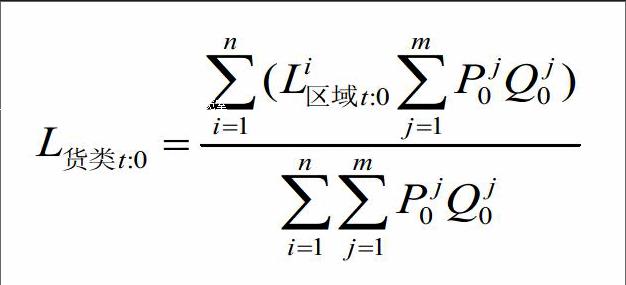
摘 要：2016年宁波-舟山港成为全球首个货物吞吐量突破9亿吨大港，为了加快推进江海联运，国务院正式批复同意设立舟山江海联运服务中心，定位大宗散货的中转服务和高端航运服务。舟山至长江江海联运市场起步较晚，发展迅猛，行政主管部门、投资经营人急需相关运价指数，以反映供需基本关系，评估投资建设效果，提供交易参考。本文以舟山长江联运最大的铁矿石为例，构成了舟山长江联运铁矿石运价指数体系，创新了指数计算模式，采集历史数据，采用相关系数检验新模式，提出后续检验模式方法，进一步丰富了运价指数相关理论，为创建其他指数提供范例与借鉴。

关键词：江海联运；铁矿石；运价指数

中图分类号：U695.2 文献标识码：A 文章编号：1006—7973（2018）2-0016-06

2011年6月国务院批复设立“浙江舟山群岛新区”以来，地处长三角龙眼的舟山群岛发展成为全国大宗货物的聚集度较高、交易规模较大、品种齐全的有一定影响的大宗货物交易、航运贸易市场，辐射长三角洲及国内南北沿海城市地区。2016年国内沿海港口至长江的货物运输量9.9亿吨，舟山到长江的货物运输量1.39亿吨，长江出海货运量3.3亿吨，长江至舟山的货物运输量817万吨。舟山市域港口货物吞吐量4.26亿吨，其中外贸吞吐量1.31亿吨，进江主要货物为铁矿石、矿建材料、石油及其制品、煤炭、粮食等，满足长江沿线大型钢厂、电厂、炼油化工厂、基建项目等需求。

随着水水中转、江海联运等多式联运推进，宁波舟山至长江联运市场，尤其是铁矿石运输将继续快速发展。《宁波-舟山港总体规划（2014-2030年）》，到 2020年总设计通过能力达到1.8亿吨，新增堆存能力700万吨，总堆存能力达到1500万吨。《特定航线江海通航船舶建造规范》和《特定航线江海通航船舶检验暂行规则》颁布后，宁波舟山港至马鞍山2万级江海直达首艘散货船在舟山正式接水。2017年11月长江航运“645工程”加快推进，2020年安庆至武汉航道最低维护水深将达6米，武汉到宜昌最低维护水深将达4.5米，1.3 万吨级内河船和1万吨级海船将直达武汉。远期，三峡新通道8米的最低门槛水深，保证万吨级大型船舶通过三峡坝区，将进一步增加江海直达运量与运距。

为了提升舟山群岛港口商贸在国际航运业的影响，打造成全国乃至亚太地区最具规模的现代港口贸易服务基地，浙江省《舟山江海联运服务中心建设实施方案》明确加快形成“舟山价格”、“舟山指数”，深化海上丝路指数开发，探索形成江海联运“运价指数”等衍生产品，增加价格指数在亚太地区乃至全球中的影响力。宁波发布了宁波海上丝路指数，包括出口集装箱运价指数、航运经济指数、海上丝路贸易指数。上海航运交易所发布了13个海上运输综合指数。研发舟山铁矿石运价指数ZSFI（CHINA ZHOUSHAN RIVER-SEAFREIGHT INDEX），填补了江海联运指数空白，完善了中国航运运价指数体系。航运运价指数的市场影响和社会效果取决于航运指数科学性与权威性，舟山长江江海联运直达运输作为新兴运输方式，其市场结构、运输组织方式和航线运营具有一定的独特性，必须解决与发布指数有关的一系列技术与应用问题。

1 铁矿石运价指数构建

1.1 样本航线与样本单位的确定

航运指数中的样本航线就是统计学指数理论上的规格品，规格品是为了反映全部商品的价格变化情况而科学地选择部分具有代表性的商品，样本航线是编制指数时被选择的代表性航线。样本航线确定原则：一是代表性，选择某货类运输市场最具有代表性的航线，流向、运输量基本稳定。样本航线的运量必须在该地区市场中占有相当的比例。二是多样性，各货类指数具有多种代表性航线，覆盖主要船型、运输线路，囊括不同的区域。

目前，舟山长江铁矿石联运涉及的长江港口主要包括太仓、南通、张家港、江阴、靖江、常州、泰州、扬中、镇江、南京、马鞍山、芜湖、武汉、湘潭等，主要存在三种运输组织方式，即远洋船减载运输江苏南京以下河港，国内海船直接进江运输，江海直达船舶运输。南京以下主要船型为10-20万吨级减载海船、1.5-6万吨二程海船，南京以上海船以0.5-1.3万吨直达船、0.3-0.8万吨内河船为主。舟山至泰州、扬中、湘潭的运量偏小，难以收集连续的运价信息，不入选样本航线，铁矿石运价指数的规格品为剩下的11条航线。基本分类上据航道水深、主要船型、航距等因素，以江阴、南京为节点可划分三段，但考慮2020年江苏段航道水深将均可达到12.5米，船型也将以3-6万DWT为主，三区段将自然演变为两区段，在指数运行时选择二区段方案进行划分。

发展前景较好的中小航运企业。全面性原则，兼顾不同的经济类型，国有企业外、外企、合资公司等各类型企业。所有样本单位航线覆盖所需航线，每条航线的样本企业3-5家。企业航线具有代表性，样本企业在样本航线的运输业务占本企业业务总量的10%以上，货源基本稳定，样本企业市场总份额超过该航线运输总量的5%。公司航线具有流动性，主要船型在报告期内有一定数量的货物运输交易行为，较大规模的投资或运输需求不至于引起价格指数值的剧烈变化。据此选取宁波舟山地区典型企业，如宁波金辉物流公司、宁波北仑船务公司、舟山兴港海运公司、舟山协海航运公司、新一海海运公司，上海地区上海海一航运公司，江苏地区南京鑫武海运公司等，安徽地区安徽中联海运公司、安徽华远海运公司，湖北地区华航集团物流公司、武汉创新江海公司、武汉江裕海运公司，湖南地区岳阳欣港物流公司等。

1.2 计算方法的选择

舟山江海联运指数适用加权综合指数法中的拉氏指数原理编制，主要考虑：一是舟山至长江联运总运量规模达1.39亿，11条铁矿石联运航线具有联运市场的代表性，满足流动性要求，同时航线的同度量因素-运量已经梳理，具备应用加权综合指数法的基本条件。二是将同度量因素相对固定在报告期，更能精确反映价格的变化趋势。如果固定在报告期，联运不充分的南京以上的联运比例将逐渐加大，其权重也将越来越大，导致运价波动逐渐变小。三是拉氏公式，没有考虑运量变化给运价本身的影响，在正常情况下运量的变化对运价短期影响微乎其微，剧烈变化时才有明显短期影响。运量长期积累变化，影响实际运价的权重，可以通过定期修正权重的方法进行处理，使得指数编制工作高效而精确。endprint

在实际的价格指数编制过程中，必须对基本的拉氏公式（1-1）进行变形或推导。

公式（1-1）为基本拉式公式，适用范围：简单航线指数计算，航线基本固定的货类指数计算。公式（1-2）为变形公式之一，可称为“航线权数分配法”，其含义明确，将基期1000点按照分配每个航线单位运价指数，报告期价格点乘单位运价指数，累加后得出报告期指数。适用范围：航线固定的货类指数计算。公式（1-4）为变形公式之二，可称为“拉式链式公式法”，每次计算调查结果时，只需要计算每一典型航线本期与上期的价格对比情况，而不用取得每一典型航线的具体价格，就可得出全部的指数结果。适用范围：经常出现航线缺失、市场份额变化引起的典型航线替换等情况，使价格指数编制工作具有可操作性与灵活性。

1.3 权重的确定

成分指数生成综合指数时以各成分指数∑PQ（各样本航线的基期运输金额）为权重。各货类指数或区段指数的权重反映了对应分货类市场或区段市场在综合市场中的重要程度，权重计算方法直接影响到综合指数的全面性与灵敏度。

舟山长江铁矿石联运市场划分南京以上、南京以下两个区段，现有两个区段市场运输结构明显不平衡，南京以下运输量占据86%，权重明显偏大，控制了指数总体走势，忽视南京以上市场多数个体的真实变化。同时，未来几年市场的铁矿石运量结构非常确定会发生明显变化，南京以上增速明显高于饱和的南京以下市场，需要重新确定权重。确定权重常用的方法： 主观赋权法，如AHP（层次分析法）、Delphi（专家法）等。客观赋权法，客观赋权法在确定权重系数的过程中避免了人为因素的干扰，能够较为客观的反应各评价指标在综合评价指标体系中的重要性，如变异系数法、CRITIC赋值法、熵值法。

熵值法和变异系数法的计算结果较为接近，“南京以下”较“南京以上”冲突性小、变异性小、信息量小，前者客观权重小于后者，修正了“南京以下”运量较大，区域指数占比偏大的问题。CRTIC法对运量调整出现相反的结果，主要原因在于特征指标只有两种，特征相关系数矩阵为两阶对称矩阵，矩阵列之和相等，特征间的冲突性无法体现，特征指标的信息量仅取决于特征类间的对比强度（标准差），此种情况CRTIC法明显劣于变异系数法，因此取熵值法和变异系数法的平均修正值。“南京以下指数”、“南京以上指数”，两者运输量（权重）比例按照62.7%：32.8%分配与控制。

1.4 基期的确定

基期是价格比较的基础时期，是科学编制价格指数的基础。确定基期有两个含义：一是确定了以该基期期间的平均价格为基数，即该基期整个期间的定基指数定为1000；二是利用或参照该基期期间的总销售额的比重而确定了未来计算指数时的权数。一般选在供需相对平衡、价格相对合理时期。2015年航运价格处于低迷期，2016第四季度逐步止跌回升，2017年2月至3月波罗的海指数从690点上涨至1200点，国内海运、内河运输价格出现明显上升，2017年1月国内外航运业量价齐升的起点，企业盈利面大幅回升，运力与运量相对平衡，试运行期间选择2017年1月为舟山长江江海联运铁矿石运价指数的基期。

2 测试步骤与结果

2.1 計算步骤

（1）典型航线价格指数计算。计算某样本企业中某典型航线平均价格，采用简单算术平均法计算不同航次航线的平均价格。样本单位同时提供长协价、市场价时，按照各计50%算术平均；仅提供一种价格时，长协价的样本单位数量不多于市场价的样本单位数量。航线的定基指数按照公式（1-4）计算。

（2）区域价格指数计算。样本企业中报送典型航线运价连续时，某样本企业中某典型航线平均价格、航线的定基指数采用公式（1-4）计算，各区域的样本单位基期运量之比与市场运量结构或修正运量接近。样本企业中报送典型航线运价不连续时，计算某样本企业中某典型航线平均价格环比相对数，计算区域某典型航线运价的环比指数，即经营该典型航线的所有样本企业中所有该条航线平均价格环比相对数的几何平均值。区域综合指数按照公式（1-1）或公式（1-4）计算。

2.2 计算结果

3 结论

经拉氏基本公式验算舟山ZSFI指数的准确性，其综合指数、航线指数结果与变形公式1-4的计算结果完全一致，证实公式推导正确。变形公式能保证综合指数权重不变，航线权数及时修正，灵活处理航线变更情形。对不平衡区域指数，采用客观赋权法完全可行，符合市场发展趋势与指数工作规律，同时客观赋权法更适合编程，在大数据时代可实现指数工作的自动化与智能化。

经检验，ZSFI与CBFI、BDI、CJFI的相关系数分别为0.419964，0.3642667，-0.070881，T值也较低，相关性较弱。南京以下的航线与CBFI、BDI呈现正相关，舟山-张家港、舟山-常州航线指数与CBFI、BDI相关系数较高。舟山至南京以上航线指数与CBFI、BDI、CJFI的相关指数均较低。南京以下市场相对成熟，接近长江口的航段能航行更多船型的海船，市场化化程度越高，容易受沿海市场的影响。南京以上航段存在独特环境因素，货主单位对运价控制能力较强，市场上多为长协价，难以正常反映供需关系，航线指数计算结果与实际情况相吻合。

目前，没有形成足够多的指数结果数据，暂时无法格兰杰因果检验。运行一段时间后，将通过ZSFI与其他指数逻辑上关系来检验综合指数模型的适应性，先行对数据平稳检验，后协整检验，分析变量之间是否具有长期稳定的均衡关系，最后格兰杰因果检验。如果变量之间存在协整关系，则至少存在一个方向上的Granger 原因。在做Y对其他变量（包括自身的过去值）回归时，如果把X滞后值包括进来显著地改进Y的预测，X就是Y的格兰杰原因。通过各项检验，不断修正技术方案，树立指数权威性，为推广指数在行政决策、船货交易、衍生品交易应用中创造良好的先决条件。endprint