应用状态方程预测液化天然气的热物理性质

苑伟民

中石化北海液化天然气有限责任公司，广西北海 536000

液化天然气通常储存在压力为5～25 kPa、温度为-163℃左右的低温储罐内。液化天然气管路系统主要用于天然气液化装置与液化天然气装卸码头装置，液化天然气装卸码头装置与接收终端的液化天然气储罐，以及液化天然气储罐与气化器的连接[1]，管路内的平均压力在1 MPa左右，平均温度在-156℃左右[2]。本文选取SRK、PR、LKP和MBWRS[3]四个状态方程，对罐内储存和管路输送状况下的液化天然气的热物理性质进行预测，并对预测的结果进行分析、讨论。

目前，用于液态烃类计算的状态方程主要有SRK、PR、LKP和MBWRS四个状态方程，其中用于计算液化天然气物性的主要是LKP状态方程[2，4，5]，SRK和PR方程[6]多用于计算烃类的汽液平衡[7-15]，由于MBWRS状态方程[16]形式复杂，文献中较少用于液态计算[1]。本文运用四个状态方程对液化天然气的热力学性质进行预测，重点对MBWRS状态方程在预测液化天然气热物理学性质方面的适用性进行分析。

1 状态方程

1.1 Soave-Redlich-Kwong（SRK）状态方程[16]

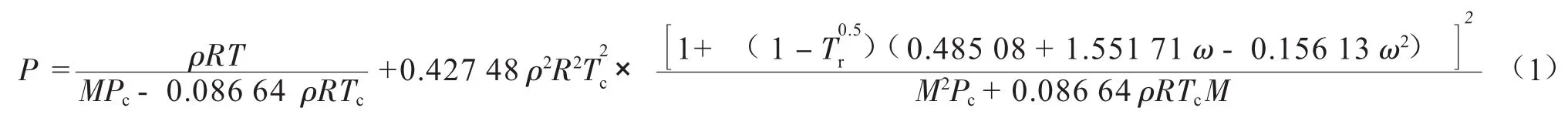
式中：P为系统压力，kPa；ρ为流体密度，kg/m3；R为通用气体常数，kJ/（kmol·K），取8.314 3；T为系统温度，K；M为流体平均摩尔质量，kg/kmol；ω为Pitzer偏心因子；Pc为临界压力，kPa；Tc为临界温度，K；Tr为对比温度，无量纲。

1.2 Peng-Robinson（PR）状态方程[16]

两参数立方方程，如SRK和PR状态方程，其最佳适用范围为：对于大多数烃类，偏心因子ω为0.35左右，亦即临界压缩因子Zc为0.26左右；对于氟化氢，ω为0.12左右，对于水，ω为0.229左右，对于惰性气体，ω为0.286～0.311[10-11]。

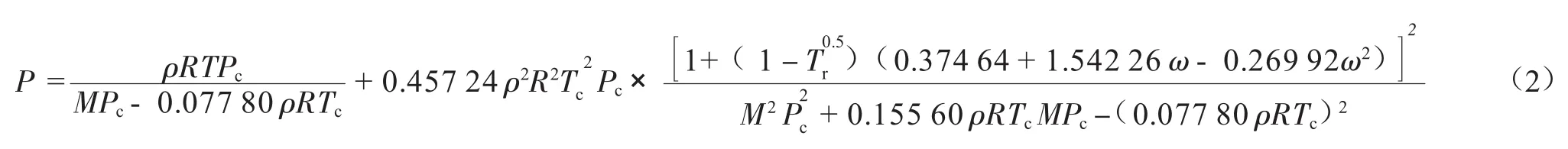
1.3 Lee-Kesler-Plocker（LKP）状态方程[4]

混合物的虚拟临界属性表达式为：

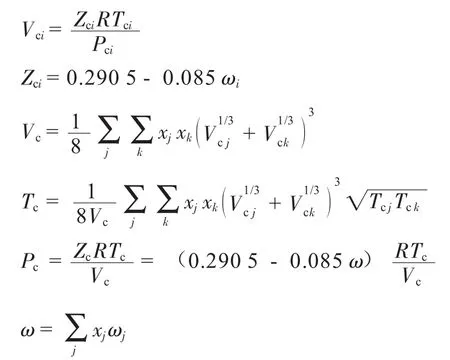
式中：Pr、Tr、Vr分别表示对比压力、对比温度、对比摩尔体积，无量纲；上标（0）、（r） 分别表示简单流体和参考流体；下标i、j、k代表流体的组成；下标c表示临界状态；Vci表示第i种流体的临界体积，kmol/m3；Zci表示第i种流体的临界压缩因子，量纲为1；xj、xk分别代表组分j、k的摩尔分数；Tci表示第i种流体的临界温度，K；Pci表示第i种流体的临界压力，kPa；ωi表示第i种流体的Pitzer偏心因子；b1、b2、b3、b4、c1、c2、c3、c4、d1、d2、β、γ为常数，其取值见表1。

表1 常数的取值

1.4 Modified-Benedict-Webb-Rubin-Starling（MBWRS）状态方程[3]

式中：P为系统压力，kPa；T为系统温度，K；ρ为气相或液相的密度，kmol/m3；R为通用气体常数，kJ/（kmol·K），取 8.314 3；A0，B0，C0，D0，E0，a，b，c，d，α，γ为方程中的11个参数[3]。

2 状态方程分析

PR和SRK状态方程广泛应用于工业，特别是炼化和油气储层模拟。这两个状态方程的优点在于需要较少的输入参数（仅需要临界属性和偏心因子这些普通数据），计算时间短，并且能够较好地预测烃类的相平衡，这些对工艺流程设计很重要。然而，这两个方程也有其短处，例如，不能很好地预测液相密度，大约有5%～10%的误差，尤其是在接近临界点时误差更大，对于小于1.333 2 kPa的蒸汽压预测也不十分准确。虽然有这些缺点，SRK和PR方程仍是在工业中广泛应用的立方方程[17-19]。

BWR类型的状态方程属于扩展的维里方程的一种，可以把BWR类型的方程看成是一个封闭的维里方程，其包含的指数项可以看成是关于摩尔密度的无限级数项。最常用的是1972年STARLING K E和HAN M S提出的BWRS状态方程，最近该方程又被扩展应用至25种气体组分[3]。

STARLING KE和HAN M S使用BWRS状态方程成功预测了38种混合物的超过1 400个数据点，包括LPG和天然气（最多包含10种物质）。在温度为-175～238℃和压力为1.013×102～3.447×104kPa条件下预测得到的密度值，与实验数据平均绝对偏差为1.16%；在温度为-157～360℃和压力为3.447×102～1.723×104kPa条件下预测的焓值，与实验的焓值偏差为5.117kJ/kg；在温度为-157～149℃和压力为1.723×103～1.378×104kPa条件下预测的熵值，与实验的熵值偏差为1.21×10-2kJ/（kg·K）。预测了包括正链烷烃、异丁烷、异戊烷、乙烯、丙烯、环己烷、苯、甲苯、氮、硫化氢、二氧化碳、硝酸氧化物在内的2 000个数据点，与实验密度的平均绝对偏差为1.38%，与实验焓值的偏差为4.047kJ/kg，与实验的饱和蒸汽逸度偏差为1.08%[20]。

LKP状态方程可以看成是使用对比态方法表示的BWR型状态方程。

3 计算实例

选取北海液化天然气接收站的工艺参数，对液化天然气的热物理性质进行求解。

3.1 管输液化天然气

取管道输送部分绝对压力为1 000 kPa，温度为-158℃，求得对比压力Pr为0.217 6，对比温度Tr为0.595 7。使用HYSYS2006中SRK、PR、LKP方程求解，对MBWRS自行编程求解，组分见表1，结果见表2。

表1 L NG典型气质组分（体积分数）

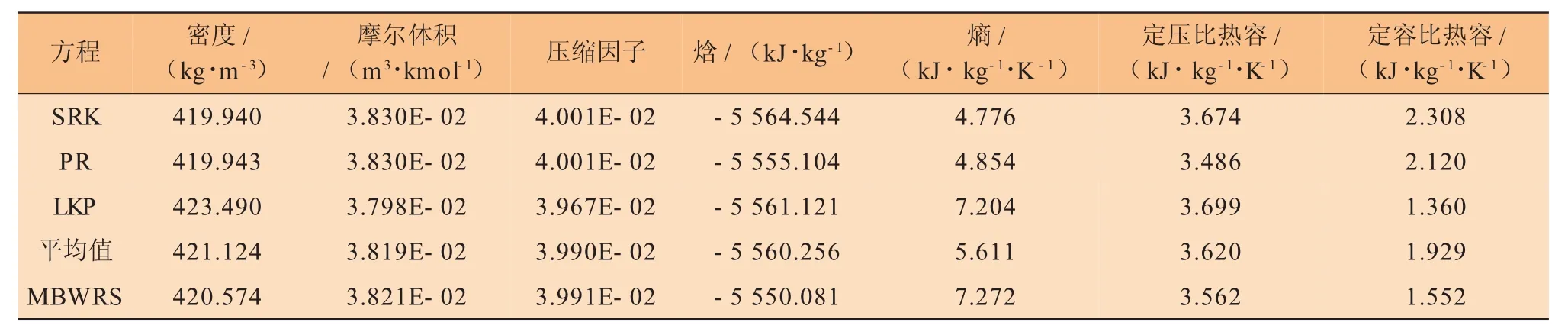
表2 L NG热物理性质预测结果

3.2 LNG储罐内液化天然气

卸船期间，全包容罐储罐最大允许操作压力为25 kPa。取正常操作非卸船工况压力为20 kPa，即绝对压力为121 kPa，温度为-162℃，求得对比压力Pr为0.026 3，对比温度 Tr为 0.575。使用 HYSYS 2006中SRK、PR、LKP方程求解，对MBWRS自行编程求解，结果见表3。

表3 L NG热物理性质预测结果

4 结论

使用SRK、PR、LKP和MBWRS状态方程对液化天然气的热物性参数进行了计算：

（1）从两个实例计算的结果可以看出，第一种工况，SRK、PR和LKP状态方程对密度的预测结果基本一致，MBWRS与SRK、PR状态方程对密度的预测结果相近，LKP方程对密度的预测值与其他三个方程相差较大；第二种工况，MBWRS状态方程对密度的预测值介于四个状态方程之间，MBWRS和LKP状态方程对密度的预测值偏大。

（2）两种工况下，MBWRS方程预测的密度、摩尔体积、压缩因子与SRK、PR、LKP三个方程预测结果的平均值基本一致。

（3）由于预测理想气体焓、熵和比热的经验公式较多，以上方程预测的值相互之间也有较大出入。

（4）虽然两种工况（Tr=0.595 7，Pr=0.217 6与Tr=0.575，Pr=0.026 3） 均超出了MBWRS状态方程的适用范围（Tr≥0.3），但是，从预测结果可以看出，使用MBWRS计算，预测值在一定误差范围内仍然准确。

（5）液化天然气的运输和存储过程的压力和温度条件在MBWRS状态方程的适用范围内，计算结果可靠。

综上所述，将MBWRS状态方程用于液化天然气工艺计算是准确、可行的。

[1]顾安忠，鲁雪生，汪荣顺，等.液化天然气技术[M].北京：机械工业出版社，2004.

[2]陈保东，李庆杰，洪丽娜，等.液化天然气管道输送工艺参数的计算[J].油气储运，2011，30（1）：15-17.

[3]苑伟民.修改的BWRS状态方程[J].石油工程建设，2012，38（6）：9-12.

[4]石玉美，顾安忠，汪荣顺，等.天然气物性的LKP方程求解[J].能源技术，2001，22（2）：62-64.

[5]位雅莉.天然气液化工艺模拟与分析[D].成都：西南石油学院，2004.

[6]苑伟民，贺三，袁宗明，等.求解BWRS方程中密度根的数值方法[J].天然气与石油，2009，27（1）：4-6.

[7]梁平，王治红，李志铭，等.基于SRK状态方程的烃类液相密度计算校正[J].西南石油大学学报（自然科学版），2009，31（3）：118-120.

[8]陈雪，李明.LNG储罐内BOG动态模拟研究[J].油气储运，2008，27（11）：36-40.

[9]熊光德，毛云龙.LNG的储存和运输[J].天然气与石油，2009，27（1）：4-6.

[10]童景山，高光华，高裕品.化工热力学[M].北京：清华大学出版社，1995..

[11]王红，白改玲，李艳辉，等.LNG接收站流程模拟计算[J].天然气工业，2007，27（11）：108-109.

[12]金光，李亚军.LNG接收站蒸发气体处理工艺[J].低温工程，2011，179（1）：51-56.

[13]李朋，邓静.LNG轻烃分离流程的优化研究[J].新疆石油天然气，2010，6（1）：78-81.

[14]李军，吴洪松.液化天然气相平衡计算[J].煤气与热力，2007，27（10）：18-21.

[15]苑伟民，青青，袁宗明，等.输气管道模拟状态方程[J].油气储运，2010，29（3）：194-196.

[16]童景山.流体热物性学——基本理论与计算[M].北京：中国石化出版社，2008.

[17]HASAN O，STANLEY I，SANDER.Modeling vapor-liquid equilibria：Cubic equations of state and their mixing rules[M].United Kingdom：Cambridge University Press，1998.

[18]STANLEYI，SANDER.Models for thermodynamic and phase equilibria calculations[M].New York：MarcelDekker，lnc.，1993.

[19]苑伟民.PR气体状态方程的显式化[J].油气储运，2017，36（5）：532-536.

[20]STARLING K E，HANM S.Thermo data refined for LPG（14）Mixture[J].Hydrocarbon Processing，1972，51（5）：129-132.