软土地区综合管廊基坑工程中的两墙合一地下连续墙长度优化分析

王潇宇

上海市政工程设计研究总院（集团）有限公司 上海 200092

0 引言

随着我国经济发展速度和城市建设步伐的加快，城市对市政管线的需求也在不断加大。近年来，国家陆续颁布相关政策，大力促进综合管廊工程建设。

城市综合管廊工程为一种浅埋型隧道工程，它将电力、通信、供水、燃气等多种市政管线集中敷设并统一管理，其基坑多为宽度窄、开挖较深、纵向极长的狭长型基坑[1]，具有单次开挖面积小、施工周期短等特点，“空间效应”显著。一般认为，狭长型基坑稳定性[2-3]更好，但受基坑宽度影响明显。

基坑工程设计计算一般包括3个方面内容：稳定性验算、支护结构强度设计和基坑变形计算[4]。现有规范推荐计算方法是基于半无限空间、经典土力学理论，未考虑狭长型基坑空间效应对坑内被动区土体强度的影响，造成设计时插入深度过大，引起较大浪费。

1 工程概况

拟建综合管廊工程位于华东某市，为单仓支线型综合管廊，纳入电力、电信、给水管线。综合管廊总长度约1 130 m，标准段高3.9 m、宽3.6 m、壁厚0.35 m、顶板覆土厚度2.95 m。

本工程综合管廊位于现状道路西侧绿地中，管廊外壁距现状道路路边约5.0 m（图1）。道路及人行横道下方设有雨水、污水、配水、信息等多条市政管线。

受周边现有管线、施工工期等影响，拟采用厚450 mm预制地下连续墙“两墙合一”板式支护，即围护墙兼作综合管廊侧墙，设计须同时考虑开挖工况和使用工况。

图1 综合管廊与道路位置关系（单位：m）

按地方规范，本工程基坑开挖深度6.6 m、基坑宽度2.9 m、基坑宽深比仅为0.44，基坑安全等级为一级。计算得：围护墙须坑底以下插入长度10.70 m、围护墙插入比为1.62、插入长度与基坑宽度的比为3.69；坑内设1道H型钢水平内支撑，每幅墙设2根；顶部利用导墙兼作挡土墙，并在预制连续墙顶部预埋钢板，其上焊扶壁工字钢，形成板肋结构（图2）。

图2 综合管廊基坑横剖面示意

围护墙位移、弯矩、剪力包络图及各项安全系数均采用启明星FRWS软件（版本号7.2）计算（图3）。

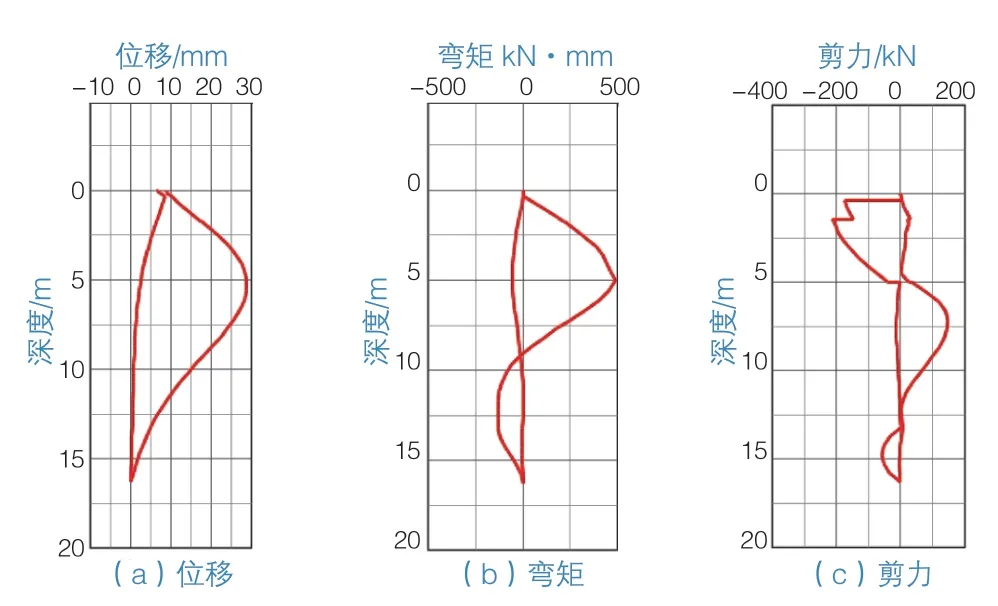
图3 围护墙位移、弯矩、剪力包络图

通过图2可直观地发现，在满足现行基坑规范要求的情况下，围护墙坑底以下插入长度远大于基坑宽度。综合管廊基坑两侧的围护墙将管廊下侧的土体固定在有限的空间内，一侧围护墙位于另一侧被动区土压力滑动面（破坏面）内，起到抗滑移的作用；坑内土体处于有侧限状态，改变被动区土体的应力状态。

现行基坑规范中，土压力计算均是基于郎金土压力理论，将计算剖面模型假定为半无限空间模型，视坑内无限大的区域均开挖至坑底，更适用于常规民用建筑基坑（基坑宽度远大于基坑深度）。

针对本工程，坑底抗隆起（圆弧滑动）安全系数为控制性指标，计算中未考虑对侧土体及围护结构对坑底抗隆起（圆弧滑动）假定滑动面的影响。然而，本工程围护墙坑底以下插入长度远大于基坑宽度，实际开挖暴露的坑底非常有限，空间效应对计算结果有着不容忽视的影响。然而，根据规范计算的结果无法反映狭长型基坑的实际破坏情况，计算结果过于保守。若按此设计、施工，将造成极大的浪费。

2 有限元分析

针对这种情况，通过岩土工程有限元软件建立数值模型，对实际工况模拟、分析，为施工现场开展试验性研究做准备。

2.1 模型参数

本次计算采用硬化模型本构关系，即Harding-soil模型。

Harding-soil模型（简称HS模型）为等向硬化弹塑性模型，模型参数直观明了，具有明确的物理意义，可通过普通三轴剪切和侧限仪固结试验获得，便于工程应用。并且，HS模型在处理回弹（卸载）问题时引入了Eur模量，在模拟、分析开挖问题时具有独特的优势。本次计算中，土体采用硬化模型本构关系，钢支撑采用线弹性本构模型，变形计算考虑流固耦合。

另外，采用摩尔-库伦模型和强度折减法进行稳定性分析。

本工程模型长78 m、深30 m，对于管廊基坑开挖，可认为消除了边界效应的影响。工况按如下考虑：初始模型、插入地下连续墙、降水至坑底、加坑外超载、挖土至第1道支撑底、施加第1道支撑、挖土至坑底（图4）。

2.2 计算结果

通过有限元模型计算，当插入比大于等于0.5时，围护墙水平位移、周边最大沉降量几乎没变化（图5、图6）。

图4 挖土至坑底工况有限元模型

图5 围护墙水平位移与插入比关系

图6 周边最大沉降量与插入比关系

本工程基坑为狭长型基坑，当插入比大于0.5时，插入深度与基坑宽度的比大于1，基坑一侧围护墙已位于基坑另一侧围护墙被动区土体朗金理论的被动区破坏面中，起到抗滑作用。继续增加围护墙的插入深度，已无法提供更大的被动区抗力，对围护墙及周边环境变形影响甚微。

围护墙最大弯矩与插入比的关系与围护墙水平位移、周边最大沉降量与插入比的关系类似（图7），当插入比大于等于0.5时，插入比变化对围护墙最大弯矩影响不大；但是，当插入比等于0.8时，围护墙最大弯矩达到峰值，继续增加插入比，围护墙最大弯矩反而减小[5-7]。

图7 围护墙最大弯矩与插入比关系

利用强度折减法分析插入比对基坑稳定性的影响，基坑安全系数与插入比近似呈线性关系（图8），随着插入比的增大，基坑安全系数增高。

根据该地区工程经验，一般插入比不小于0.8。结合本工程狭长型基坑，将插入比定为0.8，开展现场试验性应用。

图8 强度折减法安全系数与插入比关系

3 结论

本工程管廊基坑为狭长型沟槽，按现有基坑规范计算，本工程基坑围护墙插入比为1.39，插入长度与基坑宽度的比为3.17。若按此计算结果应用、实施，将引起较大浪费。

现行规范中，土压力计算均采用基于半无限空间假定的郎金土压力理论，将计算剖面视坑内无限大的区域均开挖至坑底，更适用于常规民用建筑基坑。

因此，有必要根据本工程实际情况，结合有限元软件建立数值模型，进行模拟、分析，发现：

1）当插入比≥0.5时，围护墙水平位移、周边最大沉降量随插入比增加小幅变化。基坑一侧围护墙已位于基坑另一侧围护墙被动区土体朗金理论的被动区破坏面中，起到抗滑作用。

2）当插入比≥0.5时，插入比的变化对围护墙最大弯矩影响不大；但是，当插入比等于0.8时，围护墙的最大弯矩达到了峰值，继续增加插入比，围护墙最大弯矩反而减小。

3）利用强度折减法分析插入比对基坑稳定性的影响，基坑安全系数与插入比近线性关系，随着插入比的增大，基坑安全系数增高。