基于向量法距离计算的快速圆形区域查询方法
张国宾 王勇 倪凯歌 陈晨


摘要 随着移动网络技术与全球定位技术的发展,GIS信息在军事应用中使用愈来愈频繁,在任务数据保障中,对目标周边区域情报数据的快速查询是一项基本功能。在推进国产化的进程中,部分国产数据库还未集成空间分析功能。本文提供了一种已知两点经纬度,基于向量点乘公式,求出两点对应地心角,计算距离,实现圆形区域查询的方法,同时通过对数据初筛过滤、建立索引等方法进行查询优化,达到快速查询效果。
【关键词】向量点乘距离计算 圆形区域查询初筛过滤 查询优化
随着移动网络技术与全球定位技术的发展,GIS信息在生活、军事应用中使用愈来愈频繁,在任务数据保障中,对目标周边区域情报数据的快速查询是一项基本功能。在推进国产化的进程中,部分国产数据库还未集成空间分析功能。本文提供了一种基于向量法距离计算的快速圆形区域查询方法。
圆形区域查询是常用的一种区域查询方式,通过计算数据库中各POI(商家)或相关方信息与目的目标位置(中心点)的距离,而进行的一种筛选查询。所以圆形区域的查詢重点在于与中心点间的距离计算。
1 计算方法
1.1 常用计算方法
对己知两点经纬度的进行距离计算由多种方法,下边是常用的几种。
(1)己知两点的大地坐标计算距离,设两点大地坐标值为(xl,yl),(x2,y2)则:
式中L是两点之间距离,单位是km。用此公式计算时,要注意两点是否在同一个坐标系内。如果两点不在同一个坐标系内,就须将其中的一点经坐标平移变换到另一点所在的坐标系内。平移公式为:x =x+a、y=y+b,式中a,b是原坐标的原点在新坐标系中的坐标值。
(2)己知两点的空间三维坐标计算距离,设两点空间三维坐标值为(xl,yl,zl),(x2,y2,z2)则:
式(2)中L是两点之间距离,单位是km。用此公式计算时,是将地球近似成球体,地表点都为空间直角坐标系球体表面一点,将经纬度坐标转换为空间直角坐标系坐标,公式(3)如下。
在直角坐标系中,X轴为地心与初始子午线与赤道的交点的连接方向为正向,Y轴为地心向西经90°子午线与赤道交点的方向为正向,Z轴为地心与北极点连接方向为正向,R为地球半径,lat、lon分别为纬度、经度值,x、y、z分别是该点转换后的空间坐标值。
(3)己知两点的经纬度计算两点距离的近似公式,设定A点(latl,lonl)和B点( lat2,lon2)则:
式(4)中L是两点之间距离,单位是度,111.199km是赤道附近10经纬度差对应的距离值。
比较以上三种方法:
第一种方法比较简单,但大地坐标非常用地理信息表示方法,不易获取该值;
第二种方法,采用三维直角坐标系,计算空间两点直线距离,即球面两点间弦的长度,在短距离计算中近似等于地表距离,但在大跨度远距离时,误差较大;
第三种方法,分别计算两点在经纬度方向的弧长值,近似利用勾股定理,获得两点间的弧长。同样,与第二种方法类似,所使用的勾股定理是平面直角坐标系内的计算公式,在近距离内,两点可认为是在同一地平面,但在大跨度远距离时,误差依然较大。
1.2 向量法距离计算
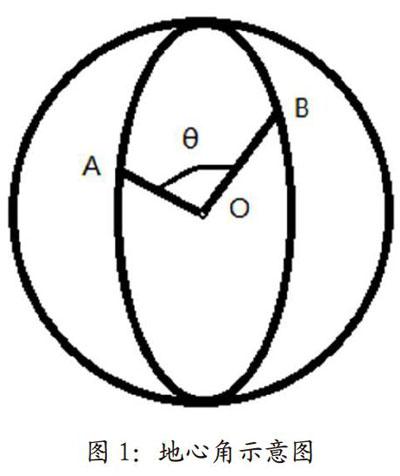
对于球面体,球面弧长,等于球体半径与对应球心角(弧度)的乘积,同理,地球表面两点间距离,可以从两点与地心组成空间角度来计算获得。暂时称该两点与地心组成的角度称为地心角,如图1中所示地表A点( LonA,LatA)与B点(LonB,LatB)与地心O组成的夹角0。
求θ角的方法有多种,可以通过AB弦长度与OA、OB地球半径的长度,根据三角形余弦公式获得,也可以通过三面角余弦公式获的。但其计算过程步骤复杂。本方案采用向量法获取θ角值。OA、OB可认为是两个三维空间向量,θ为向量间夹角,根据向量点乘公式(5)(6)可知,0的余弦等于两向量点乘除以两向量模的乘积。
A、B两点的弧长AB则等于R.θ,θ的单位是弧度。由于地球是椭球型,在WGS-84地球椭球体中,赤道半径为长轴半径R,长6378127km,第一偏心率e2=0.006694379013,
2 设计实现与优化
2.1 设计实现
数据库将采用向量法计算距离方法做成数据库函数,代码实现如下所示:
---Cul JW Distance:通过两点经纬度,计算距离,返回值为两点间距离,单位为km,小数点后4位(分米)
create or replace Function”PUBLIC””CulJW Distance”
(
lonl
double,
latl double,
lon2
double,
lat2 double
)
retum number
1S
pi double:=3.1415926;
EARTH_R number:=6378137; 一地球长轴半径
EART H
E 2double:=0.006694379013;--地球第一偏心率
EARTH B double:=EARTHR*SQRT(l-EARTH_E2);
一地球短轴半径
lathl double;
一纬度1弧度表示
lonhl double;
一经度1弧度表示
lath2 double;
一纬度2弧度表示
lonh2 double;
一经度2弧度表示
DN double;
一两点中间纬度位置地球半径
TranMatrix00 double;
TranMatrix01 double;
TranMatrix02 double;
TranMatrixlo double;
TranMatrixll double;
TranMatrix12 double;
cosangle double;
一夹角余弦值
angle double;
一夹角
begin
lathl:=latl*PIo,/180;
lonhl:=lonl*PI()/180;
lath2:=lat2*PIo,/180;
lonh2:=lon2*PI()/180;
DN:=EARTH_R*SQRT(1-EARTHE2* SIN《lathl+lath2)/2) *SIN《lathl+lath2)/2》;
TranMatrixOO:=COS(lathl)*COS(lonhl);
TranMatrix0 1:=COS(lathl)*SIN(lonhl);
TranMatrix02:= SIN(larhl);
TranMatrixlO:=COS(lath2)*COS(Ionh2);
TranMatrixll:=CO S(larh2)*SIN(lonh2);
TranMarrix12:=SIN(lath2);
Cosangle:=TranMatrixOO*TranMatrixlO+TranMatrixOl*TranMatrixll+TranMatrix02*TranMatrix12;
angle:=ACOS(cosangle);
retum ROUND(DN*angle/1000,4);
end;
在己知某点经纬度(lon,lat),查询L公里内目标数据信息的查询方法可以写为:selectid,culj w_distanee (longitude,latitude,lon,lat)distance from table where distance <=L;
2.2 性能优化
上述查询只是功能实现,但实际在使用中,数据量达到100W时,查询过程中将对整表数据遍历计算比较,耗时达到数秒(105W时,11.63秒),这对于使用过程中时无法容忍的,如何提高效率,可以从减少查询范围、增加查询索引等方面着手。
缩小查询区域范围,对待查询数据进行初筛过滤,将待查询范围缩减为该圆形区域的外切正方形,根据圆形区域半径可计算出该半径对应的圆心角度值,分别在经度方向与纬度方向找到边界最大值,如图2所示,A( Lon,Lat)点周围L公里范围查询时,首先求得在同纬度方向上,L公里对应的经度角么AO'B(0),同经度线上对应的纬度角∠BOC(φ),计算过程中0' B=O' A=OB.Cos( Lat).OB可根据上文中公式(9)进行计算。至此,则可在查询时增加查询限制条件,在一定范围内的进行初步筛选。查询语句变为:select id,culjw_distance(longirude,latitude,Ion,lat) distance from table where distance <=Land longitude between lon-θandlon+θ and latitudebetween lat-φandlat+φ;当然,当0兰1800或Lat-θ<-90°或Lat+θ>90°时,应做相应修订,此处不具体讨论。如此做来,100W级数据查询时间将至百毫秒级(105W是0.28s)。
建立索引是另一种提高检索速度的方法,可以将数据库表中经纬度建立空间索引,但实际测试效果,速度并未明显提升,经查证发现,当查询语句where后的条件中有函数计算时,索引将不被使用,即查询仍然使用的是全表数据的遍历模式。为了能够使索引起到作用,查询语句需要如下更改,先根据初筛条件,将初筛结果集放置一个临时集合中,再对该临时集合内数据进行距离计算。查询语句变换为:select id,culjw_distance(longitude,latitude,lon,lat) distance from (select id,longitude,latitude fromtable where Iongitude between lon-θ and lon+θand latitude between lat-φand lat+φ)tempwhere distance <=L;
在SQL语句执行过程中为了减少数据库对SQL语句硬解析次数,提高使用高速缓存空间软解析的命中率,使用绑定变量法,在此语句中,每次查询变化的只是中心点的经纬度和圆形区域半径,将该三位参数使用绑定变量替换,则查询语句变为:select id,culjw_disrance(longitude,latitude,:lon,:lat) distance from(select id,longitude,latitude from table wherelongitude between lon-θ and lon+θ and latitudebetween lat-φand lat+φ) tempwhere distance<=:L;如此調优之后,百万级数据查询将至毫秒级(105W时4.8ms)
3 结束语
在任务保障中,经常需要快速查询目标周边信息情报数据,在己知目标经纬度和区域范围的情况下,使用本文的方法进行计算简单方便,通过初筛过滤、使用索引等方法优化查询过程,达到快速查询目的,为任务执行提供情报支援保障。
参考文献
[1]胡伟凡,杨恢先,于洪等,基于高斯投影的经纬度距离参数修正方法[J].计算机工程,2010,36 (02):244-246.
[2]韩忠民,知经纬度计算两点精确距离[J].科技传播,2011(06):196-194.
[3]王琼丽,数据库应用系统性能优化研究与实践[D].北京邮电大学,2009: 34-39.
[4]汪照东.Oracle llg数据库管理与优化宝典[M].电子工业出版社,2008: 720-724.

