大跨度铁路钢桁梁柔性拱桥的弹性稳定性

王 青

(江苏燕宁工程咨询有限公司，江苏 南京 210017)

近年来，中国建设了一些外形优美、结构合理的大跨度钢桁梁柔性拱桥，其中，有京沪高速铁路线上的济南黄河大桥[1]、连盐铁路上的灌河特大桥[2]及沪通长江大桥天生港专用航道公铁两用桥[3]等。钢桁梁柔性拱桥是充分发挥连续钢桁梁承载能力和钢箱拱跨越能力的一种新型桥梁构造形式。拱肋和钢桁梁部分杆件的受力形式以受压为主，随着钢桁梁柔性拱桥跨度的增加，钢桁架以及拱肋杆件的长细比也增加。因此，钢桁梁拱桥的稳定问题非常突出[4]，国内、外因桥梁失稳而造成的灾难也时有发生[5]。

桥梁在建设过程中难免会存在一定的初始误差，造成结构发生极值点失稳破坏[6]。但是，结构的线弹性稳定求解比极值点的求解更方便、简单，分支点失稳的临界荷载通常也是极值点极限承载力的上限，并可以通过稳定系数判断结构的最不利受力工况。因此，分析桥梁结构的线弹性稳定可为其施工阶段提供工程参考价值，也是研究桥梁极值点失稳的必要步骤。一些学者针对结构的稳定性做了许多研究[7]。通过分析桥梁运营阶段荷载加载方式和加载顺序对大跨度钢桁梁拱桥稳定性的影响，以及通过研究运营阶段钢桁梁拱桥的失稳形式，发现该类桥梁失稳模态多为局部屈曲。桥梁弹性稳定性研究集中在成桥运营阶段，然而，结构的稳定不仅在桥梁的运营阶段，而且在桥梁的施工阶段也有个别杆件或者结构的局部失稳。因此，作者拟通过建立大跨度钢桁梁柔性拱桥的ANSYS和MIDAS有限元模型，分析桥梁在施工阶段和运营阶段不同荷载形式下的稳定性，并获得相应的失稳模态。

1 静力弹性稳定研究方法

第一类稳定是完善轴心受压杆件发生的失稳形式，发生第一类失稳时，结构的荷载与挠度的关系曲线呈现出2种可能的平衡途径。由于同一个荷载点出现了平衡分叉现象，因此其失稳也称为平衡分叉失稳。通过假定结构应力与所受荷载呈线性关系，求解结构第一类稳定则衍生为求解方程特征值问题，而得到结构弹性失稳的临界荷载[5，8-12]。

在稳定平衡状态，考虑轴力对弯曲变形的影响，根据势能驻值定理，建立结构的平衡方程：

([KE]+[KG]){U}={P}。

(1)

式中：[KE]为结构的弹性刚度矩阵；[KG]为结构的几何刚度矩阵；{U}为节点位移向量；{P}为节点荷载向量。

(2)

式中：λi为第i阶特征值；{φi}为与λi对应的特征值向量，是相应该阶屈曲荷载时屈曲模态。

由特征值屈曲分析，得到λi和{φi}，即屈曲荷载系数和屈曲模态，相应的屈曲荷载为λi{P0}。

2 有限元模型与工程应用

2.1 工程背景

某钢桁梁柔性拱桥为全长996 m的双线中-活载铁路桥，主桥跨径为(138+360+360+138) m，主梁形式为两片主桁架组成宽15 m的钢桁梁，主跨的宽跨比1/24；双主跨的拱肋矢高为65.0 m，矢跨比1/4.67，在钢桁的3个中支点处布置高为16 m的下加劲，主桥结构形式如图1所示。桥面是由横梁和贯穿横梁的纵梁组成的明桥面形式，纵梁在横桥向间距2 m，纵梁间通过系杆相连。

图1 全桥立面布置(单位：mm)Fig.1 Elevation layout of the full bridge(unit：mm)

2.2 有限元模型及计算方法

为了准确分析结构中拱肋、钢桁梁及吊杆的受力状态，钢桁梁柔性拱桥采用ANSYS和MIDAS软件同时建立模型，并进行计算和相互校核。在ANSYS中，利用BEAM188单元和LINK8单元分别模拟拱肋、钢桁梁以及吊杆。而在MIDAS中，则利用梁单元和桁架单元形式，建立全桥模型。在这2种模型中，除纵梁外的所有杆件的节点均采用共用节点连接。在纵梁断开处的处理中，ANSYS中采用约束方程的形式，而MIDAS中则是采用弹性连接进行释放约束，保证有限元模型中纵梁间只传递剪力，不传递弯矩和轴力。计算时，将每个吊杆间的拱肋细分成5个梁单元，上、下弦杆在每个节间分成5个梁单元，竖杆和斜杆分为4个单元，确保有限元模型准确地模拟结构的受力行为。ANSYS有限元模型如图2所示。

图2 全桥有限元模型Fig.2 Element model of the full bridge

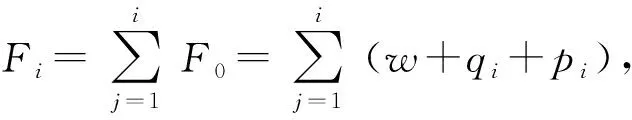
λ={F}cr/(w+∑qi)。

(1)

式中：{F}cr为极限承载力；w为结构的恒载；pi为结构上作用的活荷载；λ为结构稳定系数。

3 计算结果

3.1 施工阶段线弹性稳定承载能力分析

为了合理地分析钢桁梁拱桥在荷载作用下的力学行为，必须对其受到的荷载进行准确的模拟。钢桁梁柔性拱桥在施工过程中结构承受的荷载有结构自重(主体结构和临时结构)、架梁吊机荷载(满载和空载)、张拉力(墩旁托架、边跨后锚和拱肋水平拉索)及其他的施工荷载。采用2种风荷载：正常施工风荷载(基本风压W0=0.28 kN/m2)和抗台验算风荷载(基本风速V0=35.4 m/s)。

根据大跨度钢桁梁柔性拱连续梁桥的结构特点，确定该桥梁上部结构的施工方案。钢桁梁采用悬臂拼装，其边跨有拼装支架，采用在临时支架上向中跨拼装；中跨采用双悬臂拼装。为了保证主跨的稳定性，在2个主跨跨中设置合龙口和4个临时墩。钢桁梁合龙后，在其上利用架梁吊机，由跨中向两侧倒退安装拱肋卧拼支架和钢拱；每跨拱肋分为3段拼装，两侧拱肋在支架上原位拼装，中间段拱肋通过架设在临时墩上的提升塔架提升至设计位置，提升到位后进行拱肋合龙(每跨拱肋设置有2个2 m合龙段)，最后安装吊杆，其施工分8个阶段：① 基础、墩身、临时墩及墩旁托架施工；② 在边跨临时支架上拼装钢桁梁和在中主墩的托架上拼装墩顶钢桁梁；③ 自边主跨向跨中单悬臂拼装桁梁和自中主墩向跨中双悬臂对称拼装桁梁，直至合龙段；④ 张拉中主墩临时扣索，通过临时扣索调整合龙标高，合龙钢桁梁中跨；⑤ 在钢桁梁上弦安装拱肋的支架，拼装拱肋；⑥ 撤出桥面吊机，提升架提升拱肋并拆除拱肋支架；⑦ 拱肋提升至设计位置，架设卷扬机、安装拱肋合龙段，拆除卷扬机；⑧ 安装拱肋吊杆结构，拆除施工临时结构，调整边墩支座至设计标高。

经研究发现：在钢桁梁拱桥的施工阶段中，钢桁梁和拱肋大部分时间处于悬臂状态，此时钢桁梁和拱肋的部分杆件承受较大的压力，在施工过程中易发生失稳破坏。因此，必须对钢桁梁柔性拱桥几个容易发生失稳的施工阶段进行线弹性稳定分析，以掌握其稳定性，保证结构施工时处于安全状态。对该钢桁梁柔性拱桥进行6个关键施工阶段的弹性稳定性，各个计算施工阶段的稳定系数如图3所示。在图3中，横坐标数字表示施工阶段的某个关键时期，如：1表示施工阶段钢桁梁中跨合龙前；2表示施工阶段钢桁梁中跨合龙后；3表示施工阶段在钢桁梁上拼装拱肋安装；4表示施工阶段在钢桁梁上中跨两侧拱肋安装；5表示施工阶段拱肋提升至设计位置，架设卷扬机、安装拱肋合龙段，拆除卷扬机；6表示桥梁处于成桥阶段(计入二期和正常风荷载)。

从图3中可以看出，有限元软件ANSYS和MIDAS计算的各个施工阶段钢桁梁柔性拱桥的

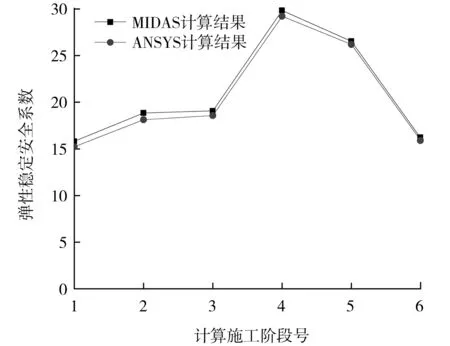
图3 施工全过程弹性稳定安全系数Fig.3 The safety factor of elastic stability in the whole process of the construction

线弹性稳定性安全系数比较相近，表明了该模型计算结果的真实性。从图3中还可以看出，桥梁结构在钢桁梁和拱肋的悬臂施工阶段，结构的安全系数发生了明显的变化，经历了一个由逐渐增加再到减小直至平稳阶段的过程。但是，各个施工阶段的弹性稳定系数均较大。表明：在施工过程中，结构具有较高的稳定性。其中，在钢桁梁中跨合龙前计算施工阶段的稳定安全系数最小。产生该现象的原因是主跨跨中2个临时墩距离较远，钢桁梁的悬臂最长，钢桁梁截面中轴以下的杆件容易受压失稳。在钢桁梁上拼装中跨两侧拱肋计算施工阶段的安全系数最大(即该结构最安全)，此时正处于钢桁梁合龙后且拱肋中间部分由提升塔吊起，因此，梁上承担荷载最小，相应杆件的应力也较小。最危险施工阶段在主跨钢桁梁合龙前，失稳模态如图4所示。

图4 钢桁梁合龙前的失稳模态Fig.4 Instability mode of steel truss beam before closure

分析结果表明：虽然桥梁结构各个施工阶段的整体稳定性安全系数较高，但是如果结构的单个杆件承担荷载过大而屈服，也会造成结构的局部失稳，影响整个桥梁的稳定性。钢桁梁中跨合龙前施工阶段的结构稳定安全性最低，因此，研究该阶段结构重要杆件的单杆稳定性，加强局部稳定性，对提高整个结构的稳定性显得尤为重要，各个杆件的应力情况和稳定安全系数见表1。

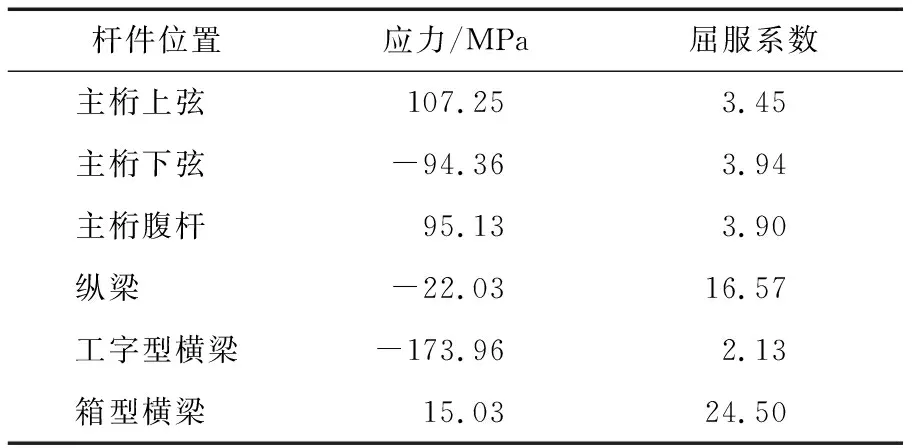
表1 施工荷载下受力最不利杆件Table 1 The most unfavorable members under the construction load

注：拉应力为正值，压应力为负值。

从表1中可以看出，在钢桁梁中跨合龙前的施工阶段，支座处工字型横梁的应力最大为173.96 MPa，钢桁梁主桁上弦杆次之，而箱型横梁的应力最小为15.03 MPa。其原因是：钢桁梁处于大悬臂状态，支座处受到弯剪组合应力最大，主桁上弦和下弦受到较大的拉力和压力。在线弹性情况下，结构的应力随着荷载的增加而线性增加。若将杆件应力达到屈服时的系数作为承载力系数，工字型横梁的屈服系数最小为2.13，单根杆件的屈服系数远小于结构整体的稳定安全系数。

3.2 运营阶段线弹性稳定承载能力和最不利杆件分析

为了解在实际运营期间不同荷载工况下钢桁梁柔性拱桥的稳定性，采用有限元软件ANSYS和MIDAS，对结构有可能存在的10种荷载布置方式进行了合理模拟，计算了相应的线弹性承载力和失稳模态。在考虑桥梁施工工序对成桥阶段的受力影响后，通过恒载和活载同时增加的方法，对钢桁梁柔性拱桥的特征值进行了分析。在ANSYS的计算中，将荷载不断增加直至一阶模态对应的特征值为1，此时的荷载为临界荷载{F}cr。线弹性下各工况稳定安全系数见表2。

从表2中可以看出，桥梁的稳定安全系数采用ANSYS和MIDAS软件计算的结果一致，表明计算结果可信度较高。在各个荷载工况下，结构的弹性稳定安全系数较高，即结构的稳定性较好。其中，恒载+隔跨活载的情况下，结构的弹性稳定安全系数最低，但该种工况在实际铁路桥梁运营中出现的概率相对较低；其次为恒载+主跨活载工况，安全系数为10.61，屈曲模态如图5所示。结构的前五阶屈曲形式全部为拱肋的整体屈曲。

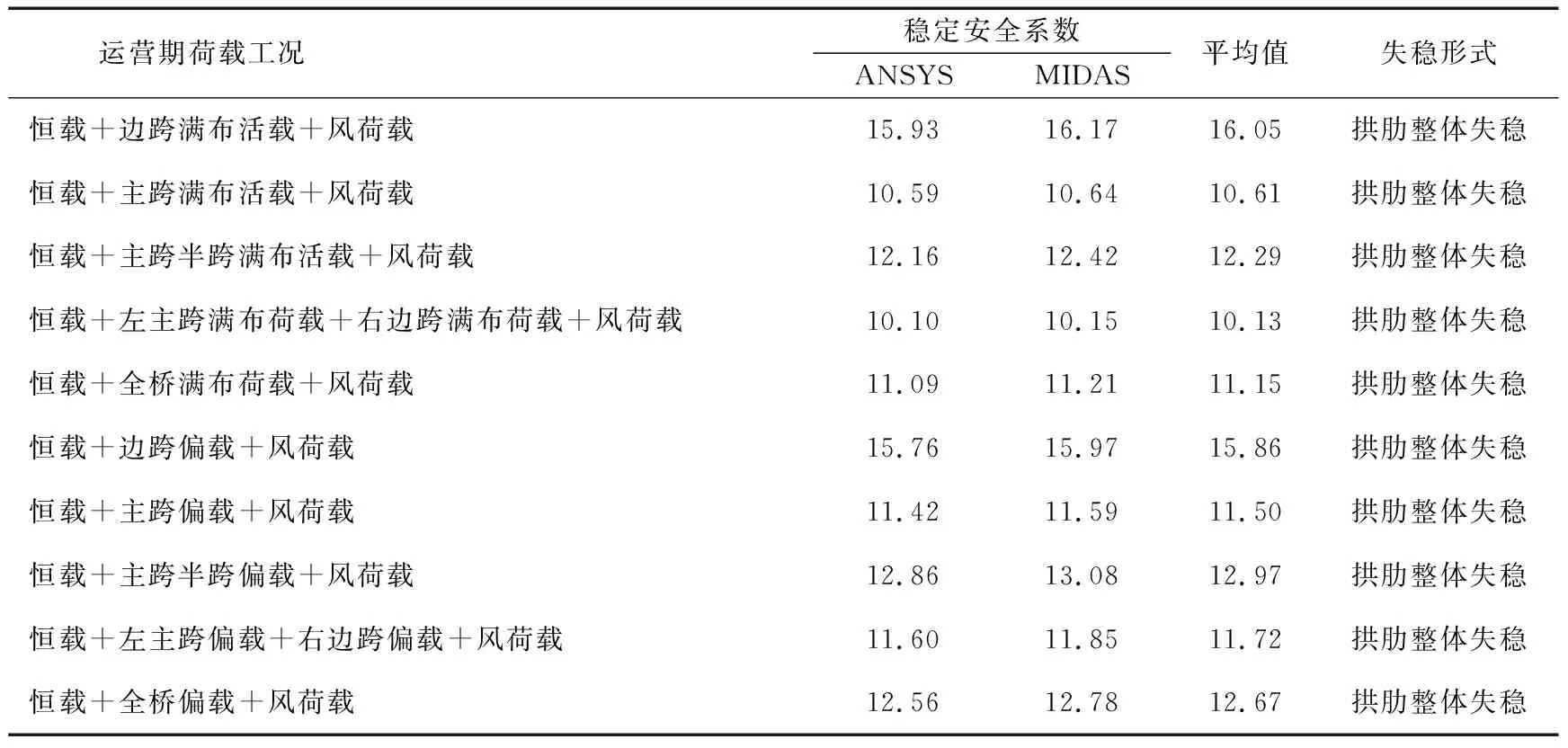
表2 钢桁梁柔性拱桥运营阶段线弹性稳定安全系数Table 2 Linear elastic stability safety factor of steel truss girder flexible arch bridge in the operation stage

注：平均值为ANSYS和MIDAS计算结果的平均值。

图5 ASNYS第一阶屈曲模态Fig.5 First order buckling mode in ANSYS software

在模拟了桥梁结构的所有运营荷载情况后，使用MIDAS提取出结构各种杆件中受力最不利的单元，同时，使用移动荷载追踪器，找到每种杆件达到最不利状态时的活载布置方式。其中，桥梁结构在设计荷载下受力最不利杆件的应力见表3。从表3中可以看出，拱肋部分和主桁腹杆的应力相对较大，而主桁上、下平联及横撑的应力相对较小。同样，若将杆件应力达到屈服时的系数作为承载力系数，屈服系数最小的为主桁斜腹杆，仅为2.06。

表3 设计荷载下受力最不利杆件Table 3 The most unfavorable members under the design load

4 结论

通过有限元软件ANSYS和MIDAS对某钢桁梁柔性拱连续梁桥的各个施工阶段和运营期不同的荷载形式进行详细的数值模拟和计算分析，得到结构弹性稳定能力的结论为：

1)由线弹性稳定的计算对比分析可知，ANSYS模型的稳定安全系数结果与MIDAS模型的结果相符。在各个施工阶段和运营阶段，某钢桁梁柔性拱连续梁桥的线弹性稳定安全系数都较高，施工阶段中跨钢桁梁合龙时结构的稳定安全系数最低为15.92，运营阶段列车荷载为隔跨满载分布时结构的稳定安全系数最低为10.13，表明桥梁结构在建设和运营时期都能保证较好的稳定性。

2)通过对桥梁结构施工阶段的计算分析，表明：在钢桁梁和拱肋的悬臂施工阶段，结构的安全系数发生明显变化，经历了一个由逐渐增加再到减小直至平稳阶段的过程；临时支撑对结构保持稳定状态尤为重要，在钢桁梁的架设初期和末期应加强安全措施。

3)在桥梁结构运营期间，列车荷载为主跨满载时，钢桁梁柔性拱桥杆件的受力最不利。设计荷载下结构杆件受力最大的为拱肋及主桁上弦杆和斜腹杆部分，将杆件应力达到屈服时的系数作为承载力系数，其值最小为2.06。

4)钢桁梁拱桥的线弹性稳定安全系数介于10.127～16.051之间，均为拱肋的整体失稳破坏；结构整体的稳定系数比最不利杆件的屈服系数大，表明桥梁结构的稳定承载力远大于杆件强度承载力。