高功率激光谱合成系统中热效应的分析
阴素芹,陈立功
(重庆理工大学 电气与电子工程学院, 重庆 400054)
高功率激光被广泛应用到材料加工、激光医疗、激光雷达遥感空间通信和高能武器等领域,因此,如何得到高功率的激光输出,成为了人们关注的焦点[1-3]。谱合成作为非相干合成技术的典型代表,利用色散元件对光纤激光器阵列单元输出的不同波长的激光束进行远场和近场的光束叠加,且合成光束的光束质量几乎与单根光纤激光器的光束质量相近[4-6]。
体布拉格光栅具有很好的热稳定性、光学稳定性和机械稳定性,且在可见到近红外光谱区域有良好的角度和波长选择性,从而成为高功率光纤激光器谱合成系统的理想色散元件[8],但是随着激光能量的不断提高,当强激光辐照在体布拉格光栅时,部分能量被体布拉格光栅所吸收,从而在体布拉格光栅内产生温度梯度,导致布拉格光栅的表面产生形变,并且光学材料形变和激光的功率密度、光斑尺寸、光强分布以及光学材料的物理参数有关。本论文主要针对不同高功率激光导致体布拉格光栅产生形变,研究当激光束经有形变的体光栅反射以后,光栅的形变对谱合成系统合成光束的光强和光束质量M2因子产生的影响。
1 基于体布拉格光栅的外腔谱合成系统
图1给出了基于体布拉格光栅的外腔谱合成系统的物理模型,针对高功率光纤激光器谱合成系统中体布拉格光栅存在的热效应问题,利用光束非相干叠加原理,讨论分析基于有形变的体布拉格光栅谱合成系统合成光束的传输特性。
在谱合成系统中,利用4个体布拉格光栅来实现5路光纤激光器的谱合成,其中每个体布拉格光栅只对满足布拉格条件的激光束进行完全反射,而对照射到光栅表面的其他的激光束进行完全透射,控制几束激光束的出射方向相同,就可以实现空间的叠加。
2 体布拉格光栅的热效应
随着谱合成系统激光器输出能量的不断提高,当强激光辐照在体布拉格光栅时,部分能量会被体布拉格光栅所吸收,从而在其内产生温度差,当温度差达到一定的值,布拉格光栅的表面就会发生形变,其原理如下:
布拉格光栅采用端面泵浦,泵浦光的光强分布为[9]:
I=I0exp(-αz)
(1)
式中:α是体布拉格光栅的吸收系数;z是激光的传播距离;I0是在垂直z方向的x-y平面内的光强分布,激光加热函数的空间分布采用高斯分布[10]。
(2)

当泵浦光传输dz距离后,损失的光能为晶体吸收的光能,即
dI=I0αexp(-αz)dz
(3)
假设转化为热的部分光能占总吸收的泵浦光能中的份额为η,可得到体布拉格光栅的热源为:
Q=αηI0exp(-αz)
(4)
其中体光栅对激光束的吸收为α=0.002 cm-1,体光栅对激光束的透射效率为η2=0.96。根据以上理论,用ANSYS有限元软件[11-12]对不同高功率激光导致的体光栅的温度场和应变场进行模拟仿真。
3 光栅热效应对谱合成系统传输特性的影响
当波长λi的激光束在有形变体光栅中传输时,其光场分布应满足波动方程[5,11]:
(5)
式中:k1=2π/λ1为波数;εi为有形变时体光栅介质的介电常数,可表示为[13-14]:
δniT(x′,y′)
(6)
式中:δni为折射率调制的幅度;δniT为背景折射率的变化;Λi(x,y)为有形变体光栅的周期;eiq为体光栅的栅线方向,其中体光栅的背景折射率nav= 1.486 7,折射率调制的振幅δn= 1.25×10-4。
εi≈(niav+δniT)2+2(niav+δniT)·

(7)
考虑光栅的热效应导致的形变,当波长λi的激光束经光栅反射后,由光栅形变引起的相位因子:
σ=exp{-iki[L(0,0)-L(x′,y′)]/2}
(8)
5束激光经有形变的布拉格光栅反射,波长为λi的光纤激光在光栅中的光场为:
(9)
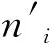

图2 体布拉格光栅形变的示意图
当体布拉格光栅发生形变以后,体布拉格光栅的布拉格条件可表示为:
(10)

将式(7)和(9)代入式(5),并满足布拉格条件式(10),可得到入射和反射光束光场所满足的耦合方程组:
(11)

将体光栅进行分片处理后,采用有限差分Crank-Nicholson和稀疏矩阵方法,通过反复迭代对方程(11)进行数值求解。相应的初始条件为:
(12)
考虑到体光栅的表面形变引入的相位因子,波长λi的激光束经有形变的反射式体光栅反射后的输出光场分布可表示为:
xcosθin+z0]+ikφ(xcosθin+z0)}}
(13)
那么波长λi的激光束经有形变的反射式体光栅体布拉格外腔式谱合成系统以后,在谱合成系统最后一个体布拉格光栅输出面上的光强分布可表示为:

(14)
式中:ρ、ζ为体布拉格光栅的透射系数和吸收系数;N为谱合成系统中的体布拉格光栅的个数。
根据非相干叠加的原理[14],N+1束激光束被N个体布拉格光栅谱合成以后在谱合成系统最后一个体光栅输出面上的光强分布为



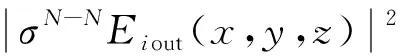
(15)
光束质量是评价谱合成系统好坏的一个重要指标,本文用M2因子来计算合成光束的光束质量,其光强二阶矩[15-17]可表示为:
(16)
4 数值计算与分析
用公式(13)和(15)计算5束光纤激光经有形变的体光栅谱合成后,其合成光束在近场光强分布和光束质量M2因子。计算所用参数[18]:入射激光束的波长分别为λ=1.064 μm,波长之间的间隔为0.4 nm,束腰宽度w0= 3.5 mm,光栅的厚度为L0= 2.5 mm,光栅的频率f=2 200/mm,体光栅的热折射系数αn=3.44×10-8/℃。体光栅的密度ρ=2.65 g/cm3,线性热膨胀系数αl=0.27×10-6/℃,体光栅的比热c=9.66 J/(kg·℃)。
图3和图4中(a)P=500 W,(b)P=1 000 W,(c)P=1 500 W不同功率的高斯光束激光辐照下体布拉格光栅的温度场分布和应变场分布,由图3和4可以看出,当相同光斑尺寸高斯激光束辐照体布拉格光栅材料时,功率越高,激光的功率密度就越大,光斑中心温度最高,边缘形成了很大的温度梯度。并且随着激光能量的增大,体布拉格光栅材料的中心温度升得越快,温度梯度也变得越来越大。激光的功率密度越大,温度梯度也越来越大,由温度梯度造成的体布拉格光栅的形变也越大。
把ANSYS软件模拟出来的光栅形变的数据导入Matlab软件,数值计算光栅热效应对谱合成系统光束传输特性的影响。图5给出了5束不同波长的激光通过不同形变的体布拉格光栅反射以后,输出光束的光强分布和M2因子。

图3 不同功率的高斯光束激光辐照下体布拉格光栅的温度场分布

图4 不同功率的高斯光束激光辐照下体布拉格光栅的应变场分布
从图5可以看出,5束光纤激光经体布拉格光栅进行谱合成后,合成光束的光强分布的最大值随着光栅形变的变大逐渐减小。进一步分析图5可知,随着光栅形变的增大,合成光束的光强分布形状有不规则的调制,光栅形变对合成光束光强分布形状的影响越来越大,即光强分布的畸变越来越大。

图5 合成光束的光强分布
M2因子是评价光束好坏的一个重要参数,图6给出了在谱合成系统最后一个体布拉格光栅输出面处合成光束M2因子随光栅形变的变化。
从图6可以看出,合成光束的M2因子随着光栅形变的增大也明显增大。当体光栅无形变时,合成光束的M2因子为1.05。但是当体光栅的形变量为ΔL=1.2 μm,合成光束的M2因子4。从图6还可以看出,随着光栅形变的增大,合成光束的光束质量变差。在谱合成系统中要求合成光束的光束质量几乎与单根光纤激光器的光束质量相近,因此在谱合成系统应控制体布拉格光栅的形变,以实现高功率高光束质量的激光输出。

图6 合成光束的M2因子随着光栅形变的变化
5 结论
当强激光辐照在体布拉格光栅时,考虑体布拉格光栅的热效应导致光栅的产生形变,基于热传导微分方程,用有限元方法分析了高功率高斯辐照下体布拉格光栅的温度场和应变场的分布。在此基础上,利用波动方程计算了5束激光束经有形变的体布拉格光栅反射后的光束特性。研究结果表明,体光栅形变对谱合成系统的合成光束光强和光束质量影响很大,即高功率激光导致的体布拉格光栅表面的热形变不仅会导致合成光束的光强降低并发生畸变,而且还会使光束质量M2因子变得越来越大,光束质量变差。本论文的研究对谱合成系统的应用有一定的理论参考价值。

