轴向基础振动对缠绕式液压胶管沿程压力衰减特性影响

李 俊，杨忠炯,2，周立强，张高峰

(1.中南大学 机电工程学院，长沙 410083；2.中南大学 高性能复杂制造国家重点实验室，长沙 410083)

硬岩掘进机（TBM）在工作过程中会产生强烈的振动，振动沿胶管轴向分量会加剧液压胶管和管内流体边界摩擦互动作用，这样不仅会使流体不稳定性加剧且压力沿管长方向衰减加大。液压胶管在TBM液压系统中得到大量使用[1-3]，因此有必要研究强振动环境下胶管管内流体压力沿管长的衰减特性。

目前国内外对液压胶管的研究主要集中在胶管破损机理的研究，文献[4-5]分别研究了振动对缠绕式胶管和编织式胶管钢丝层级间应力分布的影响，进而分析振动对胶管寿命的影响；文献[6]分析了编织式液压胶管的编织层的螺旋角对汽车制动软管变形布局和疲劳寿命的影响规律；对压力沿管长衰减特性研究主要集中在其未受外界激振力作用的状态，文献[7]研究了多层卷绕管的临界雷诺数与湍流状态的关系，定义了液阻的概念并得到了曲率连续变化时弯曲管道压力损失的半经验计算公式；文献[8]提出了沿程损失的半解析模型，并得出当边界突然变化时沿程损失的变化规律；文献[9]用相似雷诺数法测定了室内阀溜水管的摩阻值。但是针对强振动环境下且考虑流固耦合特性时液压胶管内流体压力衰减特性的研究还未见到相关报道。本文将液压胶管看成是复合材料管，建立液压胶管两端固定且受轴向基础振动的流固耦合模型，推导出管道沿程压力损失的数值计算公式，并研究振动参数、结构参数、流体参数对强振动环境下压力沿管长方向衰减特性的影响规律，为TBM管系设计及抗振设计提供理论依据。

1 缠绕式液压胶管轴向流固耦合模型

1.1 缠绕式液压胶管的简化模型

液压胶管一般由内胶层、钢丝增强层、外胶层组成。液压胶管钢丝增强层可以看做钢丝和橡胶的复合层，其层数可以为单层、双层、四层等多种形式，取其单层板的厚度为钢丝的直径d，首先对单层板（见图1）进行研究，设缠绕方向为T，面内垂直于钢丝方向为L，单层板的法线方向为r，其结构模型见图1(a)；实际计算时用正方形代替钢丝的圆形截面，单层板简化模型见图1(b)。取单层板的部分为研究模型见图1(c)。

其长为b/2(b为两钢丝中心距)，宽度为d/2。图中1区为钢丝截面积的1/4，1代表钢丝，2、3、4区代表橡胶，其中1、2区组成I区域，3、4区组成II区域。I区域中钢丝、橡胶所占比例x、y分别为：x=；代表性体积单元中I、II区域所占比例：

根据复合材料力学中串并联型模型计算复合层单层板主方向上的工程材料常数[9-10]：

式 中 ：ET、EL、Er、μTL、μTr、μrL、GTL、GTr、GrL分 别为单层板主方向弹性模量、泊松比、剪切模量；Es、μs、Gs、Eru、μru、Gru分别为钢丝和橡胶的弹性模量、泊松比、剪切模量。

在材料处于线弹性状态情况下，其应力应变遵守Hooke定律，即

式中：[S]d为材料的柔度矩阵。根据单层板主方向的工程常数可得

图1 液压胶管单层板模型

在实际应用中，液压胶管受力一般沿着胶管的径向和轴向，那么必须对单层板刚度矩阵（T,L,r）进行坐标轴的转化得到偏轴刚度矩阵即转化为柱标系（Z,r,θ）（示意图如图2）。

图2 液压胶管柱坐标示意图

可知其刚度转化矩阵为

由图2可知其坐标转换角β等于钢丝的缠绕角α，奇数层(k=2n+1)取β=α,偶数层(k=2n)取β=-α，从而得到单层板的偏轴刚度矩阵

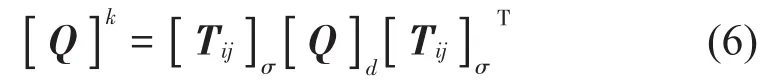
由于液压胶管内外层材料特性与复合层材料特性差异较大；经典的层板理论不适用于液压胶管整体弹性特性的推导。本文应用P.C.Chou[12]多层板宏观模量分析方法。

液压胶管的内外层橡胶为各向同性材料，可知

其刚度矩阵为

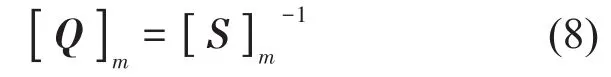
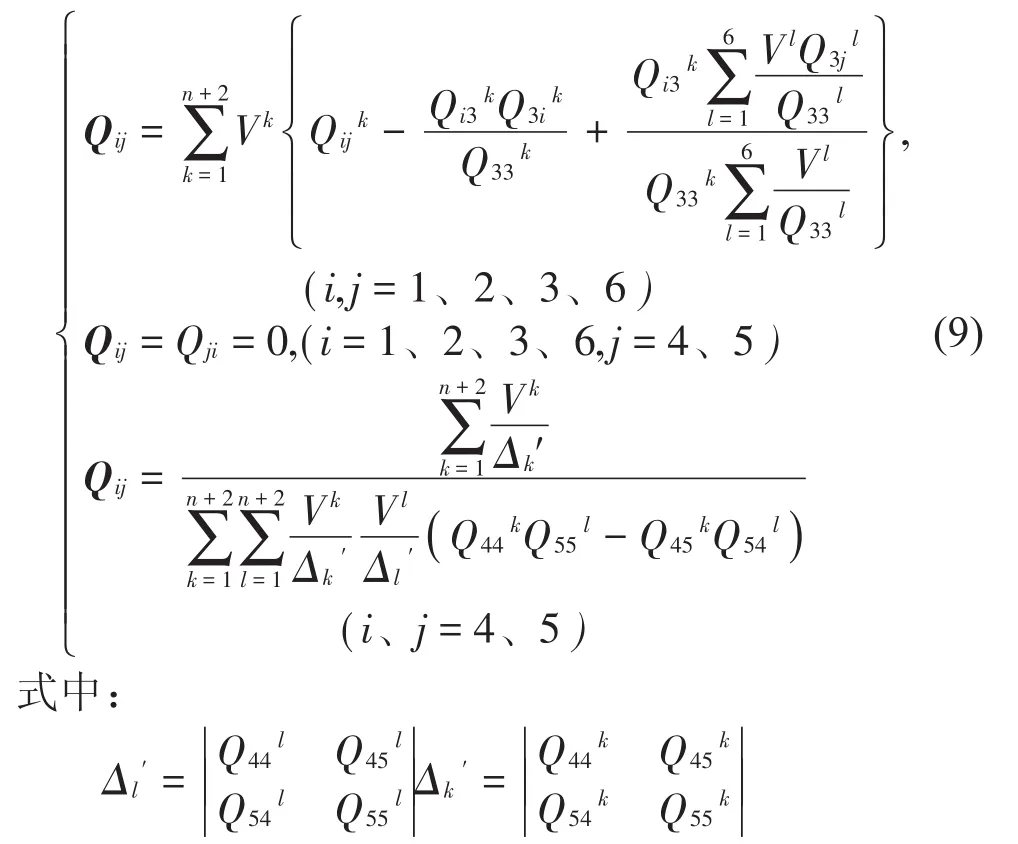
通过刚度矩阵求逆可得柔度矩阵，得到液压胶管的轴向弹性常数

1.2 缠绕式胶管轴向振动流固耦合模型

1.2.1 假设条件

(1)胶管内流体无内外热量交换；

(2)将液压胶管作为线性材料处理；

(3)模型中只考虑摩擦耦合和泊松耦合，忽略结构阻尼；

(4)仅考虑流体扰动沿轴向的变化且忽略径向惯性力；

(5)液压胶管安装在沿胶管轴向做简谐振动的基础上。其表达式为：A=A1sin2πft，A1、f为简谐振动的振幅、频率（理论模型见图3）。

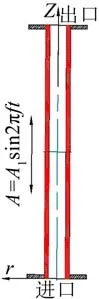
图3 理论模型

1.2.2 胶管轴向基础振动的流固耦合四方程模型

针对强振动环境下流体与液压胶管互动效应引起的边界摩擦耦合的研究，本文根据许多学者所采用的流固耦合四方程模型[13-14]（该模型得到众多学者的论证）和管路受迫响应相结合的理论，通过与四方程相似的推导，建立液压管路轴向基础振动的流固耦合模型，该控制方程由2个流体方程和两个液压胶管的方程组成，具体如式(11)至式(14)所示。

流体的轴向运动方程

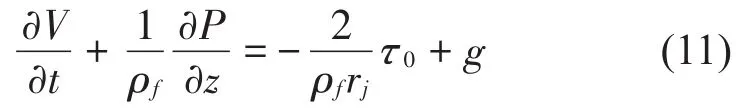
流体的连续方程

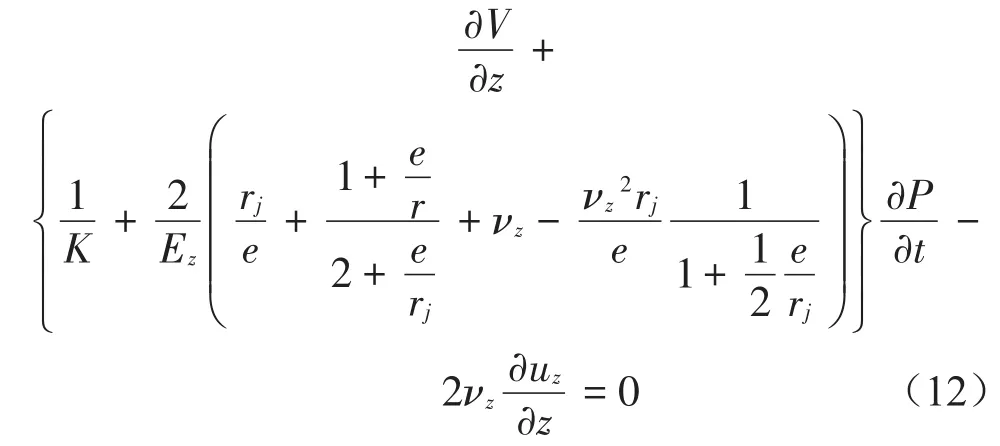
胶管的轴向运动方程

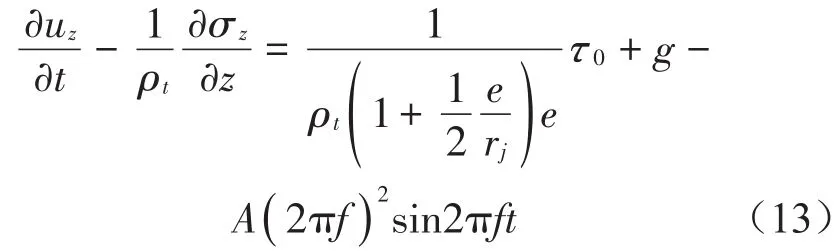
胶管的应力-位移的关系方程

式中：V、P分别为流体的流速和压力：uz、σz分别为胶管的轴向速度和轴向应力；e、rj分别为胶管的厚度和内半径；K为流体体积模量；ρf、ρt为流体密度和液压胶管的密度，λ为流体与胶管的摩阻系数。

2 数值仿真和实验模型分析

2.1 模型参数及初始条件

根据实际液压胶管在全断面硬岩掘进机的使用状况，选取液压胶管基本参数如表1所示。

表1 液压胶管参数

胶管材料由普通钢丝(Q235)和丁晴橡胶(NBR)构成，其参数如表2所示。

表2 材料参数

胶管内流体的初始流速V0=5 m/s，进口初始油压P0=10 MPa，液压油密度为890 kg/m3，液压油体积模量K=1 600 MPa，l为管长。

根据以上参数，初始时认定管道内液体具有恒定流速V0，管道两端固定则管道的轴向速度为基础振动的速度，忽略四方程中与时间相关的量，并对各式在轴向上积分得到管道的初始条件为

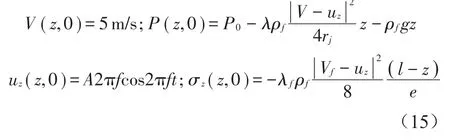
2.2 数值仿真模型

为了求解液压胶管管路中流体的压力和流速及胶管的轴向内应力和速度，采用有限差分法将管路分成n等分，在MATLAB/Simulink中将其表示为向量的形式

对于流固耦合模型中的∂(V,(V,P,uz,σz)/∂t用MATLAB/Simulink积分模块来表示。在MATLAB/Simulink中可以用Selector模块对向量进行重新排序，因此可以实现∂(V,(V,P,uz,σz)/∂z的运算。

将流速的边界条件v0和前n-1个计算单元流速组成新的向量形式如下

因此，∂V/∂z可以写成

同理将流体压力的边界条件P0、液压管路轴向运动速度和轴向应力的边界条件uz0、σz0和其n-1个单元的流体压力、轴向速度和轴向应力组成新的向量P'、u'z、σ'z。那么得到

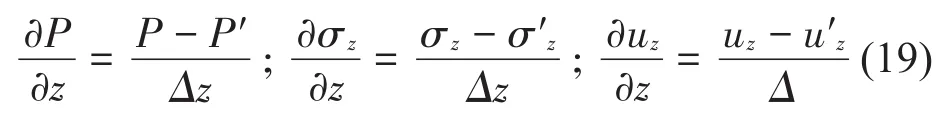
根据以上等效形式和流固耦合方程中各个表达式前的系数就能建立基础振动液压胶管的轴向流固耦合的MATLAB/Simulink仿真模型。

那么压力沿管长减小量，即沿程压力损失ΔP为

将以上参数和初始参数代入液压胶管的MATLAB/simulink流固耦合模型，并将管道分为20等分，仿真步长采用变步长，最大时间步长为0.000 1 s，通过仿真计算在振动参数、管道参数、流体参数变化时沿程损失的变化规律。

2.3 实验分析

实验装置由实验胶管、振动台、胶管固定支架、管夹、长管道试验台、溢流阀、压力传感器和Multi System 8050数字采集器组成，试验系统如图4所示。

图4 实验系统装置

实验中测得胶管进口初始压力为10 MPa、在振幅为3 mm～7 mm、频率为15 Hz～95 Hz的正弦振动载荷下的液压胶管进口压力P1和出口压力P2随时间的变化规律，那么沿程压力损失为P1-P2-ρfgl。

2.4 仿真、实验结果对比分析

在振幅为5 mm、频率为40 Hz时液压胶管沿程压力损失仿真和实验的结果如图5所示。

图5 仿真、实验结果对比分析

由图可知，仿真分析时沿程压力损失的变化范围为10.3 kPa～32.07 kPa，实验测得的沿程压力损失的变化范围为12.7 kPa～34.47 kPa，且都成周期性变化，实验测得的摩擦损失大于数值仿真分析，这是因为实际泵工作时出口有压力波动，长为1 mm的胶管局部有小的弯曲半径，造成流体与管壁冲击增大，沿程损失增大，但是两者的变化趋势是一致的，因此可证明仿真模型的可靠性。

3 系统参数对沿程压力损失的影响

3.1 振动参数对胶管沿程压力损失特性的影响

无基础振动和基础振动振幅为5 mm、频率为40 Hz条件下，胶管长度为1 m时的沿程压力损失特性如图6所示。

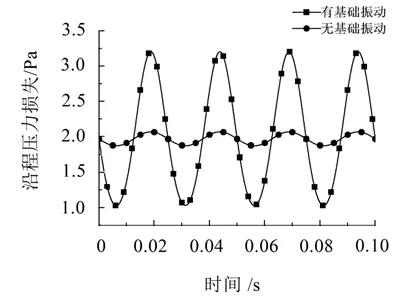
图6 有无基础振动时胶管沿程压力损失波动对比图

由图可知无基础振动时，沿程损失有波动情形，这是由于系统的自激振动引起的流体和胶管边界摩擦互动效应；有基础振动时，胶管的沿程损失峰值是无振动情况下的1.55倍，且沿程损失的波动明显加大，说明外界激振力加强了胶管与管内流体的摩擦耦合作用。

基础振动频率为40 Hz、振幅在4 mm～7 mm变化时，液压胶管沿程压力损失变化规律见图7(a)。由图可知，在振幅为4 mm～7 mm时，液压胶管沿程损失峰值分别为29.593 kPa、32.069 kPa、34.642 kPa、37.318 kPa，随着基础振动的幅值增大，液压胶管沿程损失波动幅值增大，且接近线性增加，振幅增加1 mm，波动幅值增加2.6 kPa。说明随着基础振动振幅的增加，胶管与流体摩擦耦合作用越强。

基础振动振幅为6 mm、频率为15到95 Hz时，胶管沿程损失波动峰值如图7(b)所示。

由图可知，在振幅为4 mm、5 mm、6 mm时，激振频率在15 Hz～95 Hz变化时，沿程损失的压力峰值变化范围分别为23.448 kPa～50.435 kPa、24.61 kPa～57.775 kPa、25.44 kPa～64.676 kPa，所以可以得知，随着激振频率的增加，液压胶管的沿程损失也随之增大，这是因为频率增加使传递的能量增加，加强了胶管与管内流体摩擦耦合作用。

3.2 结构参数对胶管沿程压力损失特性的影响

基础振动振幅为6 mm、频率为40 Hz的条件下，胶管长度在0.5 m到2 m时，液压胶管沿程压力损失变化规律见图8(a)。由图8(a)可知液压胶管的沿程压力损失的变化范围在胶管长度0.5 m、1 m、1.5 m、2 m 时分别为 4.461 kPa～17.322 kPa、8.922 kPa～34.645 kPa、13.383 kPa～51.968 kPa、17.844 kPa～69.291 kPa，可分析出压力损失均值分别10.892 kPa、21.784 kPa、32.676 kPa、43.568 kPa，由此可知振动条件下，随着胶管长度的增加沿程压力损失均值基本呈线性增长，而沿程损失波动比即是减小的，这是因为振源加在入口端，振动沿管长方向是一个能量衰减的过程，那么胶管与流体的摩擦耦合沿管长方向是减弱的。

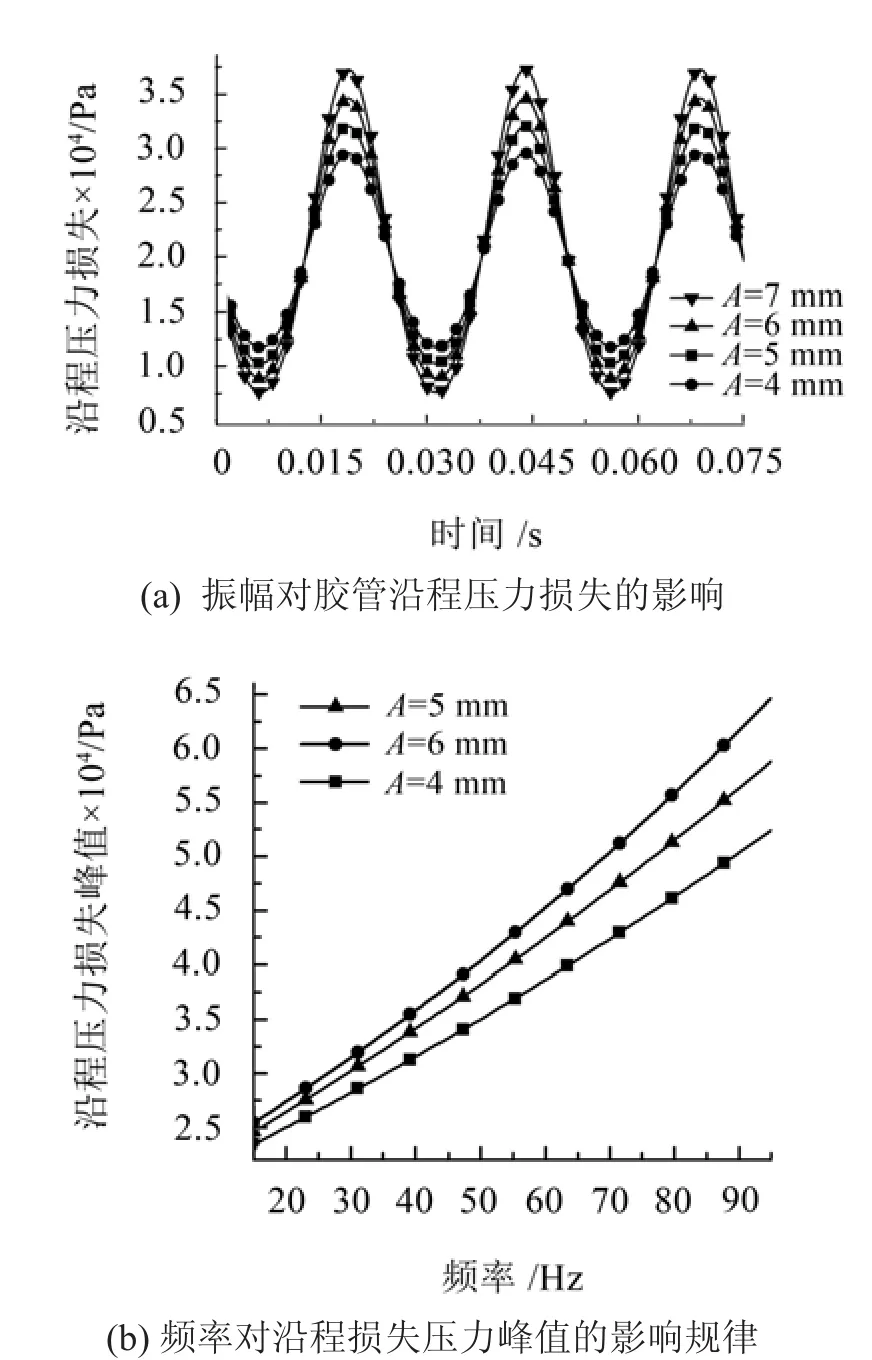
图7 振动参数对胶管沿程损失波动影响

在同样的振动条件下，胶管内径从10 mm变化到16 mm、考虑与不考虑摩擦耦合时液压胶管沿程损失峰值的变化规律见图8(b)，由图可知，在外界有激振力的条件下，考虑摩擦耦合作用时沿程压力损失大于不考虑摩擦耦合作用时的值，这说明摩擦耦合的作用加大了管内流体与胶管的互动作用。两种条件下，沿程压力损失峰值和波动比都随着胶管内径的增加逐渐减小，原因是流体域的增加使胶管与流体泊松耦合作用减弱，液压胶管传递到流体的振动能量减弱，从而导致胶管与流体边界摩擦互动效应减弱。

3.3 流体参数对沿程压力损失特性的影响

基础振动频率为40 Hz、振幅在4 mm～6 mm条件下，初始流速在3 m/s～5 m/s时，液压胶管沿程压力损失波动比变化规律见图9(a)。

由图9(a)可知，在振幅为4 mm～6 mm条件下，流体初始速度在3 m/s～5 m/s变化时，沿程压力损失的波动比分别在0.39～0.31、0.43～0.34和0.45～0.37范围内变化，由此可知随着流速的增加，沿程压力损失波动程度减弱，流体域稳定性增强，这说明随流体流速增加，胶管和流体的摩擦耦合作用程度减弱。

在同样的振动条件下，液压油为32号、46号、68号时，液压胶管沿程损失压力波动比如图9(b)所示（λ为不同液压油的摩阻系数）。

由图可知，当基础振动条件相同时，不同液压油的沿程损失压力波动比几乎不变，说明液压油黏度在振动条件下对流体与胶管的摩擦耦合作用的影响很小。

图8 胶管结构参数对沿程压力损失影响

4 结语

(1)基础振动会明显加强胶管与流体边界的摩擦耦合作用。

(2)振动条件下，沿程损失的波动幅值随振动幅值呈线性增长，振幅每增加1 mm，波动幅值增加2.6 kPa，沿程压力损失峰值随着振动频率的增大而增大。

(3)液压胶管管长对压力沿胶管衰减特性的影响大于胶管内径。

(4)流速增大时，沿程压力损失波动比减小，流体黏度对沿程压力损失波动的影响较小。

图9流体参数对沿程压力损失影响