基于熵权的模糊综合评价法在学习质量评价中的应用

蔡志荣

摘  要： 课程是学校内涵建设的核心内容，课程质量的评价对于课程建设起到决定性作用，评价课程的教学质量时，学生学习质量是最重要指标，也是最关键指标。学校常用考试成绩来衡量，是不全面和不准确的。文章基于模糊数学理论，采用熵权法对学习质量评价指标赋权，构造基于熵权的模糊综合评价模型，为课程建立客观科学的学习质量评价方法。

关键词： 熵; 模糊综合评价; 学习质量评价; 模糊数学

中图分类号：O236          文献标志码：A     文章编号：1006-8228（2018）12-75-03

Abstract： Curriculum is the core content of school connotation construction. The evaluation of curriculum quality plays a decisive role in curriculum construction. To evaluate the teaching quality of a course， students' learning quality is the most important index and the most critical index. It is not comprehensive and inaccurate to measure with the examination results， which schools commonly uses. With the theory of fuzzy mathematics， this paper uses entropy weight method to weigh the evaluation index of learning quality， constructs a entropy weight based fuzzy comprehensive evaluation model， and establishes an objective and scientific evaluation method for learning quality of curriculum.

Key words： entropy; fuzzy comprehensive evaluation; learning quality evaluation; fuzzy mathematics

0 引言

學校的硬件设施建设越来越先进，而学校的内涵建设成为发展的关键，课程建设是内涵建设的基础和核心。学生学习质量是衡量课程建设成败的最重要指标。需建立科学地评判学生学习质量方法，分析和总结评判结果，进而改善教学方式和方法，提升教学效果。决定课程学习质量的因素众多，以往常用考试成绩来衡量，是不全面的，不准确的，如何以客观、科学地方法来评判课程的学习质量，成为一个研究课题。

本文将以C语言程序设计课程为例，利用模糊数学理论作为依据，运用基于熵权法的模糊综合评价法来评价学生课程学习质量情况，可以评判出每位学生学习质量和班级整体评价。

1 模糊综合评判法和熵权法

模糊综合评价法19世纪60年由美国科学家扎德教授创立，如今已成为一种被广泛和有效应用的模糊数学方法，其方法以模糊数学、模糊统计法作为基础，分析并综合考虑影响事物决策或评价的各个因素（指标），量化所有不易定量或边界不清的因素，运用综合评价各因素计算得到评价结果的一种方法[1]。

好处：利用了量化手段来处理信息模糊的评价对象，运用计算得到比较客观、合理、科学、贴近实际情况的量化评价;

不足之处：综合评价法中指标权重矢量的确定方法随意性和主观性较强。

在信息论中，熵值反映的是信息的无序化，可以通过度量信息量的大小来决定对决策的作用，例如某指标所携带信息越多，越可以代表对决策的作用越大。熵权是综合分析、考虑各指标所提供信息量，根据信息量计算各指标权重的数学方法。

针对模糊综合评价指标权重多根据专家意见和经验得到，评价中随意性和主观性较强，不利于客观反应，结合熵权法来决定各指标的权重更为科学客观。

2 熵权模糊综合评价模型构建和应用

数据采集和处理：以某校软件专业在OJ系统中学习《C语言程序设计》课程数据为例，课程评价采用每个学生的期末成绩、态度成绩、OJ系统提交指标值、OJ系统正确提交指标值数据进行评价。

OJ系统：一个在线的黑盒判题系统。用户可以在线提交程序源代码，系统对源代码进行编译和执行，并通过预先设计的测试数据来检验程序源代码的正确性。本校《C语言程序设计》课程以OJ系统为平台进行教学。

期末成绩：期末考试所得成绩。

态度成绩：学生学习态度情况的评价，态度情况包括：日常考勤、上课纪律、课堂反应、课后学习情况等方面评价。

OJ系统提交指标值：根据系统中提交的次数所得分值，计算方法：每提交0.25分，得分不超过100，若超过100分，则以100分作为数据。

OJ系统正确提交指标值：根据系统中题目正确提交次数所得分值，计算方法：每正确量0.3分，得分不超过100，若超过100分，则以100分作为数据。

模型建立与求解主要步骤。

⑴ 根据评价目的确定评价因素集合U={u1，u2，…，un}，因素是参与评价的n（n=4）个因子的数值指标，指标：期末成绩u1、态度成绩u2、提交指标值（OJ系统）u3、正确提交指标值u4。

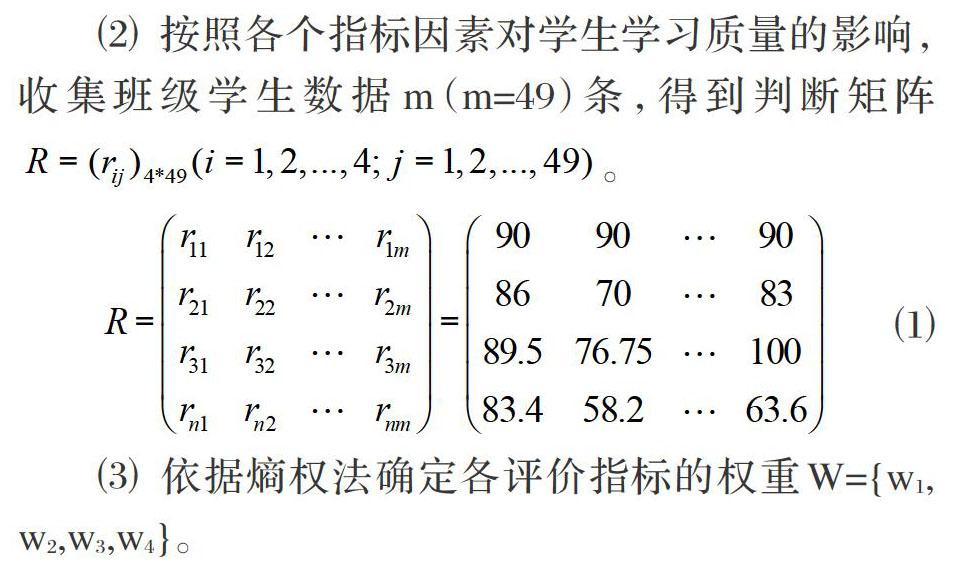
⑵ 按照各个指标因素对学生学习质量的影响，收集班级学生数据m（m=49）条，得到判断矩阵。

⑶ 依据熵权法确定各评价指标的权重W={w1，w2，w3，w4}。

① 将判断矩阵R进行标准化，得到标准化矩阵B，如图2所示。B的元素为：

其中，ri（min），ri（max）分别为同一指标值的最小值和最大值，通过上述转换，必满足，最大值为1，最小值为0，根据式⑵，计算得到标准化后指标数据如下。

由式⑷计算得到各指标的熵，如表1所示。

由式⑼计算各被评价对象的模糊综合评价结果如下：

⑸ 结合加权平均原则评价出班级综合评价。

加权平均原则：將等级看到一种相对位置，并使其连续化。为了能定量处理，运用“1，2，3…，m”来表示各等级，也可以称其为各等级的秩。通过对cj降序排序，得到的各代号的名次作为等级的秩。

由式⑽计算得到A=22.55，表示全班综合评价值达到并超过班级第23名学生的综合评价值，第23名的综合评价值：80.19。

3 结果分析

利用熵权法计算得到各项指标的权重数据分别：期末成绩0.120、态度成绩0.265、提交指标0.295、正确提交指标0.320，发现对期末考试在综合评价中起到的作用最低，权重的指标最大的正确提交指标值和提交指标值，这些指标对学生的学习质量评价更加准确和客观。

4 结束语

学生课程学习质量评价是一个复杂的系统评价工程，需要统筹并兼顾多个指标，评价标准与手段因对评价对象认识的广度与深度不断改进。本文运用信息论中熵权思想的课程综合评价，建立基于熵权的模糊综合评价法模型。以某校软件专业学生C语言程序设计课程数据作为样本，分析样本数据，发现课程学习质量指标权重排序如下：正确提交指标>提交指标>态度成绩>期末成绩，该结果能较好的反映出学生真实的学习情况，以正确提交指标和提交指标为主要权重指标，可以得到学生平时练习和作业完成的程度，也真实得到学生知识掌握情况和学习质量。模型在决定权重的方法中减少随意性和主观性，整个评价过程简单、计算方便、结果合理，具备在同类课程的评价中得到推广。

参考文献（References）：

[1] 曾蓉，陈洪凯，李俊业.熵权模糊综合评价法在公路洪灾危险性评价中的应用[J].重庆交通大学学报（自然科学版），2010.29（4）：587-591

[2] 常瑞阳.基于熵权模糊综合评价的绿色建筑施工风险研究[J].价值工程，2015（19）

[3] 邹志红，孙靖南，任广平.模糊评价因子的熵权法赋权及其在水质评价中的应用[J].环境科学学报，2005.25（4）：552-556

[4] 鸿吉.模糊数学基础及算法[M].科学出版社，2005.

[5] 付钰，吴晓平，叶清，等.基于模糊集与熵权理论的信息系统安全风险评估研究[J].电子学报，2010.7：1489-1494

[6] 郭晓磊，弓虎军.熵权模糊综合评判在储层评价中的应用[J].陕西理工大学学报（自然科学版），2018.2.

[7] 胡艳娟，武理哲，王占礼等.云制造服务综合评价模型研究[J].长春工业大学学报，2018.3.

[8] 秦忠诚，陈光波，李谭等.“AHP+熵权法”的CW-TOPSIS煤矿内因火灾评价模型[J].西安科技大学学报，2018.2.