基于减小轴向力测量干扰的高精度测力天平研制

闫万方, 蒋 坤, 张 江

(中国航天空气动力技术研究院, 北京 100074)

0 引 言

应变天平依然是目前风洞试验中的核心测量设备之一，随着风洞试验技术的发展以及飞机、箭弹等精细化设计程度的提高，风洞天平的测量精度要求也越来越高。近年来，针对不同试验测量需求，国内外设计人员开展了相应的天平研制工作，并着重针对提高轴向力的测量精度进行了研究，研制了如大载荷容量/刚度[1-2]、大升阻比[3]、高精度轴向力测量[4]等天平，取得了不错的效果。对杆式应变天平而言，轴向力是最难测量的载荷分量，其原因一是轴向力元件设计需严格协调天平刚度、强度和灵敏度之间的矛盾，二是各载荷分量对轴向力有不同程度的干扰且多非线性，加剧了轴向力的测量难度[5-6]。国内外风洞机构在降低轴向力干扰、提高测量精度方面一直在进行着研究和探索，其中，熊琳等[7]针对小直径杆式天平较弱刚性导致轴向力干扰较大的问题进行了深入分析，并提出改进设计措施。史玉杰等[8]对“横Π型”轴向力结构的干扰特性进行了研究，提出了通过改进结构设计和贴片位置从而改善轴向力干扰的方法。另外，文献[9-10]对“I型”梁、“T型”梁等进行了结构优化设计，使得常规结构天平的轴向力干扰显著减小。上述研究通过结构优化设计一定程度上减小了轴向力的干扰，但效果有限。同时，对常规天平而言，力矩(包括My、Mz及Mx)对轴向力元件的干扰应变较大，只能通过惠斯通电桥部分消除，受轴向力应变片的敷贴位置影响较大；另外，天平各分量载荷作用在轴向力测量梁上的应力分布交错复杂，相对于天平的其他分量，轴向力分量的长期稳定性较差。

针对上述问题，研制一台较小轴向力测量干扰的六分量杆式应变天平，用于箭弹类、小展弦比飞机等的气动载荷测量，旨在提高天平的轴向力测量精度和长期稳定性。本文提出一种新的轴向力测量元件结构形式，并采用有限元设计方法对其进行优化改进和分析，最终使得天平各分量载荷对轴向力应变片敷贴位置处的干扰应变近乎为零，而无需通过电桥去消除；该设计还改善了天平各分量载荷作用在轴向力测量梁上交错复杂的应力分布状态，提高了天平轴向力的长期稳定性。在完成机械加工和贴片工作后，进行了静态校准和标模试验，进一步检验了新研制天平的测量精、准度等性能指标。

1 天平设计及优化

1.1 设计要求

基于中国航天空气动力技术研究院(CAAA)FD-12风洞的试验测量载荷需求，天平设计载荷如表1所示，其中轴向力X、法向力Y、侧向力Z的单位为(N),俯仰力矩Mz、偏航力矩My、滚转力矩Mx的单位为(N·m)。天平直径为32mm，有效长度约165mm。

表1 天平设计载荷(单位：N，N·m)Table 1 Design loads (unit: N, N·m)

1.2 设计方案

目前，杆式六分量应变天平大多是通过设置专门的轴向力测量元件来实现对轴向载荷的测量。轴向力测量元件的设计是天平设计的难点和关键，通过结构设计，尽可能地保证轴向力测量元件对轴向载荷分量敏感的同时，降低对其他载荷分量的敏感性，以减小对轴向力的测量干扰。本文综合考虑天平设计载荷、直径尺寸以及应变片敷贴难度等约束因素，将轴向力测量元件置于天平轴线上的设计中心位置，以尽可能的减小测量干扰，天平整体结构设计如图1所示。

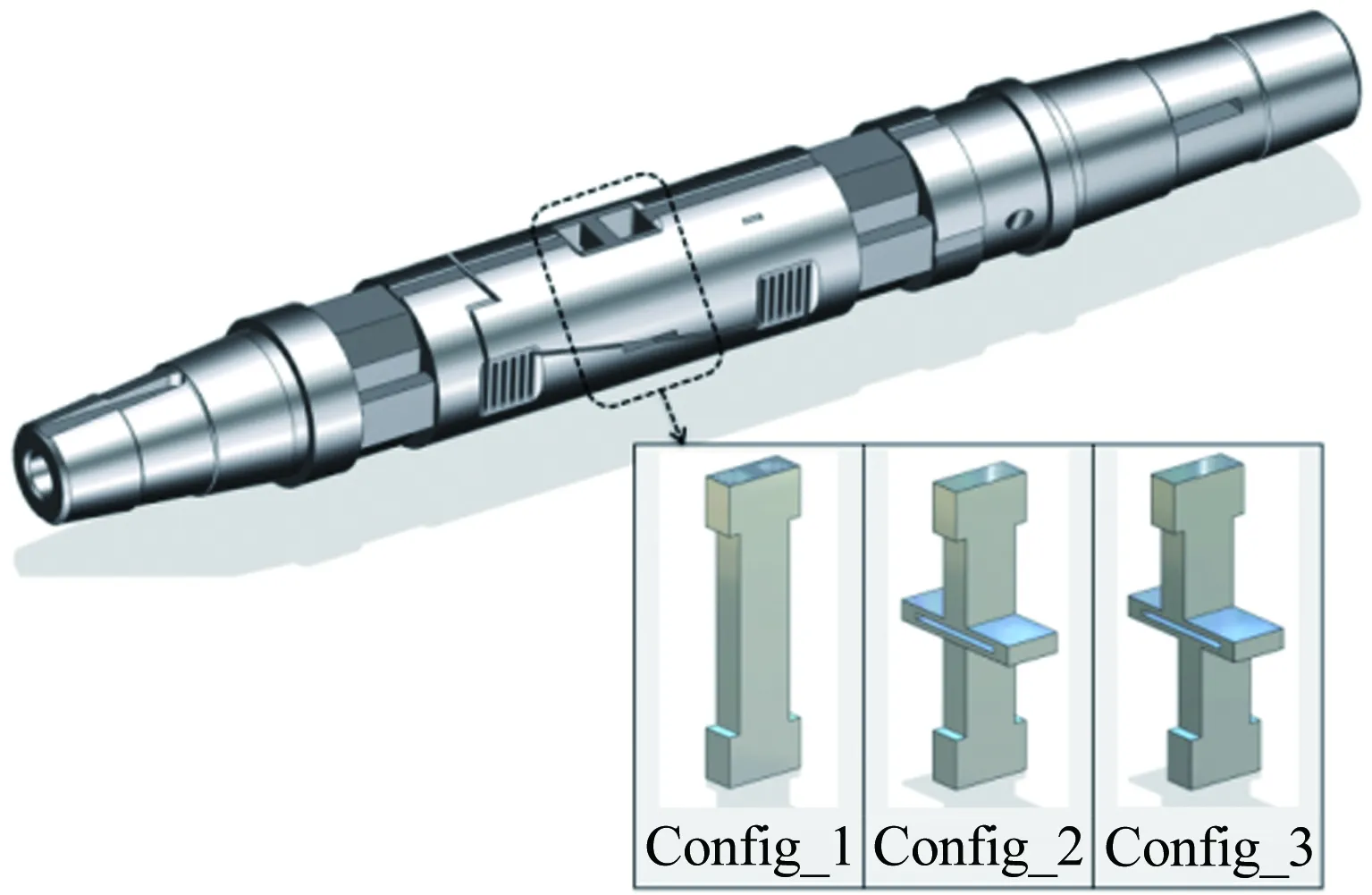
图1 天平整体结构及轴向力元件示意图

Fig.1Schematicdiagramoftheoverallconfigurationofbalanceandaxialforcemeasuringelementdesign

天平设计中，其他五分量测量元件采用常规结构设计，着重对轴向力测量元件进行优化和改进。如图1所示，采用有限元方法对比分析了3种结构形式轴向力元件的主应变输出和干扰特性，分别记为Config_1，Config_2和Config_3。其中，Config_1为“工”型结构，置于天平轴线上的设计中心位置，以彻底消除侧向及横向载荷(My、Z和Mx)对轴向力的应变干扰，测量梁通过两端的连接段与天平上、下框体连接，轴向受载时，测量梁发生双弯曲“S”型变形；Config_2在Config_1的基础上，在轴向力测量梁中间设置了铰链，削弱了测量梁的纵向刚度，并将其分为上、下2个部分，以减小纵向载荷(Mz、Y)对轴向力的应变干扰，轴向受载时两测量梁均发生单弯曲变形；Config_3在Config_2的基础上，将两测量梁沿天平轴线非对称设置，以消除由于天平结构自身非对称及局部刚度分布不均匀导致的纵向载荷(Mz、Y)对轴向力的应变干扰，轴向受载时变形方式与Config_2相同。通过对比分析和优化改进，本文采用Config_3作为最终的设计方案，其能保证在轴向力有足够的灵敏度前提下，使各载荷分量对轴向力分量干扰应变近乎为零，而无需通过电桥去消除，彻底解决了轴向力的测量干扰问题。

1.3 轴向力元件优化改进及分析

天平坐标系定义如图2所示，O为天平设计中心，轴向力测量元件则置于该设计中心位置；组合测量元件置于轴向测量元件的前后两侧，为常规三柱梁结构，用于测量其他五分量气动载荷。

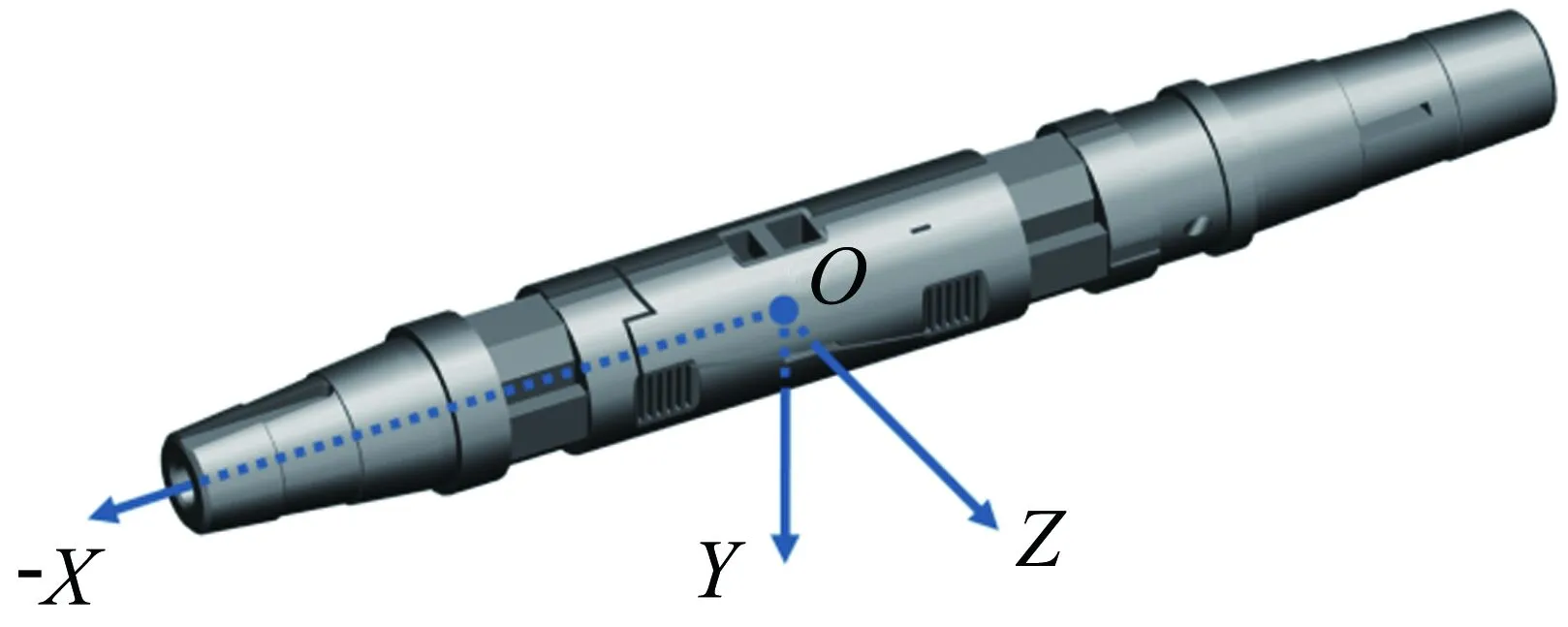
图2 天平坐标系定义

下面着重介绍轴向力测量元件的结构设计和优化改进，并对其干扰性能进行对比分析。图3和4分别为轴向力测量元件的应变片敷贴示意图和组桥定义，轴向力应变片R1～R4分别敷贴于测量梁根部的前后表面，并组成惠斯通电桥。表2所示为分别单独施加其他五分量设计载荷时，3种结构形式的轴向力元件在R1～R4贴片位置处的干扰应变输出。由表2可知，由于轴向力测量元件置于天平轴线上的设计中心位置，侧向及横向载荷(My、Z和Mx)对3种结构形式的轴向力测量元件干扰应变近乎为零。另外，Config_1受纵向载荷(Mz、Y)时，在R1～R4贴片位置处的干扰应变较大，且应变值不对称，这会导致电桥有较大的干扰输出；Config_2在Config_1基础上，在测量梁上增加了铰链，极大地削弱了测量梁的纵向刚度，从而使R1～R4贴片位置处的干扰应变显著减小，但应变值依然不对称；Config_3在Config_2的基础上将两测量梁沿天平轴线非对称设置，消除了天平结构自身非对称及局部刚度分布不均匀导致的干扰应变不对称问题，并进一步减小了纵向干扰应变。

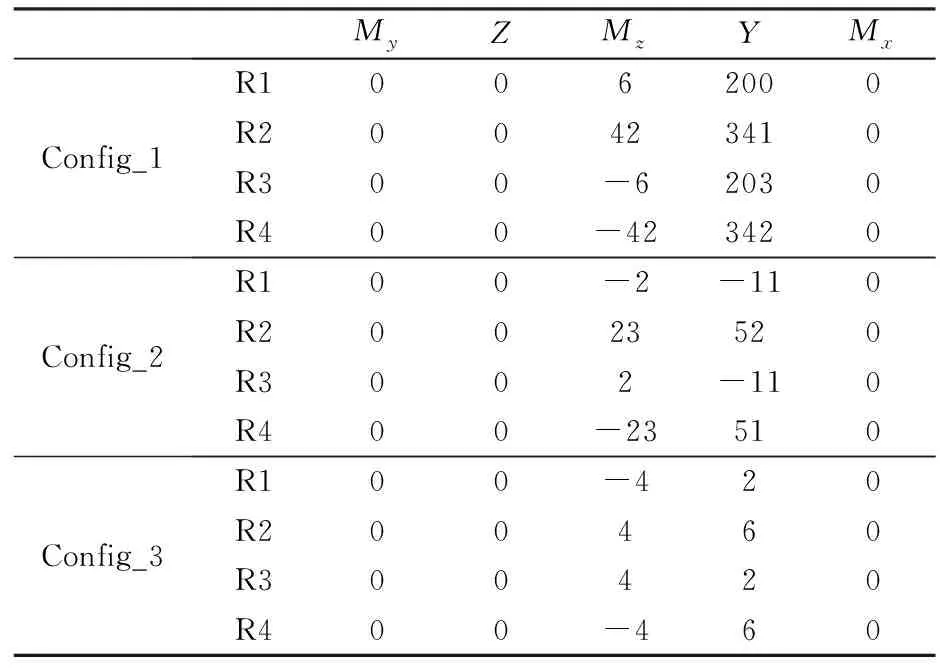
表2 各分量对轴向力元件的应变干扰(单位：με)Table 2 Interference strain output on axial component from the other aerodynamic forces (unit: με)

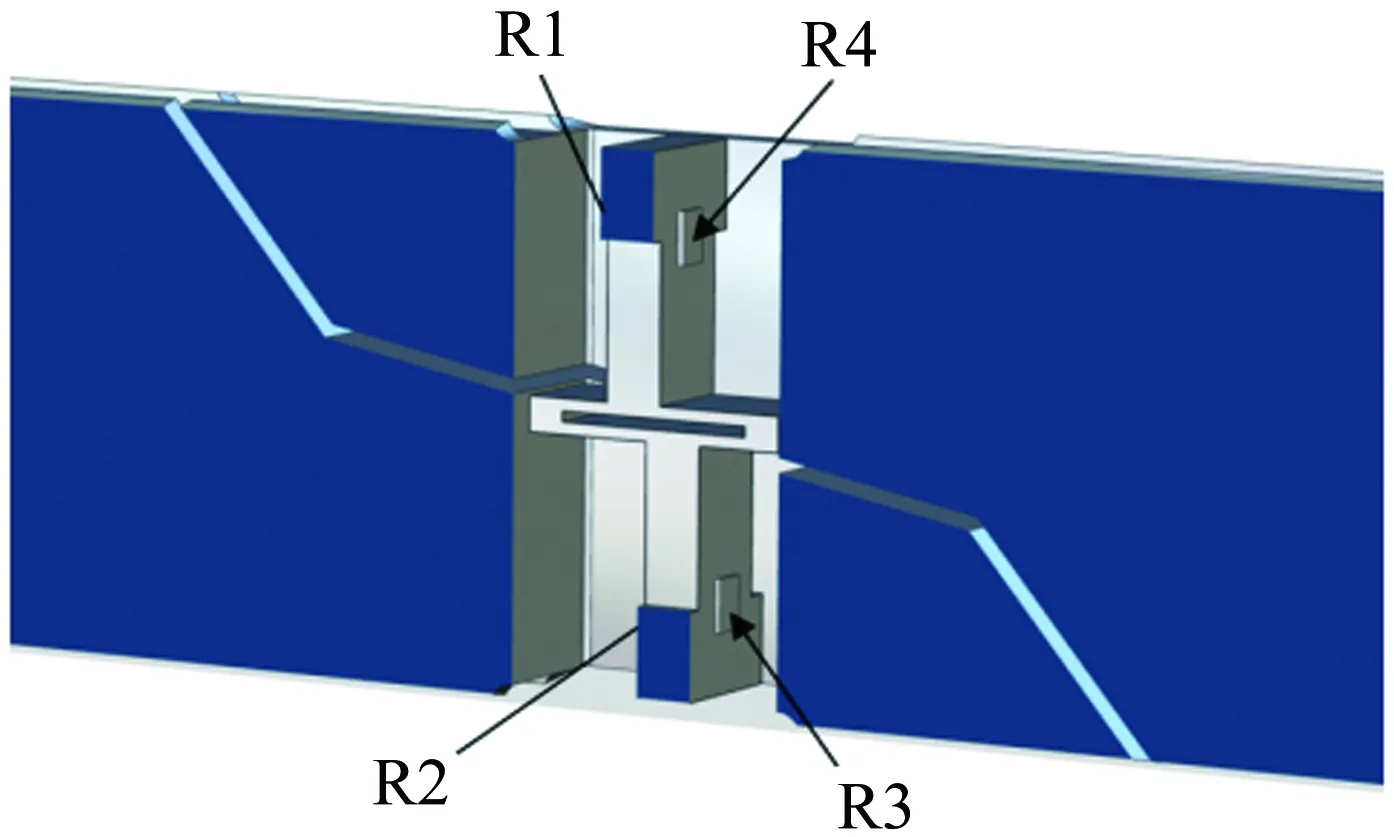
图3 轴向力测量元件的应变片敷贴示意图

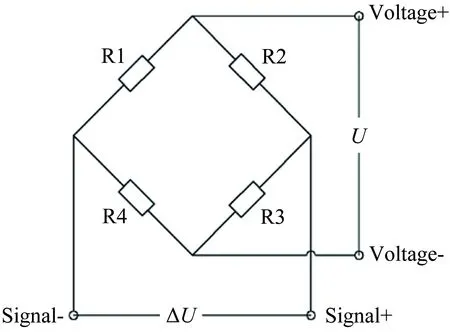
图4 轴向力分量组桥定义

通过天平受载后的应变分布及变形分析进一步对比研究了3种结构形式的轴向力测量元件的干扰特性。基于前述分析，3种结构形式的轴向力元件受纵向载荷(Mz、Y)时的干扰特性存在较大差异，本文以施加法向力(Y)至设计载荷时的干扰为例进行对比分析，施加俯仰力矩(Mz)时的干扰情况与之类似，这里不再赘述。图5所示为施加法向力(Y)设计载荷时3种结构形式的轴向元件应变分布对比，图6和7分别为施加法向力(Y)设计载荷时Config_2和Config_3天平变形及轴向力元件受力分析。

由图5可知，施加法向力(Y)时，Config_1由于轴向力测量元件的纵向刚度较大(纵向刚度甚至大于布置于测量梁两侧的支撑片组刚度)，轴向力元件承受了较大法向载荷，从而使得R1～R4贴片位置处的干扰应变较大。同时，由图5可知， “工”字梁前后表面R1～R4贴片位置处干扰应变值不对称，这会导致电桥有较大的干扰输出，需减弱Config_1轴向力测量梁的纵向刚度(即为Config_2)：通过在测量梁中间沿纵向设置铰链的方式削弱其纵向刚度，从而释放天平受法向载荷时轴向力元件的拉压应力，使得法向载荷和天平变形主要由分布在两侧的支撑片承担，进而减小R1～R4贴片位置处的干扰应变。由图5可知，施加法向力(Y)设计载荷时Config_2的R1～R4贴片位置处的干扰应变显著减小，但干扰应变值仍然不对称，该应变差量无法通过电桥平衡。

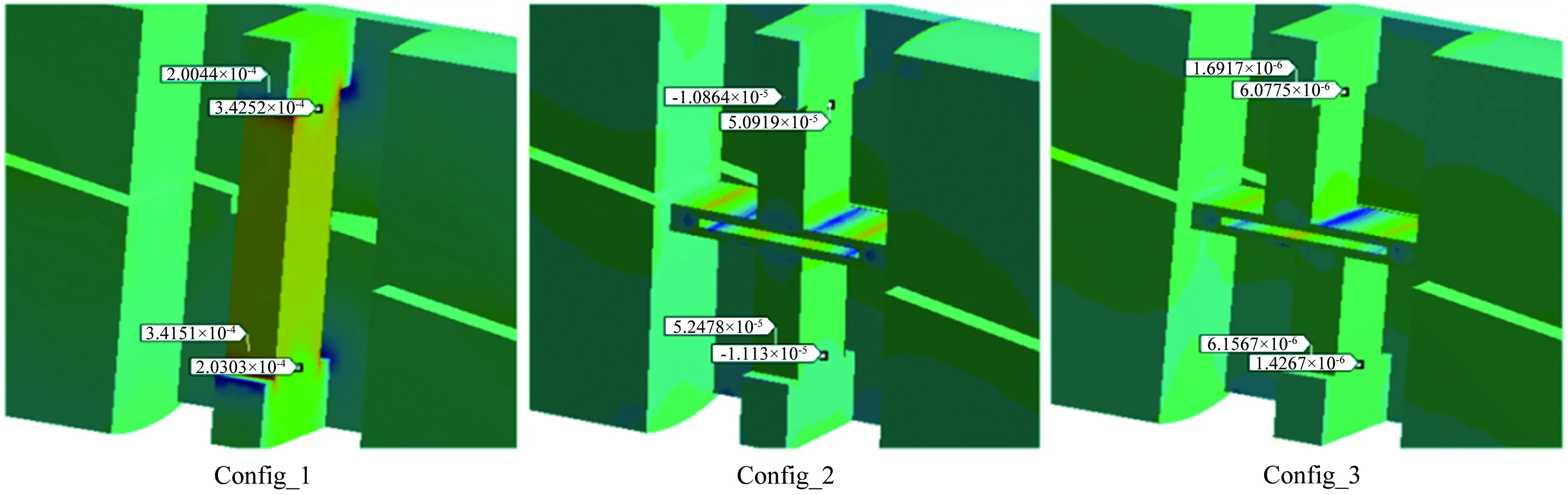
图5 施加法向力(Y)设计载荷时轴向元件应变分布

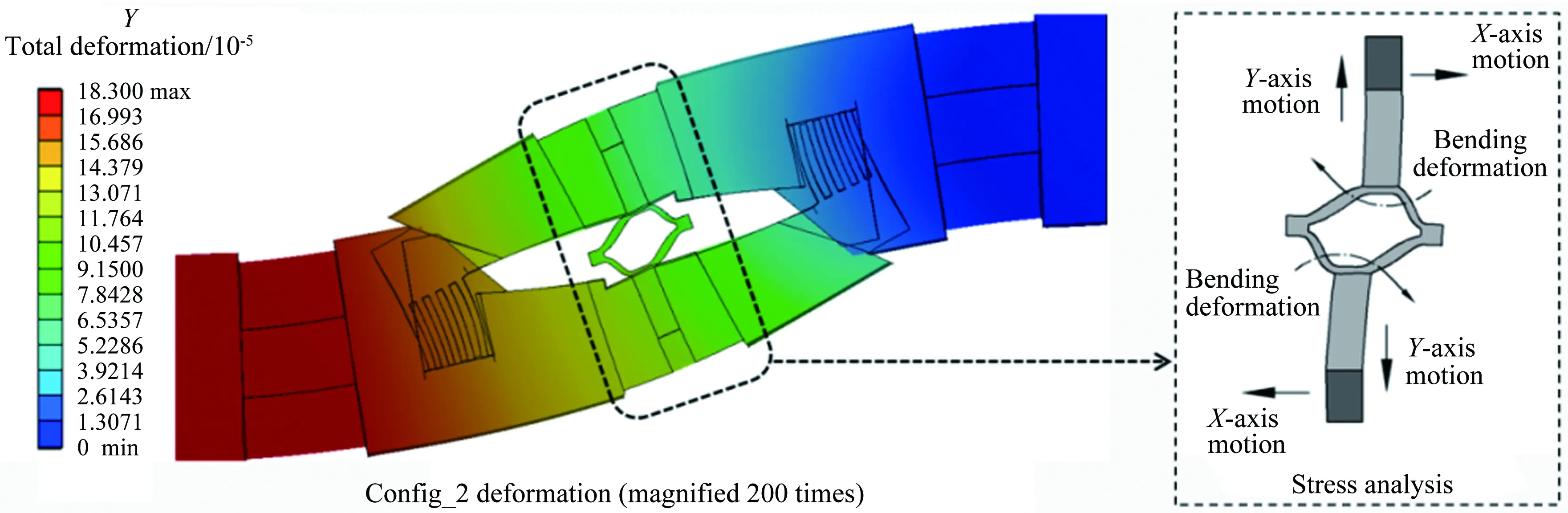
图6 施加法向力(Y)设计载荷时天平变形及轴向元件受力分析，Config_2

图7 施加法向力(Y)设计载荷时天平变形及轴向元件受力分析，Config_3

结合图6分析发现，施加法向力(Y)时，由于天平框体沿轴向的刚度分布不均匀，轴向力测量梁两端连接段既有Y向位移，亦有X向(轴向)位移，而Config_2的铰链沿纵向布置，即只削弱了测量梁沿纵向的刚度，从而释放了天平受法向载荷时轴向力测量梁的Y向位移，亦即释放了大部分拉压应力；而X向位移则会使测量梁产生弯曲应力，2种应力耦合后导致了R1～R4贴片位置的应变输出不对称问题。

通过上述分析，Config_2的R1～R4贴片位置处干扰应变不对称问题主要由天平框体刚度分布不均匀，施加法向力(Y)时测量梁连接段产生X向位移导致的。因此，将上、下测量梁沿天平轴线对称偏移一定对称距离，克服天平框体刚度影响，使其受法向力(Y)时，轴向力测量梁连接段只沿Y向有位移，测量梁不发生弯曲变形，即为Config_3。如图5所示，通过优化设计，Config_3显著解决了R1～R4贴片位置处的应变输出不对称问题，且纵向干扰应变有了进一步的减小。结合图7分析发现，施加法向力(Y)时，轴向力测量元件的铰链框产生对称变形，测量梁两端连接段只沿Y向有位移，而沿X向无位移，从而使得测量梁无弯曲变形。因此，本文采用Config_3作为最终的设计方案，通过有限元方法优化设计，最终上、下测量梁的中线沿天平轴线偏离天平校心各1.2mm，如图8所示。

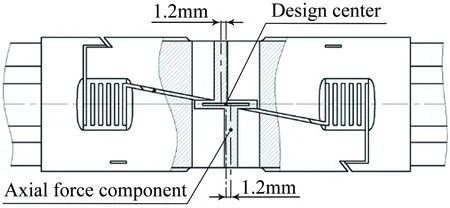
图8 Config_3测量梁偏移尺寸

2 Config_3性能分析

通过上述优化和改进设计，Config_3最终在确保轴向力有足够的灵敏度前提下，各载荷分量对轴向力分量干扰应变近乎为零，彻底解决了轴向力的测量干扰问题。下面就对其灵敏度、干扰特性、模态分析及应力校核等性能作详细介绍。表3所示为单分量施加设计载荷时，各分量主应变和对轴向力的干扰应变输出。由表3可知，本文设计的天平应变输出合理，对各分量测量载荷有足够的分辨率。另外，单分量施加设计载荷时，各载荷分量对轴向力的干扰应变几乎为0，施加纵向载荷(Mz、Y)时，约有4με干扰应变输出，但其只占主应变的2.5%，量值较小，达到了设计目的。

表3 天平各分量主应变及对轴向力的干扰应变(单位：με)Table 3 Main strain output and interference strain on the axial component (unit: με)

图9所示为Config_3与常规“I型”梁结构天平前6阶模态对比。2种结构形式的天平尺寸相同，且分别施加设计载荷时，各分量具有相同的灵敏度，通过比较各阶频率，可定性对比新设计天平与常规天平的刚度。由图9可知，Config_3与常规“I型”梁结构天平的各阶频率相当，表明本文设计在保证有足够灵敏度输出的前提下，天平刚度与常规设计相当，即2种结构形式天平的应变-变形比相当。图10所示为Config_3的有限元强度校核，由图可知，同时对该天平施加六分量设计载荷时，其最大应力σmax约为464MPa左右，危险点在支撑片根部附近。天平材料选用F141，选取冲击因子和安全系数分别为2，则其最大应力小于许用应力[σ]=(1862/4)MPa，满足安全使用要求。

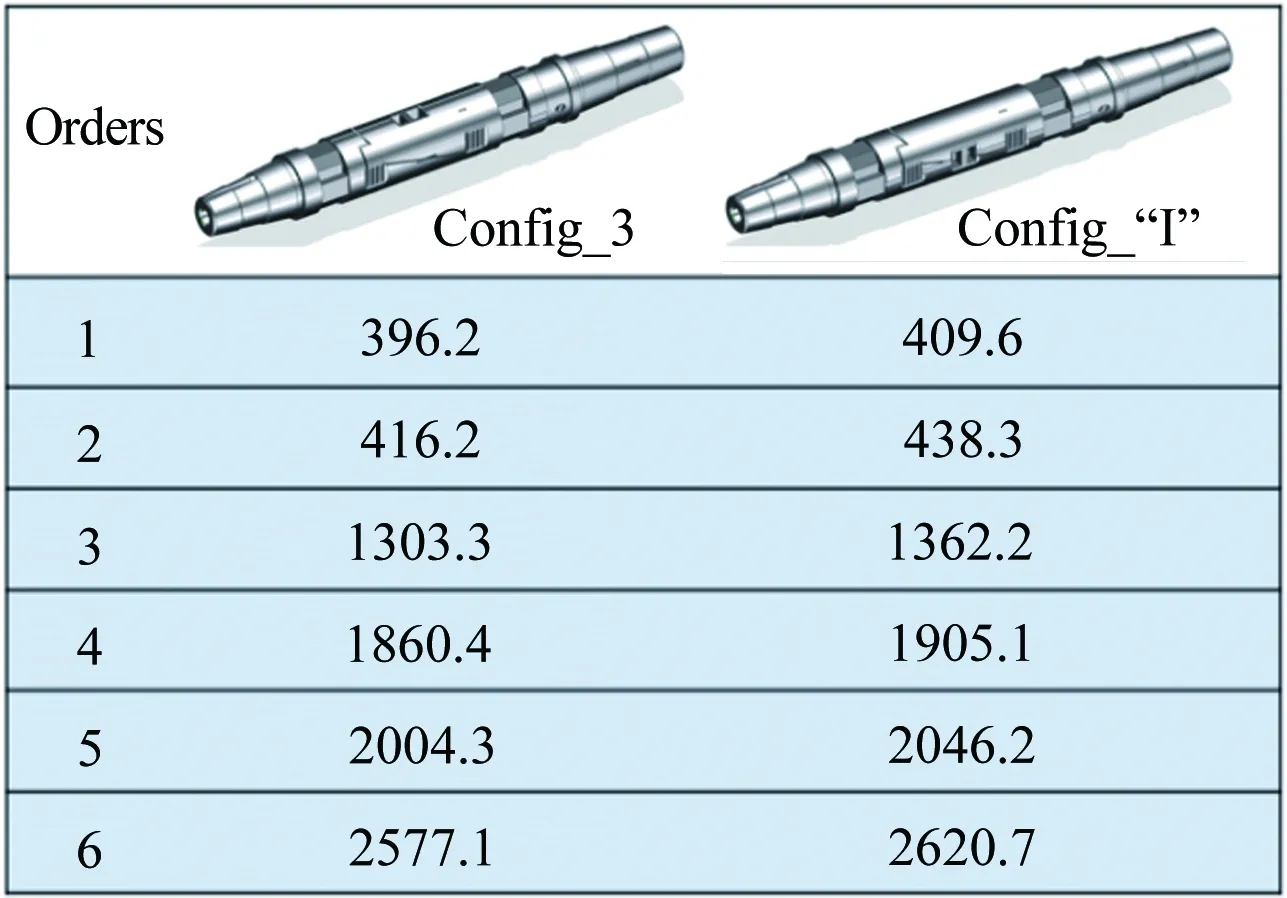
图9 模态对比分析(单位：Hz)

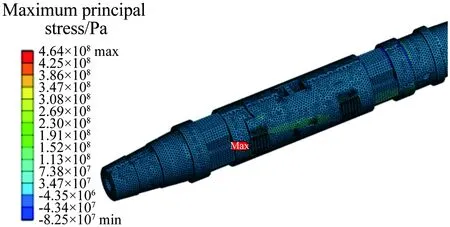
图10 有限元强度校核

3 静态校准

新研制天平在完成机械加工、贴片后，对其进行了静态校准。图11和12分别为贴片完成后的天平实物图和中国航天空气动力技术研究院的ABCS-300型六分量复位式静校系统，天平静校时采用多元加载复位校准的方式。

图11 天平实物图

图12 ABCS-300型静校系统

表4所示为静态校准时单独施加各分量至设计载荷，轴向力(X)的主应变输出和其他分量对轴向力(X)的干扰输出值(单位：μV/V)，以及干扰输出占轴向力主应变输出的百分比。由表4可知，单独施加各分量至设计载荷时，除法向力(Y)和侧向力(Z)对轴向力(X)有干扰输出外，其他分量的干扰几乎为零；而Y和Z分量的干扰值最大只有约0.0075μV/V，只占X分量主应变输出的2%。另外，从该天平的静态校准矩阵可知(如图13所示)，相比于现有常规天平，该天平校准矩阵中各分量对轴向力的一次、二次干扰系数均较小。由此可知，该天平达到了“较小轴向力测量干扰”的设计目的，有效减小了各气动载荷分量对轴向力的测量干扰，降低了轴向力干扰系数的拟合难度和误差，有利于提高轴向力的测量精、准度。

表5给出了静态校准的综合加载误差和综合加载重复性结果，可以看出，新研制天平各分量具有良好的测量重复性和较小的测量误差，尤其是轴向力分量，其综合加载误差和综合加载重复性精度达到了国军标GJB2244A-2011[11]中的先进指标要求。

表4 轴向力(X)主输出、干扰输出及占比Table 4 Main strain output and the interference output of X

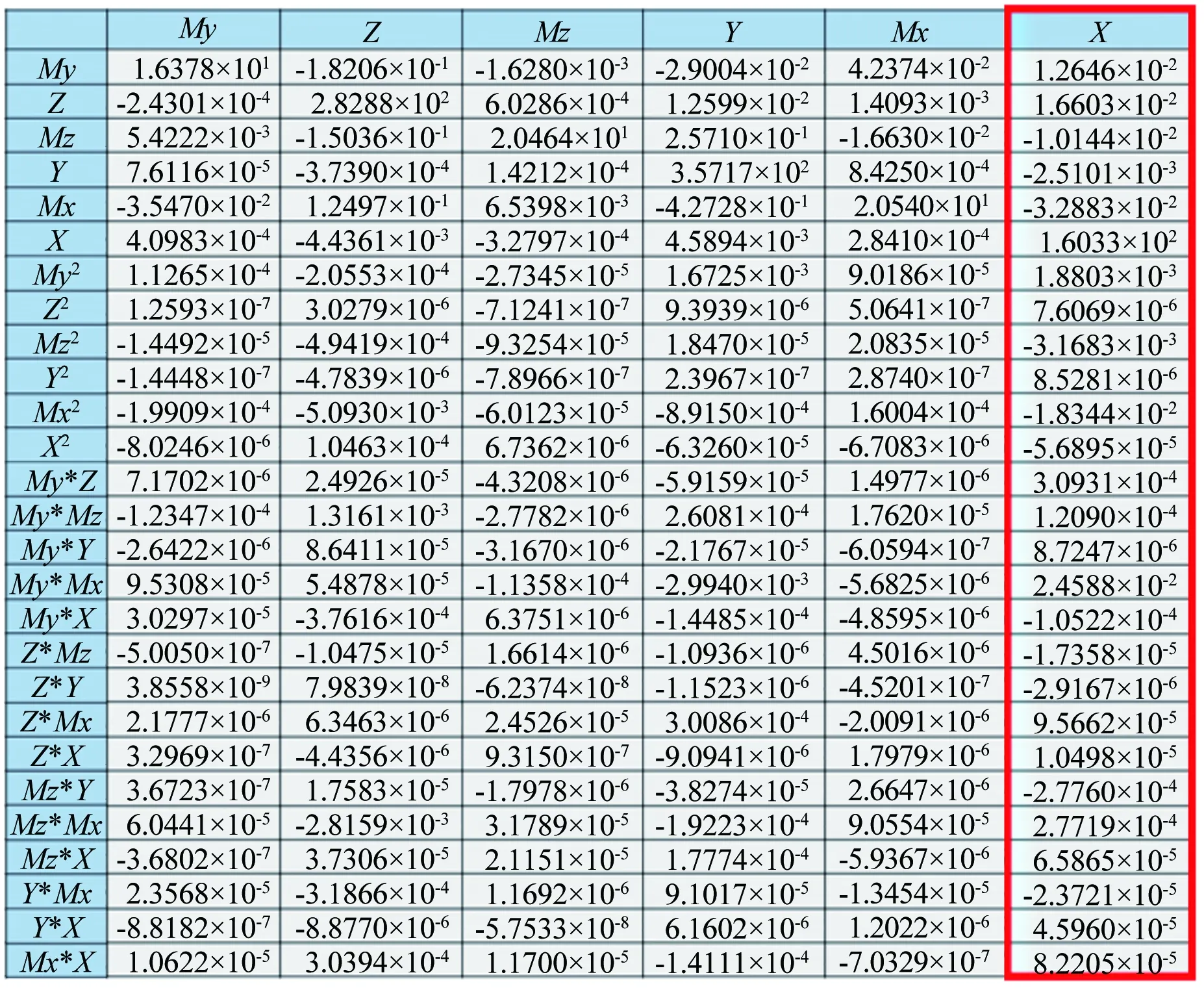
图13 天平校准公式

MyZMzYMxX综合加载误差/%FS0.080.080.060.020.130.14综合加载重复性/%FS0.030.020.010.010.050.08

4 标模试验

静态校准完成后，需通过标模试验对天平性能进一步检验。标模试验在中国航天空气动力技术研究院的FD-12风洞进行(见图14)。FD-12风洞是一座暂冲式亚、跨、超三声速风洞，可满足马赫数0.4～4.0的风洞试验需求，是目前CAAA的主力风洞之一。

图14 中国航天空气动力技术研究院FD-12风洞

表6所示为ADA-028324(8#)标模在Ma=2.0时的重复性精度试验结果以及箭弹测力模型精度指标[12](1.5≤Ma≤4.0)要求，由表6可知，新研制天平的标模试验结果良好，重复性精度满足指标要求。

表6 8#标模在Ma=2.0时的重复性精度Table 6 The repeatability precision of the 8# standard model,Ma=2.0

5 结 论

针对目前风洞测力试验技术的发展对风洞天平测量精度的更高需求，研制了一台较小轴向力测量干扰的六分量杆式应变天平，并实施了静态校准和标模试验，检验了新研制天平的轴向力干扰特性及测量精、准度等性能。

(1) 轴向力结构设计采用将测量元件置于天平轴线上“设计中心位置”的方式，通过在测量梁上设置铰链以及轴向测量梁的非对称设计，最终使各气动载荷分量对轴向力的干扰应变输出近乎为零，而无需通过电桥去消除，彻底解决了轴向力的测量干扰问题。

(2) 有限元结果表明，在保证灵敏度输出以及天平强度和刚度不减的前提下，优化改进后的Config_3可视为较为理想的设计结果；设计还改善了天平各分量载荷作用在轴向力测量梁上交错复杂的应力分布状态，提高了天平轴向力的长期稳定性。

(3) 静态校准结果表明，新研制天平各分量对轴向力的测量干扰均在2%以内，降低了轴向力干扰系数的拟合难度和误差，同时，各分量具有良好的静校重复性和较小的测量误差，轴向力分量综合加载误差和综合加载重复性甚至达到了国军标先进指标要求。

(4) 标模试验结果表明，新研制天平标模试验结果良好，试验重复性精度满足箭弹测力模型精度指标要求。结合静态校准和标模试验结果，该天平轴向分量具有较高的测量精、准度，可满足现代风洞试验高精度轴向力测量的需求。