粗糙元对高超声速边界层转捩影响的研究进展

董 昊, 刘是成, 程克明

(南京航空航天大学 航空宇航学院, 南京 210016)

0 引 言

一直以来，边界层转捩就是湍流研究领域的热点问题，由于其复杂性、现有方法的局限性以及风洞试验存在较大难度，对边界层转捩很多问题的认识或不清楚，或有争论，甚至还存在许多未知的问题[1]。近年来，随着高超声速飞行器的发展，边界层转捩问题更加突出。高超声速飞行器复杂外形产生的复杂流动会导致特殊的边界层转捩现象，形成多种转捩机制并存、湍流区与层流区不断变化的复杂形式[2]。在实际工程中，边界层转捩对高超声速飞行器气动设计具有重要影响。具体来说，边界层转捩将影响飞行器气动加热、表面摩擦阻力、进气道流量、发动机燃烧效率和工作效率等一系列问题。对于高超声速飞行器，粗糙元诱导转捩是重要的转捩形式之一。通过研究粗糙元不同参数对高超声速边界层转捩的影响，探求粗糙元诱发转捩的物理机理以及针对工程应用的相关预测准则，具有重要的研究意义。

粗糙元对边界层转捩影响的研究从20世纪50年代就已开始，并取得了一系列研究成果，尤其是Schneider等[3-4]开展了大量研究工作，并在其综述文章中[3]强调了研究的3个主要方向：粗糙元促成转捩的机理、粗糙元引起转捩的最小尺寸、粗糙元不能引起转捩以及不影响转捩位置的最大尺寸；总结了粗糙元影响转捩的3种模式：(1)粗糙元会在尾迹区产生流向涡结构和不稳定剪切层。当粗糙元尺寸大于其“有效高度”时，粗糙元下游将立即发生转捩，但当其尺寸较小时，转捩可能会在距离粗糙元较远的下游位置发生，其原因可能是剪切层失稳或尾迹涡失稳诱导所致。(2)当粗糙元尺寸较小时(基于粗糙元高度的雷诺数Rek<10)，横流、Görtler涡以及瞬态增长机制是导致粗糙元后流向涡增长并最终失稳的原因。(3)来流扰动也是影响粗糙元后流动失稳的原因，如声波与粗糙元相互作用会产生第一、第二模态的扰动波等。上述结论均是在风洞试验和飞行试验数据分析中得到的验证性结果，缺乏理论的强力支撑。

除Schneider外，Reda[5]、Iyer[6]、罗纪生[7]、陈坚强[8]等在其综述文章中均对与粗糙元相关的高超声速边界层转捩进行了部分概述。前述文献主要是针对粗糙元类型(孤立、离散/分布)和自身参数(高度、形状、间距等)、转捩控制效果(促进、推迟)等进行综述。本文侧重已有综述文献未涉及或未详细介绍的内容，回顾近年来不同类型粗糙元对高超声速边界层转捩影响及控制的最新研究进展，阐述粗糙元在高超声速转捩机理相关研究中的作用，简要介绍在南京航空航天大学高超声速风洞(NHW)中开展的部分研究工作，总结展望粗糙元对高超声速边界层转捩影响研究的发展趋势。

1 粗糙元对转捩影响的最新研究进展

粗糙元对层流及转捩的控制，不仅是空气动力学研究的前沿热点问题之一，其在高超声速飞行器气动力和气动热设计中也占有重要地位，具有重大的工程应用价值。一方面，高超声速飞行器表面防热瓦之间有一些填充物，当这些填充物受热发生变形，形成飞行器表面的凸起和凹陷，这种大的粗糙元或者小的粗糙度可以诱发边界层转捩。根据美国国家航天飞机(NASP)项目的经验，由于湍流的热传导率比层流大很多，飞行器在全层流状态下的有效载荷与总重量的比值是全湍流状态下的两倍左右[9]，因此，必须采取一定措施来抑制层流向湍流的转变。另一方面，在高超声速吸气式飞行器设计中，保证进气道入口处的湍流状态可以为推进系统提供足够的进气流量，并可促进燃烧室中空气和燃料的混合。因此，通常在飞行器前体或进气道入口前一定距离处放置粗糙元或粗糙带，人工促使流动从层流转变为湍流。在美国X-33、X-43和X-51等高超飞行器验证计划中，都对该类转捩形式给予了极高重视[10-13]。

1.1 高超粗糙元的分类

开展粗糙元对高超声速转捩控制研究的首要工作是对高超粗糙元进行合理分类。通常情况下，从几何形状上，高超粗糙元可以分为规则(regular)和不规则(irregular)两类；从分布形式上，高超粗糙元亦可分为孤立(isolated)和离散/分布(discrete/distri-buted)两类。本文将以上两种分类方式结合，对高超粗糙元进行分类，如图1所示。

图1 高超粗糙元分类

按分布形式，规则粗糙元可分为孤立、离散两类。孤立粗糙元又可分为二维和三维粗糙元。当粗糙元某个方向的尺度远大于另外两个方向，可视为二维粗糙元。常见的二维粗糙元有展向台阶、凹腔等。三维粗糙元则通常表示粗糙元尺度在三个方向上大小相似，比如圆柱、方形、菱形等规则的凸起或者凹腔。当许多孤立的规则粗糙元以某一特定规律集中分布于一块区域，可以称之为离散式粗糙元，如不同形状、间距、高度/深度的粗糙元凸起/多孔壁面，此时的流动通常会受到各粗糙元分布参数的影响。同样，不规则粗糙元也可分为孤立和分布的不规则粗糙元(度)。在实际飞行中，高超声速飞行器往往会遭遇物理损伤或高温烧蚀，在其热防护系统(Thermal Protection System，TPS)上形成形状不规则的凸起或凹陷。一般情况下，物理损伤多为单一形式，即孤立不规则粗糙元；表面由于气动加热烧蚀或融化形成的凹凸不平，如砂砾结构、蜂窝结构等，则属于典型的分布式粗糙度。

下文将开展规则和不规则粗糙元对高超声速转捩影响相关研究的综述：主要叙述规则高超粗糙元研究中较为集中的表面凸起粗糙元，简要介绍凹腔和多孔壁面对高超声速转捩影响的研究进展；不规则高超粗糙元方面，则主要总结说明分布式粗糙度对高超声速转捩影响的研究进展。

1.2 规则粗糙元对高超声速边界层转捩影响研究

1.2.1表面凸起粗糙元

形状规则的表面凸起粗糙元是最为常见的高超声速边界层强制转捩装置[14]，研究者已开展了大量研究工作[15-19]。影响此类粗糙元对转捩控制效果的因素很多，如粗糙元的几何参数(高度、宽度、形状、相邻粗糙元的间距)、当地边界层厚度、来流雷诺数与马赫数[20]、迎角、壁温、自由流湍流度[21]等。对于孤立表面凸起粗糙元，大多数对其控制转捩机理及效果的研究主要集中于几何参数；而在众多几何因素中，粗糙元的高度[22-23]对转捩效果起着最为重要的作用。

图2显示了典型的球状粗糙元的高度对可压缩边界层转捩的影响[22]，对应的马赫数范围为1.97～3.84。从图中可以看出，当粗糙元高度高于“有效高度”时，粗糙元会对边界层转捩位置造成一定影响；而当粗糙元高度达到所谓“临界高度”时，转捩会在粗糙元处立即发生。

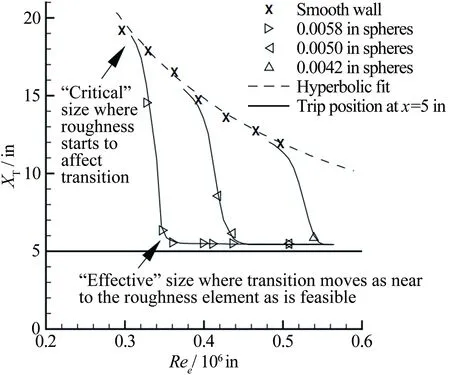
图2 粗糙元临界高度和有效高度[22]

Wheaton等[23]在普渡大学Boeing/AFOSR Mach 6静风洞中系统研究了圆柱形粗糙元不同高度(0.2～1.2倍当地边界层高度)对转捩的影响及相应的物理机理。研究发现，粗糙元高度较低时，其后方尾流中的扰动主导频率为40～70kHz；当粗糙元高度增加至对应的雷诺数Rek大于6×104时，扰动主导频率变为20～25kHz。这说明粗糙元高度的变化必然会引起感受性、失稳机理的改变，但其根本原因和影响规律还不得而知。

另外，孤立表面凸起粗糙元的形状也是影响转捩控制效果的主要因素。斜坡、钻石、正方形、半球形和圆柱体是典型的粗糙元形状，不同形状的粗糙元诱导转捩机理和效果并不相同。Zhou等[24]系统研究了不同马赫数下(Ma=3.37～6.63)不同粗糙元形状对转捩的控制效果，发现方形、钻石形粗糙元诱导转捩效果明显优于圆柱形和半球形；并且，随着马赫数的提高，粗糙元诱导的转捩位置延后，表明压缩性对粗糙元的诱导转捩效果有很大影响。朱德华等[25]利用DNS研究了Ma=6来流条件下斜坡形、对齿形粗糙元诱导转捩的特性以及工程应用。研究表明，相较于斜坡形粗糙元，对齿形粗糙元具有多种涡结构失稳模式，因而具有更强的诱导转捩能力和更低的有效高度，其能够有效诱导转捩对应的飞行范围更为广泛。

与孤立粗糙元相比，离散式表面凸起粗糙元对高超声速边界层转捩的影响更为复杂[3]。离散式粗糙元引起的扰动源远多于孤立粗糙元，因此很难区分不同扰动源在诱导转捩过程中的主导作用。尽管在离散式粗糙元对高超声速边界层转捩控制效果的研究中发现，相邻粗糙元的间距往往是关键影响参数，但其原因至今尚无明确解释。Whitehead等[26]系统探讨了圆柱形离散式粗糙元间距对高超声速边界层转捩的影响，发现当s/w>3(s为粗糙元间距，w为粗糙元宽度)时，粗糙元间距对转捩过程没有影响；当s/w<3，孤立粗糙元周围的流场会受到相邻粗糙元的强烈影响而加快转捩的发生；但当相邻粗糙元十分接近时，转捩的促进效果反而又降低了。最近，Duan和Xiao[27]利用DNS研究了来流马赫数6时、相邻斜坡形粗糙元间距对高超声速边界层转捩的影响。结果表明，随着相邻粗糙元间距的减小，尾迹涡之间存在相互干扰，从而导致转捩提前发生。

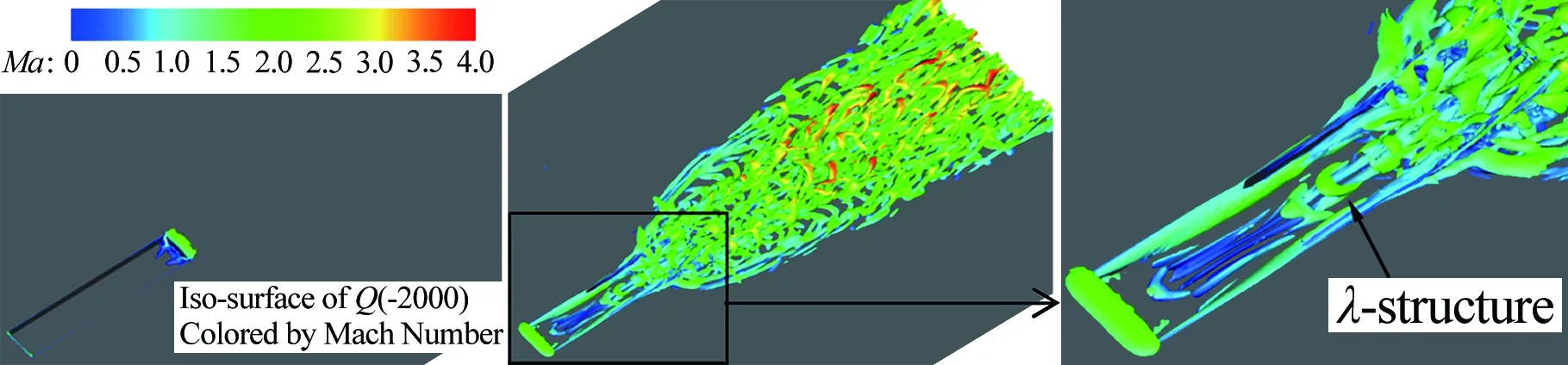
近年来，随着大规模计算条件和先进实验测量技术的应用和发展，研究者发现了更多的粗糙元对高超声速边界层转捩控制的细节。在数值模拟方面，Duan[28]等利用DNS研究了孤立圆柱形粗糙元诱导的高超声速边界层转捩。数值模拟结果表明，马蹄涡和粗糙元后剪切层的不稳定性是影响边界层转捩的主要因素。Subbareddy[29]等采用动力学模态分解(DMD)方法，对粗糙元产生的马蹄涡和分离剪切层的演化进行了较为深入的研究。研究结果显示，频率为20、40和53kHz的3种扰动模态，分别代表非定常马蹄涡及其谐波模态以及上卷的剪切层模态，如图3所示。

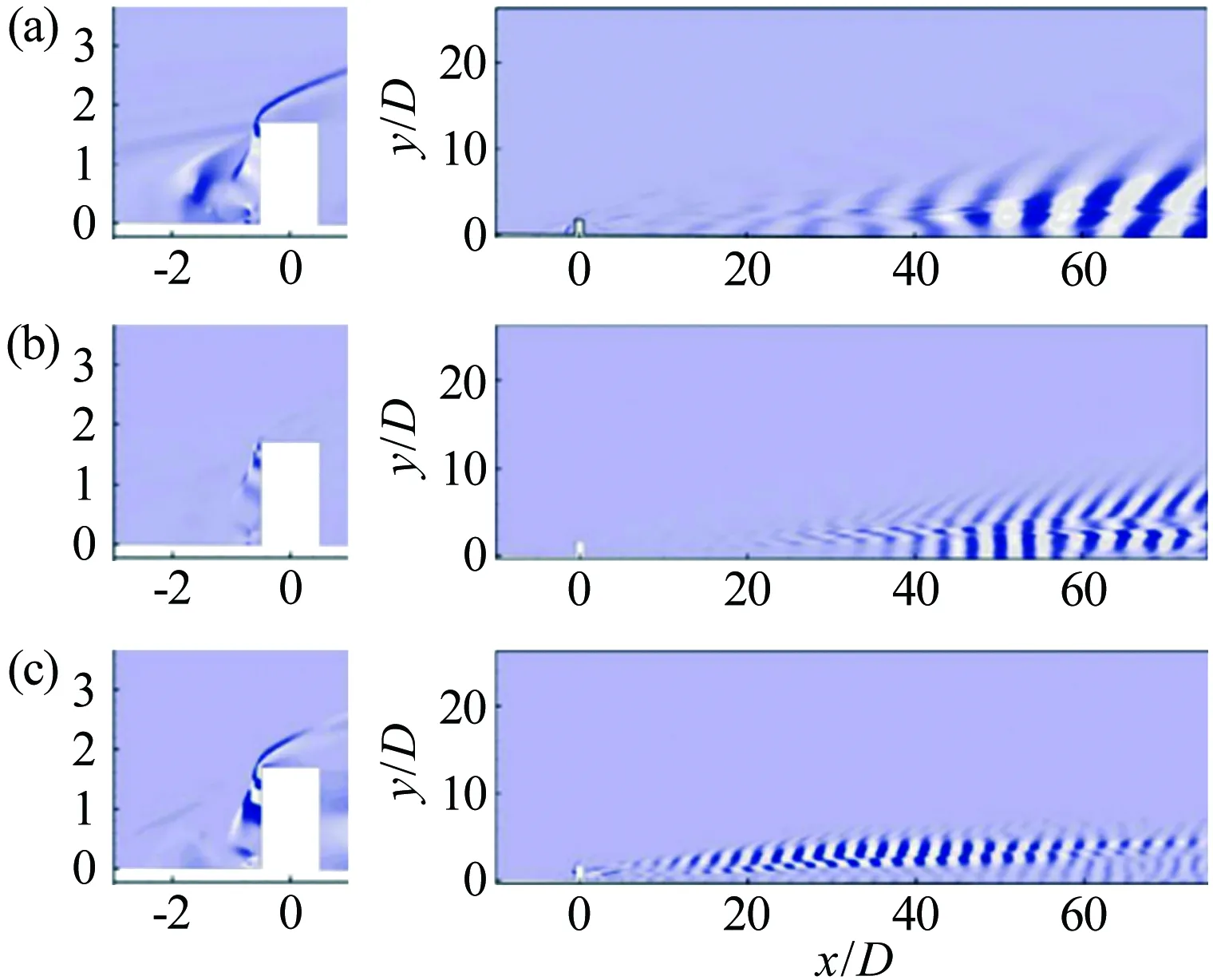
图3 基于DMD的粗糙元尾迹模态显示((a), (b), (c)分别表示20、40和53kHz的3种扰动模态)[29]

Fig.3VisualizationofdifferentmodesinthewakeofroughnesselementsbasedontheDMDmethod(a,b,crespectivelydenotethreedisturbancemodesof20,40and53kHz)[29]

在风洞实验方面，Danehy等[30]利用一氧化氮平面激光诱导荧光(NO-PLIF)方法研究了来流马赫数为10、带有半径2mm半球的平板上的高超声速边界层流动，由NO-PLIF图像确定的边界层厚度与数值模拟结果一致。在普渡大学Mach 6静风洞中，Wheaton等[31]首次对粗糙元引起的高超声速层流边界层的不稳定性进行了全面的实验研究。Wheaton利用皮托探针、热线探针和壁面高频压力传感器对粗糙元尾迹中的脉动信号进行了检测。结果表明，沿着粗糙元尾迹，不稳定性的振幅逐渐增大，无量纲化的质量流量脉动值接近35%。另外，随着粗糙元高度的减小，这种不稳定性逐渐减弱并最终消失。Ye等[32]利用三维层析粒子图像测速技术(Tomo-PIV)，研究了Ma=6.5流场下、微型斜坡粗糙元下游的高超声速边界层的转捩特征，发现最大速度波动集中于靠近斜坡粗糙元中心处的低速区域，即流向涡附近。在北京大学Mach 6静风洞中，Tang等[33]利用多种测量手段研究了带二维粗糙元的平板边界层的稳定性，并且利用近壁粒子图像测速技术(Near-wall PIV)首次拍摄到了第二模态不稳定波经过粗糙元的瞬时速度场和流动结构。结果表明，二维粗糙元能够成功抑制第二模态不稳定波的发展，如图4所示。在中国空气动力研究与发展中心的Ф500mm高超声速风洞中，Zhao等[34]利用基于纳米粒子的平面激光散射技术(NPLS)，在来流马赫数5时对9个分布式斜坡形粗糙元诱导的平板边界层转捩进行了实验研究，并与隐式大涡模拟(ILES)的结果进行了对比。研究发现，风洞中粗糙元诱导的转捩位置比相同状态下数值模拟的靠前许多，该项研究将原因归结于风洞来流噪声或数值模拟中的耗散。

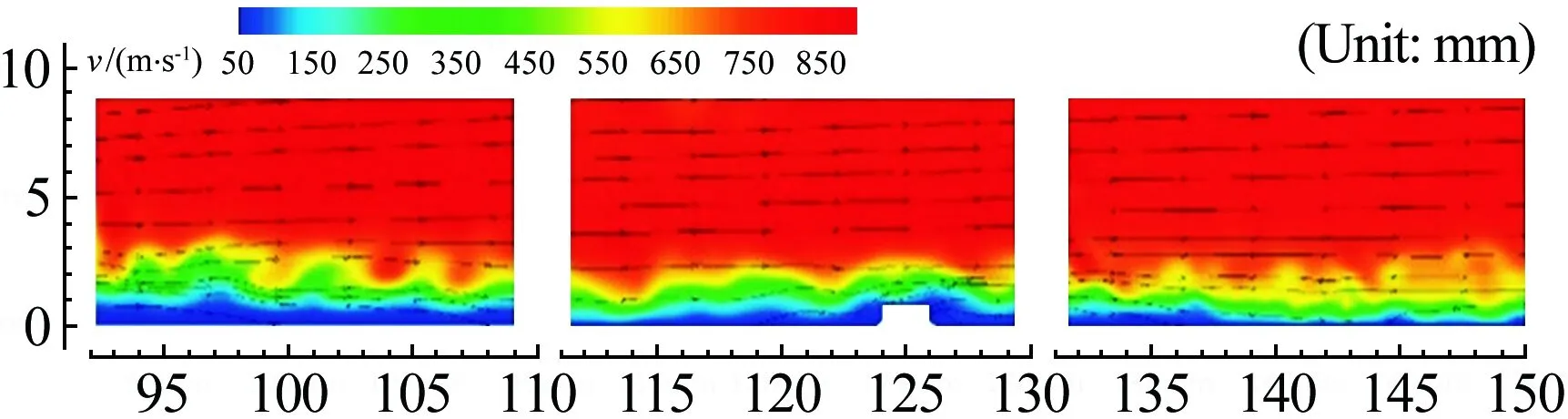
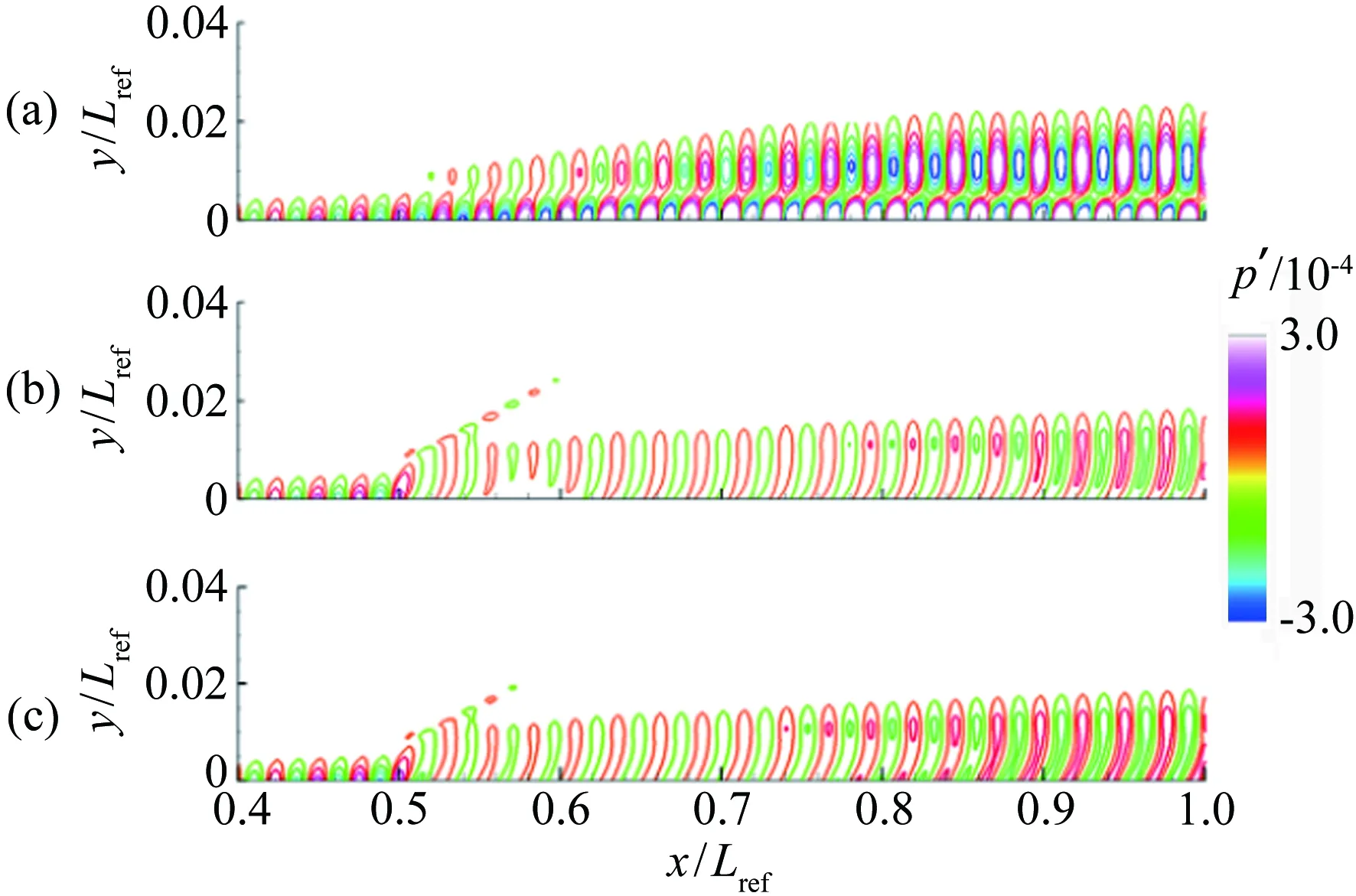
图4 粗糙元上下游瞬时PIV流场图[33]

Fig.4InstantaneousPIVflowfieldofupstreamanddownstreamofroughnesselement[33]

1.2.2表面凹腔

早期研究表明，在高超声速边界层流动中，表面上的缝隙或凹腔会引起下游区域过早地从层流转捩到湍流，导致表面摩擦阻力和热流密度快速增加，进而影响高超声速飞行器的气动力和气动热性能[35]。针对凹腔流动，前人已经进行了大量数值模拟和风洞实验研究。

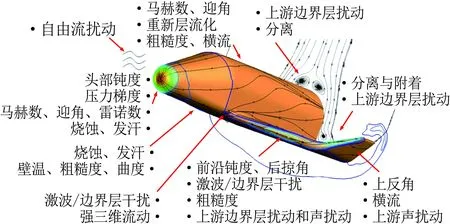
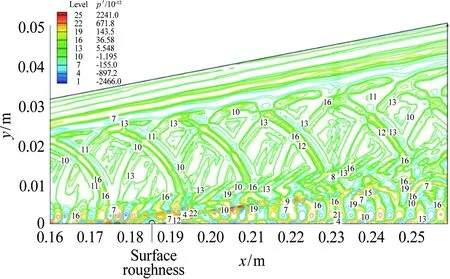
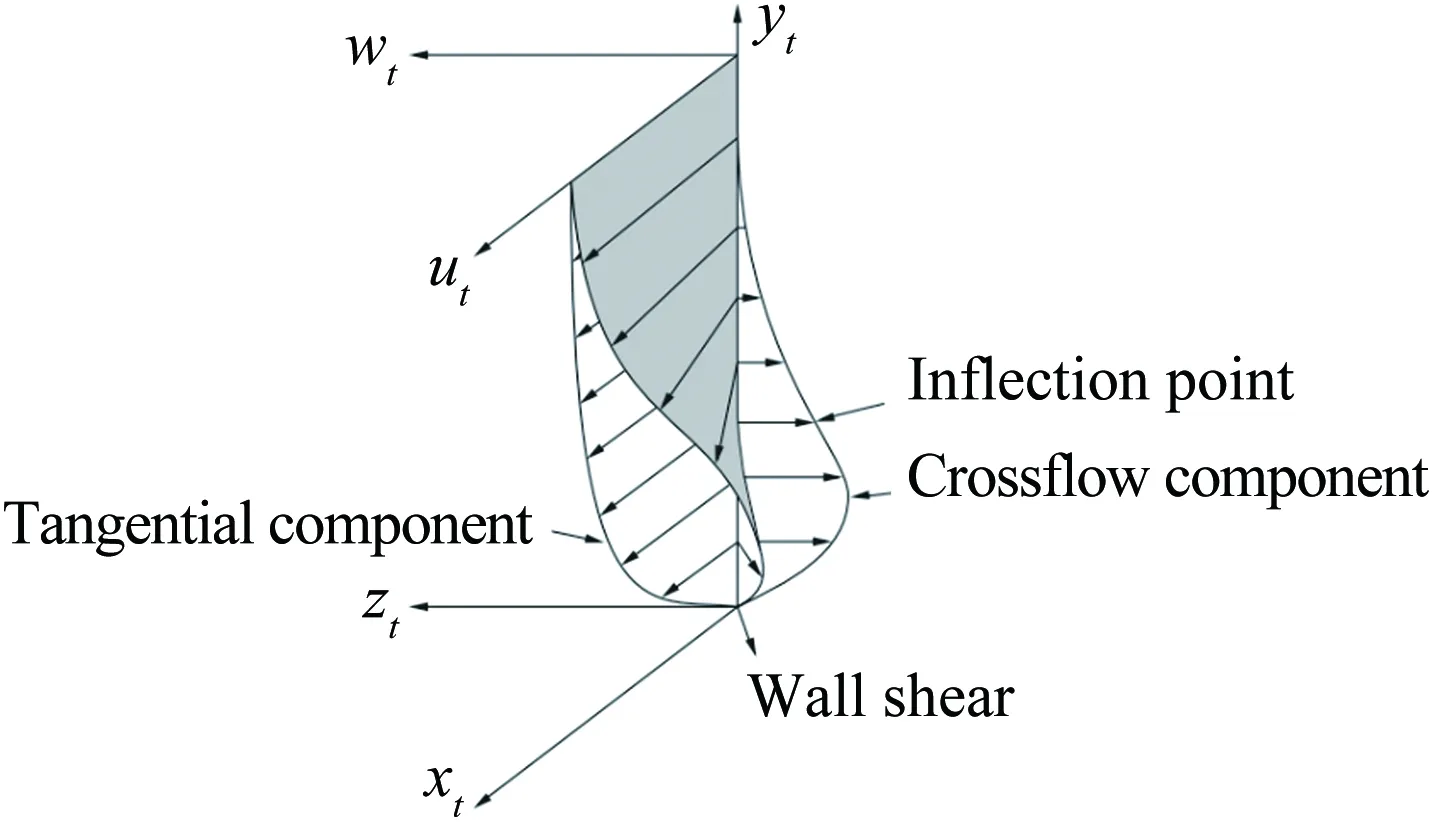
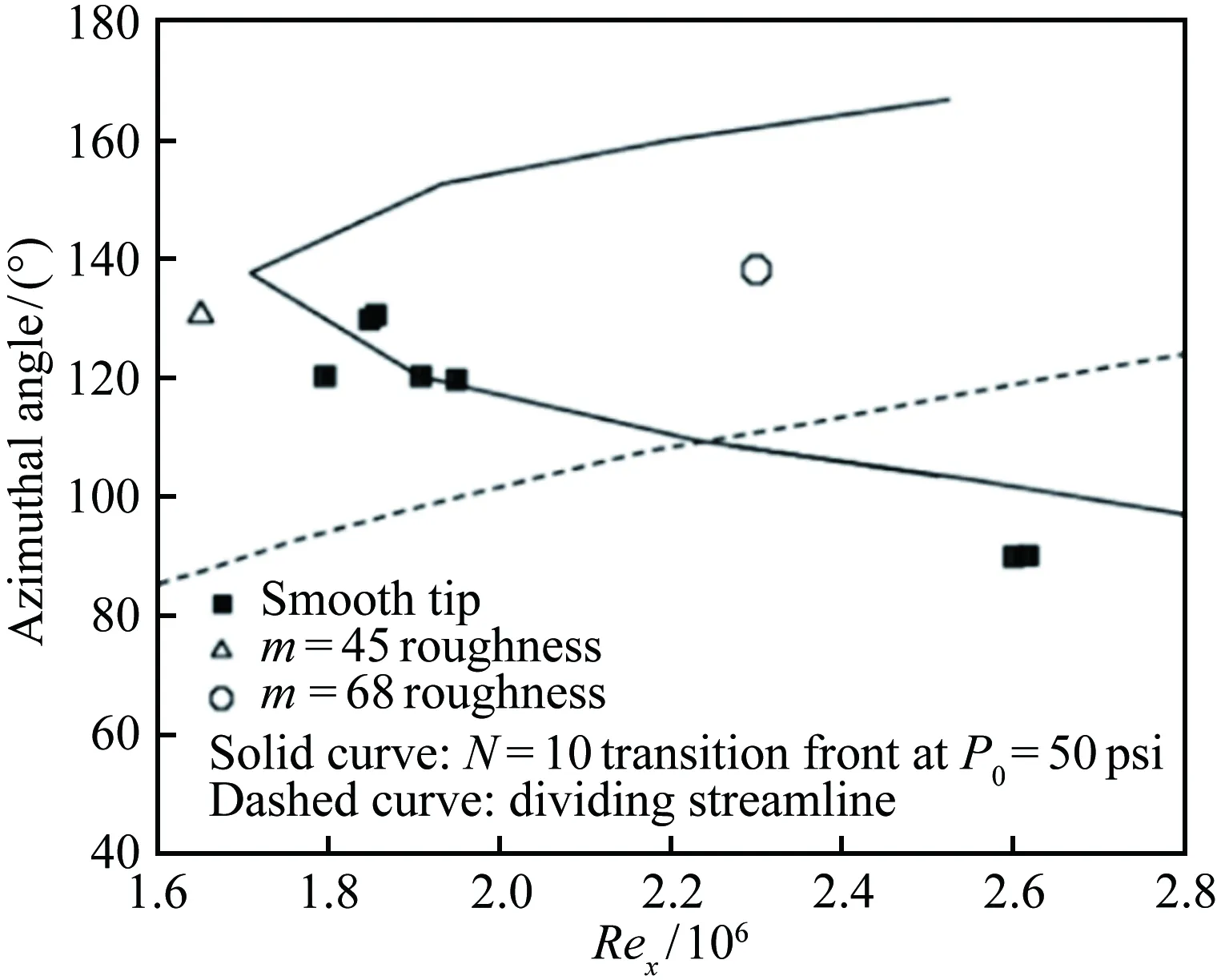
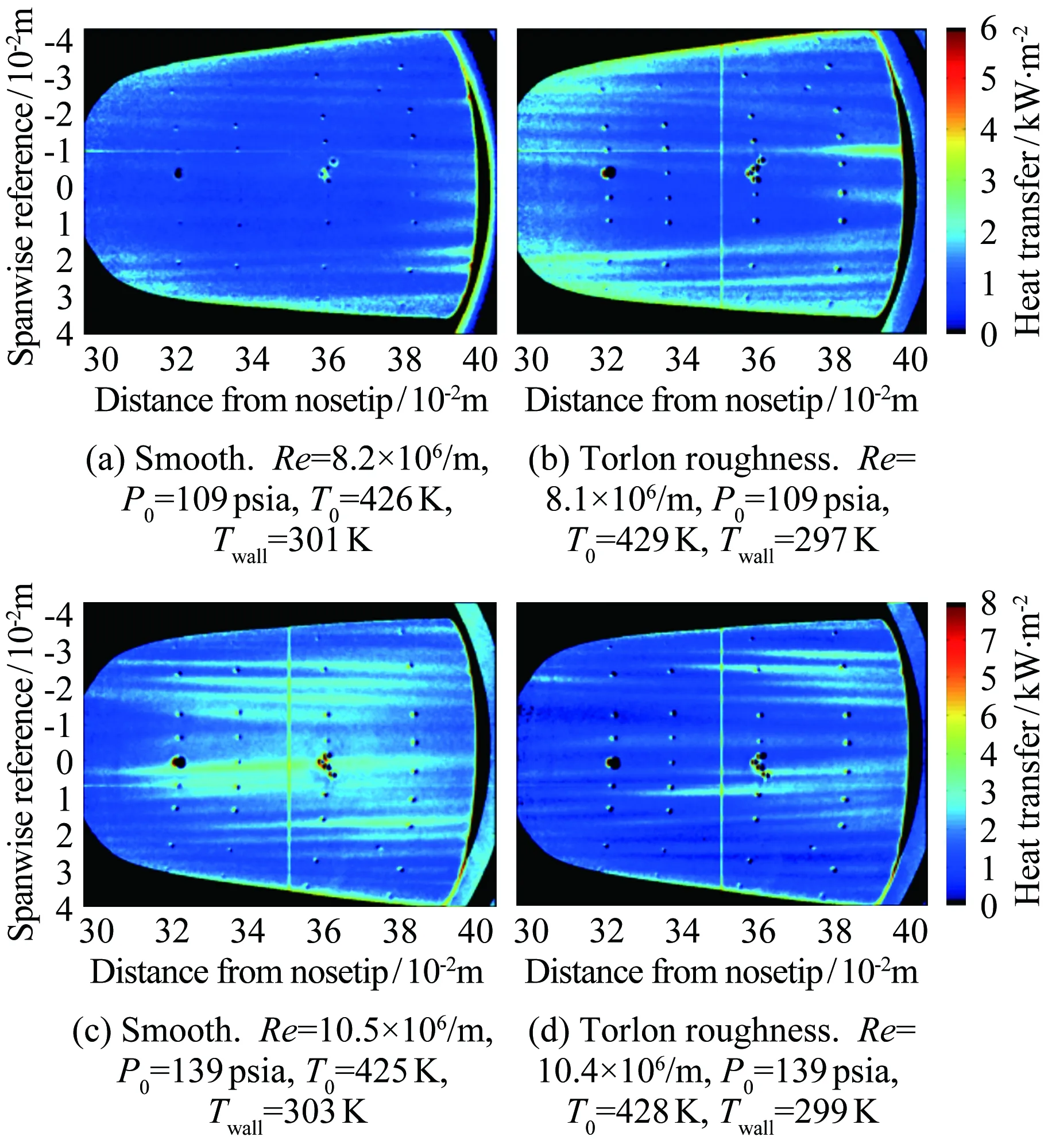
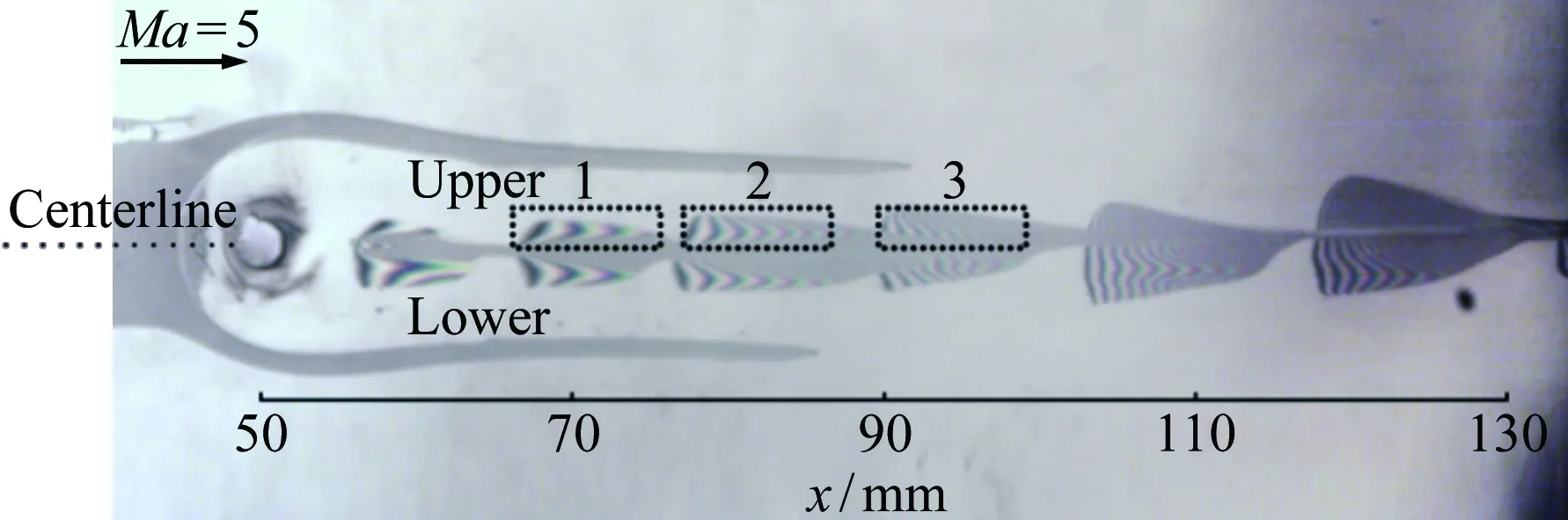
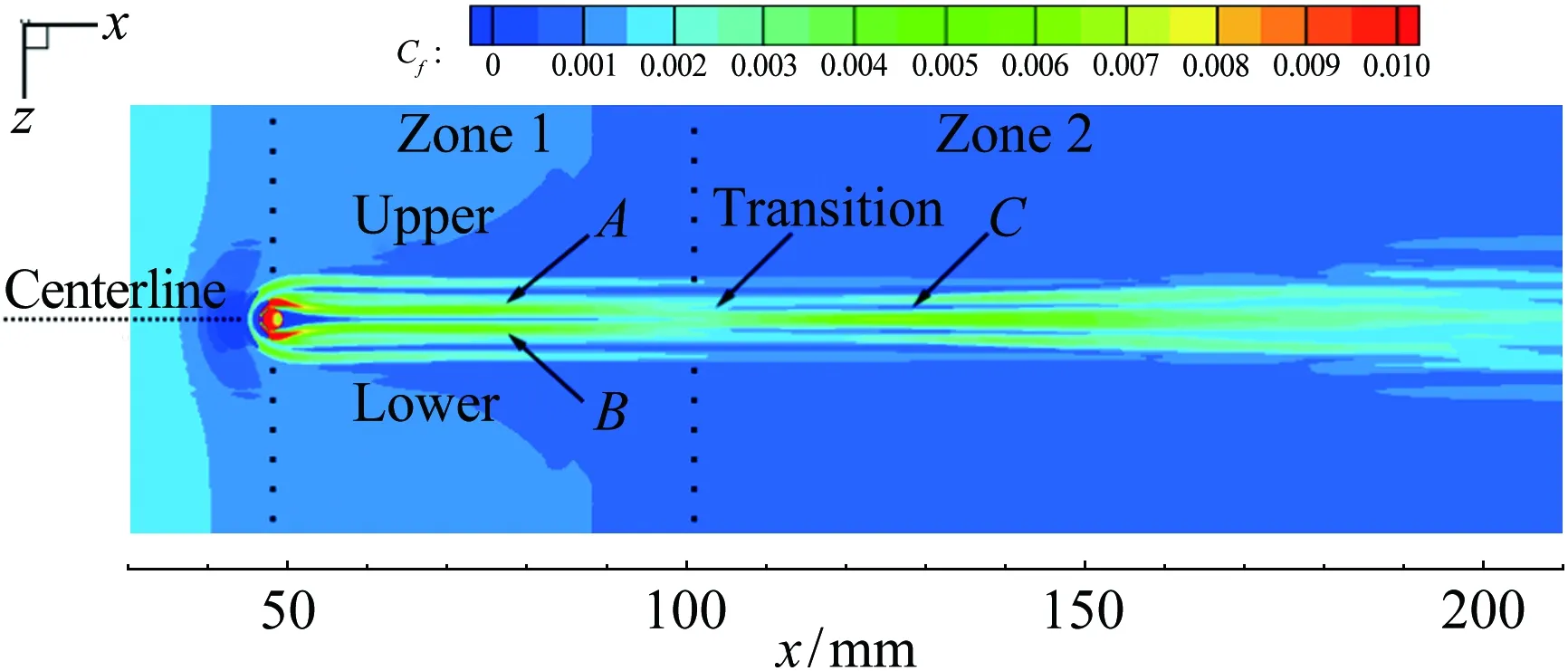
Lawson和Barakos[36]详细综述了高超声速下凹腔对转捩的影响，认为凹腔可导致发夹涡的自发脱落和尾流的不稳定，且凹腔诱导转捩的促进作用与凹腔几何结构密切相关。对于二维凹腔，往往以长深比(L/D)的大小来定义“开腔”“过渡腔”和“闭腔”三种流动状态。当L/D<10，此时的流动称为“开腔”流动，在“开腔”流动中，回流会填满整个腔体；当L/D>14，则称为“闭腔”流动，此时凹腔内的回流区不能延伸到整个凹腔，就像是后台阶流动和前台阶流动的组合；当10

近年来，高超声速凹腔流动对边界层转捩影响的研究逐渐增多。Ohmichi和Suzuki[38]利用数值模拟和风洞实验研究了Ma=7条件下带三维矩形凹腔的平板流动。研究发现，凹腔在其内部和外部诱导了流向的涡结构，这些涡增强了凹腔内壁及下游区域的加热速率，促进了层流到湍流的转捩过程。Chang等[39]利用DNS研究了圆柱形凹腔对高超声速(Ma=6)边界层转捩的影响。研究发现，当雷诺数逐渐升高，圆柱形凹腔尾流中存在发夹涡结构脱落现象，且造成了下游壁面温度升高、剪切层失稳，如图5所示。

图5 圆柱凹腔引起的发卡涡结构[39]

为研究三维凹腔诱导转捩机理，Xiao等[40]采用改进延迟脱体涡模拟(IDDES)方法对三维矩形腔体高超声速流动(Ma=9.6)进行了研究。研究发现，凹腔在-10°迎角时处于“开腔”状态，在-15°迎角时为“闭腔”状态。对于“开腔”状态，剪切层基本稳定，流动保持层流；对于“闭腔”状态，外流进入凹腔并撞击其底部，反射激波和出口激波的存在最终导致流向涡破裂，触发流动很快转捩，如图6所示。

图6 长方形凹腔引起的流向涡结构(左：-10°，右：-15°)[40]

1.2.3多孔壁面

高超声速边界层转捩控制手段很多，其中很有前景的一项技术是由Fedorov等[41]提出的壁面多孔涂层技术。多孔涂层对主流影响很小，并且能够有效抑制高超声速边界层内最不稳定的第二模态的发展，延迟转捩的发生[42-44]，以上结论已被一些实验所证实[45-47]。

Wartemann等[48]用数值模拟方法研究了多孔涂层壁面的孔形状和孔径对稳定性的影响，结果表明，随着孔径增加，产生了额外的阻尼效应。近期，Lukashevich等[49]研究了第二模态对多孔涂层放置位置的敏感性。研究表明，如果涂层在第二模态扰动的不稳定区域内，则对第二模态起到稳定作用，如果涂层在稳定区域内，则会使第二模态不稳定，从而定性地证实了Wang和Zhong[50]之前的数值计算结果。Zhao等[51]建立了一个理论模型来描述平面超声波在多孔涂层上的声学特性，该模型考虑了高阶衍射模式以及相邻腔体之间的相互耦合，成功预测了一个与数值结果相符的反射频率，并使通过该模型优化的腔体几何参数具有最小的反射系数。结果表明，在Ma=6的平板流场中采用优化后的多孔涂层，Mack第二模态被强烈抑制，最大脉动压力降低约88%，如图7所示。

图7 模型表面瞬时压力脉动场分布((a) 没有涂层，(b) 优化后的涂层，(c) 传统涂层)[51]

Fig.7Instantaneousfluctuatingpressurefieldsfor(a)baselinecasewithoutporouscoating, (b)optimizedone,and(c)conventionalone[51]

由此可见，针对规则粗糙元对高超声速边界层转捩的影响，已经形成了较为丰富的理论模型。一方面，不同的规则粗糙元参数(形状、高度、间距等)对促进转捩具有不同的影响规律；另一方面，通过设置合适的规则粗糙元参数(高度、间距等)，在下游激发特定的涡结构，在一定程度上能够有效抑制高超声速边界层内不稳定扰动的发展，可以起到延迟转捩的效果。

1.3 不规则分布式粗糙度对高超声速转捩影响研究

近年来，Reda开展了许多不规则分布式粗糙度对高超声速边界层转捩影响的相关研究。在NASA的Ames高超声速弹道靶中，研究了不同几何构型模型(半球模型[52, 56]、圆锥模型[53-54]、球锥模型[54-56]等)表面分布式粗糙度对转捩的影响，获得了大量纹影图像和表面温度分布数据。研究发现，对于粗糙度高度小于层流边界层高度的情况，临界粗糙雷诺数相关法(Critical-roughness Reynolds Number)能够很好地反映粗糙锥体表面边界层的转捩过程，并且锥头钝度对粗糙度诱发的转捩开始阶段和发展阶段有重要影响。对于小钝度锥体，基于粗糙元高度的雷诺数Rek随粗糙度距顶点距离的增加而增大，且在一定情况下，随着自由流压力的增加，转捩起始位置前移，而Rek基本保持不变，如图8所示；与之相反，对于大钝度锥体，Rek随粗糙度距顶点距离的增加而减小，随着自由流压力的增加，转捩起始位置前移，且Rek逐渐增大[54]，如图9所示。除此之外，Wilder等[56]还模拟了飞行器登陆火星的气流条件，分析了二氧化碳(CO2)对分布式粗糙度主导转捩的影响。实验发现，在CO2气流条件下，Rek要比空气条件下偏小。

图8 小钝度锥模型及其纹影图(Ma=10)[54]

Fig.8Small-bluntnessmodel, (a)mountedinlaunchsabotand(b)modelinflightatMa=10[54]

图9 大钝度锥模型及其纹影图(Ma=10)[54]

Fig.9Large-bluntnessmodel, (a)mountedinlaunchsabotand(b)modelinflightatMa=10[54]

在激波风洞中，Irimpan等[57]研究了马赫数8.8、单位雷诺数1.98×106/m的来流条件下表面粗糙度对球体壁面热流的影响。研究发现，球体前部的粗糙度会降低模型表面传热性能，其原因可能是由于粗糙空腔中涡旋的持续存在推迟了转捩。Irimpan进一步分析实验模型的热通量数据，发现大范围的粗糙度使得球体的前体产生了多重空腔效应，如图10所示。粗糙度形成的空腔可通过捕获大尺度漩涡来抑制边界层的不稳定性，将其隔离、限制在这些空腔中，直到更下游区域，漩涡才开始脱落。因此，粗糙表面空腔上方的分离剪切层比光滑表面情况的剪切层更加稳定。

图10 粗糙表面多腔效应和涡旋动力学效应[57]

Fig.10Illustrationofthemultiple-cavityeffectandvortexdynamicsoveraroughsurface[57]

Giovanni和Stemmer[58]采用直接数值模拟(DNS)方法研究了钝头体上展向周期分布式粗糙度和随机分布式粗糙度引起的不稳定性机理。基于Ma=5.9来流条件下的半球状钝头体，分析了不同粗糙度后非定常扰动的发展。对于展向周期分布式粗糙度，其尾迹中存在两个主要的不稳定模态，分别对应于已知孤立粗糙元的对称和反对称模态；对于随机分布式粗糙度，在钝头体上观察到流动在经过不规则粗糙壁面时，流线会出现沿横向的弯曲，并在背风区域形成大小不一的分离区，这是一种新的由粗糙度诱导的横流不稳定性，如图11所示。

图11 随机粗糙壁面流线分布(绿色标记为分离区)[58]

Fig.11Streamlinedistributiononrandomroughwall(greenmarksseparationzone)[58]

在国内的研究中，张存波[59]利用数值模拟方法研究了分布式粗糙度的高度、波长、区域大小等参数对Ma=4.5的平板边界层扰动演化的影响。研究结果表明，经过粗糙度时，处在中性曲线以下的低频扰动会受到抑制，而处在中性曲线以上的高频扰动幅值会有所增长。

综上，由于粗糙元构型的复杂性和随机性，在不规则粗糙元对高超声速边界层转捩影响的研究中难以提炼出统一的理论模型。但由于不规则粗糙元模型更接近高超声速飞行器表面烧蚀、损伤的真实情况，对其诱导转捩的机理，还需开展更进一步的研究。

总的来说，在高超声速边界层中，无论粗糙元的形式如何(规则或不规则、孤立或分布、凸起或凹陷)，粗糙元后方的涡结构对其尾迹区流动的稳定性和转捩特性都起到了至关重要的作用。

2 转捩机理研究

高超声速流场的本质是高度非均匀、非定常的复杂三维流动，其中存在流动参数变化梯度很大的激波、滑流面、分离剪切层等。与低速和一般可压缩流动相比，高超声速边界层转捩的影响因素更多，不同影响因素之间还会发生相互作用从而产生新的影响，如图12所示[8]。因此，对高超声速边界层转捩机理的研究，往往需要把单个影响因素独立出来进行，尽量避免多因素相互干扰。粗糙元作为主要因素之一，其对边界层转捩机理的影响一直以来都是研究的热点。首先，感受性作为高超声速边界层转捩预测与控制的关键环节[60]，在国际上越来越受到研究人员的重视；其次，近年来众多学者对高超声速三维边界层转捩机理的研究表明：对于高超声速飞行器表面边界层转捩现象，横流失稳是主导因素[61-62]。本文将从粗糙元对高超声速边界层感受性问题以及横流失稳影响的角度，简述其在高超声速边界层转捩机理中的研究进展。

图12 高超声速转捩影响因素示意图[8]

2.1 感受性

为了系统研究和认识边界层转捩问题，人们把转捩过程分为4个阶段[63-64]。在其中第一个阶段，外界扰动进入边界层，并在其内部产生不稳定扰动，这就涉及边界层感受性问题[65-66]。外界扰动不同，边界层转捩的位置和机理也会不同。因此，如何确定外界扰动和转捩的定量关系，是感受性研究的关键问题。另外，影响感受性的因素很多，比如来流湍流度、声扰动、熵扰动、表面几何形状和壁面粗糙度等。根据扰动源的不同，可将感受性分为自由流扰动的感受性(声波、涡波和熵波)和壁面扰动源感受性(粗糙元、壁面震动、周期性抽吸和壁面加热等)[67]，如图13所示[68]。

图13 高超声速边界层自由流、壁面粗糙度扰动感受性[68]

Fig.13Thereceptivityinahypersonicflowinducedbyfree-streamandsurfaceroughnessdisturbance[68]

目前，关于低速边界层对粗糙元的感受性研究较多，包括离散式粗糙元、分布式粗糙度等[7,69]；而粗糙元对高超声速边界层转捩的影响虽是研究热点，但其影响机制仍未清晰[70-74]。通常情况下，高超声速边界层对粗糙元的感受性要比低速边界层复杂得多，其包含了粗糙元和来流声波、涡波的相互作用，涉及横流转捩、尾迹和瞬态增长等过程。在高超声速边界层感受性研究的理论方法中，均采用了一些特定假设条件，如渐进方法[75]、抛物化方程法(PSE)[76]、多模态法[77]等，其带来的影响并未经过相关实验检验，研究者大多是定性观察风洞来流扰动与边界层转捩雷诺数之间的相关性，风洞实验无法显示不同扰动模态如何通过激波以特定的色散关系进入到边界层内，并进一步触发边界层内扰动增长的过程[78]。另外，感受性处于高超声速边界层转捩的初始阶段，其扰动幅值非常低。一方面，为避免风洞喷管壁面湍流边界层产生的扰动对感受性研究的干扰，要求在研究中尽可能采用静风洞，而静风洞因其设计复杂、造价昂贵并未普及；另一方面，小幅值扰动及其发展超出了常规高超声速风洞实验技术的测量范围。因此，对高超声速感受性的实验研究十分有限。2001年前后，Maslov等在Ma=6来流中，测量了平板边界层对二维、三维声波的感受性系数，发现感受性系数与三维扰动波的迎角、幅值均无关，在0°迎角下，三维扰动的感受性系数约为二维扰动的1/5～1/6[79]。最近，Lee在北京大学Ф300mm高超声速静音风洞中，利用CO2瑞利散射流动显示和近壁粒子图像测速技术(Near-wall PIV)，研究了AC放电引入的人工扰动对来流马赫数6.5时的平板边界层转捩的影响，同时指出粗糙元通常对高超声速感受性有3种影响：粗糙元高度主要影响扰动振幅；粗糙元流向尺度通常影响扰动波频率；粗糙元几何形状影响扰动波波形(二维或者三维)[80]。

近年来，随着计算机硬件的飞速发展，针对粗糙元高超声速感受性的数值模拟研究取得了较大进步。Wang、Zhong和Fong等[81-82]通过直接数值模拟(DNS)分析了孤立粗糙元高度对高超声速边界层感受性的影响。研究发现，孤立粗糙元的高度会使扰动瞬时增大，且增长率随孤立粗糙元高度增加而变大。Duan等[83-84]也通过DNS方法研究了孤立粗糙元位置对高超声速转捩的影响，发现其位置的改变会直接影响慢模态在边界层中的传播，进而影响高超声速边界层的感受机理。在马赫数5.92的来流条件下，Duan使用高阶网格切割方法模拟了任意有限高度粗糙元和壁面抽吸对平板边界层的组合影响，其中粗糙元高度为当地边界层厚度的一半。图14展示了慢模态和粗糙元引起的压力波动，其中粗糙元放置于大约x=0.185m位置处。研究发现，流动经过边界层后会出现明显的压力波动。此外，当粗糙元位于同步点上游时，不稳定波的发展和没有粗糙元的情况相同；当粗糙元靠近同步点时，第二模态的不稳定性加剧；当粗糙元位于同步点下游附近，粗糙元会对不稳定的第二模态起到抑制作用。

图14 慢模态和粗糙元引起的压力波动[83]

Fig.14PressureperturbationsinducedbymodeSandsurfaceroughness[83]

与单个孤立粗糙元相比，对离散式粗糙元的高超声速边界层感受性的研究要少很多。Duan和Zhong[85]将上述方法应用于来流马赫数5.92条件下具有粗糙元阵列的三维平板边界层转捩的研究中。Balakumar[86]在尖锥模型上研究了二维离散式粗糙元对声波的感受性，发现靠近前缘处的离散式粗糙元能够降低慢声波的感受性，且粗糙元后的边界层比不带粗糙元的光滑圆锥更稳定；这与Fong等[87]通过数值模拟得到的圆锥同步点后的粗糙元可以抑制Mack第二模态的结论相吻合。Balakumar将离散式粗糙元置于同步点附近，发现能够提高Mack第二模态对涡波的感受性，但对快慢声波的感受性则没有影响。另外，粗糙元距离同步点的位置，以及粗糙元相对于当地边界层厚度的比例，是影响感受性过程的重要因素。

2.2 横流失稳

一直以来，对边界层转捩的理论分析主要采用流动稳定性方法，即：考虑给定主流流动条件下的边界层对外界扰动的感受性特征，主要研究不同种类的扰动在边界层内的放大或衰减过程[88]。高超声速三维边界层内存在多种失稳机制[89]：附着线失稳、前缘污染失稳、第一和第二模态失稳、离心Görtler涡失稳以及横流失稳。横流失稳属于无粘条件下的不稳定性，是高超声速飞行器表面三维边界层转捩的主导因素。

基于线性稳定性理论，横流行波模态的放大率要高于横流驻波模态。但是，由于横流驻波模态对粗糙度有很强的感受性，这种感受性给横流驻波模态提供了更高的初始振幅，弥补了其放大率的不足。因此，除了在来流扰动很强的条件下，横流失稳中的主导不稳定模态都是横流驻波模态[90]。在边界层中，随着横流驻波模态的振幅增长，会形成同向旋转的涡。这些旋涡和基本流的无粘流线近似重合，会对边界层造成很强的综合影响。随着旋涡振幅进一步增大，会造成主流的扭曲，在主流速度型上形成拐点[91-94]，如图15所示[94]。带有拐点的速度型会导致无粘二次不稳定性，产生小尺度的速度波动，使流动最终变成湍流。对可压缩横流失稳相关机理已有较多研究[95-99]，本文主要介绍粗糙元在横流失稳及控制中的研究工作。

图15 横流边界层速度型[94]

粗糙元对横流失稳的影响机理主要基于横流驻波对表面粗糙度的强烈感受性[100]。Saric等[101]和Radeztsky等[102]利用这一特性，在后掠翼实验中使用微米尺寸的圆形离散式粗糙元阵列，激发出具有固定展向波数的横流驻波模态，并证实了在边界层中只出现了相同展向波数的横流模态(理论上，该波数的高次谐波也有可能出现，但低于该波数的横流驻波模态总是被完全抑制)。这些观测结果给出了粗糙元横流控制的一种新思路，即：能否通过粗糙元激发出一种小振幅横流驻波模态来控制转捩。其关键是：引入的横流驻波扰动模态的波数，要高于自然情况下主导转捩的横流驻波模态的波数，才能保证没有扰动能量通过非线性相互作用进入到低波数、高放大率的扰动模态中。Saric等[101]通过实验发现，使用高度为50μm的半球形点状表面粗糙元能够使后掠翼上的转捩延迟。随后，通过粗糙元、等离子体等对超临界机翼的横流失稳进行控制，发现粗糙元和等离子体可以改变基本流的形态，其激励出的次不稳定横流波可抑制先前最不稳定横流波的发展，从而最终抑制横流失稳[103]。

由于在高超声速构型设计中能够提供不同影响因素的丰富信息，圆锥被证明是研究高超声速边界层三维转捩及横流失稳问题的最理想外形[104]。因此，关于粗糙元对高超声速横流失稳影响的研究主要集中于带迎角的圆锥。带迎角的锥形流场会产生和流线垂直的压力梯度，如果设计得当，该压力梯度就会导致横流的产生。Craig和Saric[105]对Ma=6来流条件下带迎角圆锥的横流失稳进行了研究，发现横流驻波和行波模态的增长和发展与之前在低速实验中观察到的情况很一致。但是，当振幅饱和后，Ma=6来流条件下会观测到二次不稳定波的发展，这种差异足以影响到最终的转捩。因此，在高超声速时，完全基于低速风洞实验的横流转捩控制手段是无效的。

在Ma=3.5时，Schuele等[106]用半锥角为7°的圆锥进行了风洞实验，并使用了离散式粗糙元，其激发出的次不稳定定常横流涡使转捩位置延迟了35%，如图16所示(图中m表示azimuthal wave number)。最近，Corke等[107]将Schuele的实验扩展到了Ma=6来流条件，由于粗糙元引入了次不稳定扰动波，抑制了最不稳定扰动波的发展，因此转捩延迟了25%。此外，由于Corke的实验是在常规高超声速风洞中进行的，实验中观测到了横流驻波和行波之间的相互干扰，Corke推测这可能是常规高超声速风洞中导致转捩提前的原因。

图16 不同粗糙元条件下的转捩位置[106]

Swanson等[108]对半锥角7°、迎角6°的圆锥在静风洞中进行了来流马赫数6的实验。研究发现，在高噪声来流中，转捩趋向于背风面，通过在锥尖附近放置粗糙元可使转捩前移。在低噪声和静来流中，采用温度敏感漆(Temperature Sensitive Painting，TSP)均观测到了横流驻波，但没有观察到转捩现象。在低噪声条件下，粗糙元对驻波没有产生明显影响，增大风洞噪声对驻波也没有任何影响。van den Kroonenber等[109]使用相同的模型，利用红外热成像法获得了圆锥全局传热的信息。研究发现，当单位雷诺数在6.5×106～11.3×106/m之间时，横流驻波才能够被观测到。在圆锥尖端附近放置离散式粗糙元时，对驻波没有明显影响。在Mach 6静风洞中，Chynoweth等[110]也利用TSP技术对粗糙元控制尖锥的横流失稳现象进行了研究，结果如图17所示。可以看出，在低单位雷诺数条件下(8.1×106/m)，粗糙元会引起较大振幅的横流驻波(与光滑壁面相比)，从而促进边界层横流失稳；而在较高单位雷诺数条件下(10.4×106/m)，则会引起较小振幅的横流驻波，从而抑制边界层不稳定性。目前，对这一现象还没有清晰的解释。

图17 不同单位雷诺数对粗糙元抑制转捩的影响[110]

Fig.17EffectofReynoldsnumberonsuppressingtransitionbyroughnesselements[110]

3 NHW风洞相关研究进展

目前，已有多种新兴测量技术应用于高超声速转捩研究[111-113]，如PIV、PLIF、NPLS等。虽然它们的测量精度较高，但是均存在近壁剪切力大、粒子均匀播散困难、校准和实验方法复杂等问题。油膜干涉法是一种适用于边界层转捩风洞实验的传统的非接触测量方法。该方法具有测量面积大、测量精度高和实验成本低等特点[114-116]。近年来，本文作者将油膜干涉法应用于边界层转捩风洞实验研究，在低速风洞[117-118]、高速风洞[119-121]中取得了一定成果，在南京航空航天大学高超声速风洞(NHW)中也开展了三维表面凸起粗糙元诱导高超声速平板边界层转捩的实验研究。

3.1 实验设备及模型

NHW是一座喷管出口直径Φ500mm的高压下吹、真空抽吸暂冲式高超声速风洞，实验名义马赫数为4、5、6、7和8，真空球容积为650m3，每车次实验时间可大于10s[122]。试验段及真空驻室上方有一个350mm×350mm的观察窗，可通过观察窗使用CCD相机或高速摄像机对模型和流场进行相关光学测量。

在高超声速边界层转捩风洞实验研究中，来流噪声水平一直是一个重要的参数。目前的主流研究设备分两种，第一种是高超声速静风洞(如普渡大学Mach 6静风洞、北京大学Mach 6静风洞、国防科技大学Mach 3～6低噪声风洞)，通过一系列降噪措施(如抛光壁面、抽吸等)，使来流噪声水平低于0.1%(来流压力脉动/平均压力)。但静风洞建造成本高、来流马赫数一般有限制，难以大规模推广。第二种是传统高超声速风洞，其来流噪声水平一般要比高超声速静风洞高一个量级(具体数值与来流总压、来流马赫数、测量位置等参数密切相关)。本文涉及的南京航空航天大学NHW风洞实验均为高超声速转捩数值方法和实验技术的验证性实验，并未实时监测来流噪声水平。根据实验来流参数，由文献[123]可知，在来流总压约4×105Pa、名义马赫数5的条件下，NHW风洞的噪声水平低于2.5%。

其他实验设备包括单色光源、高速相机以及分析纯度硅油。其中，单色光源采用单色钠灯和单色LED灯，波长均为589nm；相机为PCO公司的S4高速相机，实验帧率为100帧/s(远低于其极限帧率1000帧/s)；硅油选用阿拉丁公司的粘度为50cst的高纯度分析级硅油。

油膜干涉实验模型为平板模型，长190mm，宽150mm，前缘为倒角20°的尖楔形。三维粗糙元为圆柱形孤立粗糙元，直径3mm，高度1.6mm，距离模型前缘50mm，中心位于平板模型沿流向的对称面上。

3.2 实验结果及分析

实验名义马赫数为5，来流马赫数为4.97，来流总压p0=3.909×105Pa，总温T0=516K，单位雷诺数为4.7×106/m。在进行模型表面尺寸标定后进行风洞实验，测量范围为距离平板前缘约50～130mm的局部区域。为比对验证实验结果，采用基于有限体积的高阶紧致格式(CFVM)并行算法[124]，对相同来流条件下的光滑平板模型以及带三维圆柱形孤立粗糙元的平板模型进行数值模拟。

图18为风洞流场中光滑平板模型油膜干涉图像，以及由此计算出的沿流向中心线上相应位置的表面摩擦阻力系数Cf和数值模拟结果的比较。可以看出：硅油在剪切力作用下向下游延展，形成硅油薄膜，经单色钠光照射，产生清晰的干涉条纹；模型表面中心线处的摩阻系数Cf沿流向逐渐减小，且风洞实验结果与层流数值模拟结果吻合；Cf数值约为0.001，表明当前平板边界层流动处于层流流态，在可视范围内没有发生自然转捩。

图19为风洞流场中带三维圆柱形孤立粗糙元的平板模型油膜干涉条纹，以及数值模拟得到的Cf分布和对称面上密度分布图。对比图18可见，三维圆柱形孤立粗糙元后的干涉条纹比光滑平板模型的宽得多。由密度分布图可知，这是由于三维粗糙元后方流场中形成了尾涡，引起平板边界层中强烈的扰动和剪切作用，使层流边界层转捩为湍流。由数值计算结果可知，粗糙元对下游边界层流场的影响程度以x=100mm为界线分为两个部分：在x=100mm之前，粗糙元后中心线上下有两个对称区域A和B，该区域Cf较大(比相同x位置的中心线上的Cf更大)，这与油膜干涉图像中的1、2、3区域相吻合；在x=100mm之后，中心线上下两侧区域的Cf逐渐减小，这与油膜干涉图像中展向条纹连续性变得更好的趋势相吻合。

(a) Ma=5条件下光滑平板表面油膜干涉条纹图像

(b) 表面摩擦阻力系数实验结果和数值结果对比

Fig.18Oilfilminterferenceimageofsmoothflatplateandcomparisonofsurfaceskinfrictioncoefficient

(a) Ma=5条件下粗糙元尾迹区油膜干涉条纹

(b) Ma=5条件下基于DNS的粗糙元尾迹区摩擦阻力系数分布

(c) Ma=5条件下基于DNS的粗糙元中心剖面密度分布

Fig.19Oilfilminterferencefringesandnumericalsimulationresultsafter3Dcylindricalisolatedroughnesselements

以上研究表明，油膜干涉测量技术可以应用于粗糙元诱导高超声速边界层转捩的研究中。下一步，可结合NHW噪声水平的实时监测，对不同形状、不同高度、不同间距等的离散式粗糙元诱导转捩的效果和机理进行深入研究。

4 结束语

国防和民用航空航天领域对高超声速飞行器及高超声速技术发展需求日益强烈，对高超声速边界层转捩问题的研究也更加迫切。但转捩问题的复杂性、研究手段的局限性以及现有理论的不完善，决定了转捩研究将是一个长期而艰难的过程。在这一过程中，转捩机理是研究的重点、难点和根本；而转捩预测和转捩控制方法是研究的主要目的，直接支撑着新型高超声速飞行器的研制。作为影响高超声速边界层转捩的诸多因素之一，粗糙元是转捩控制的主要手段，必将长期作为研究热点。

现有研究表明，精心设计的离散式粗糙元可以推迟转捩。研究者不仅应继续注重规则粗糙元高度/深度、形状等参数对诱导转捩效果及机理的相关研究，更应重视离散式粗糙元间距、不规则粗糙元等对高超声速转捩的影响。另外，对烧蚀、物理损伤、机械加工等造成的飞行器表面不规则的凸起或凹陷的研究，更加具有工程价值。

粗糙元影响高超声速边界层转捩机理的研究已取得了一定成果。大多数研究者认为：粗糙元会在高超声速边界层内产生具有流向涡度的尾涡，足够高度的粗糙元将产生激波，尾涡和激波的作用会增加边界层内的不稳定性。一方面，边界层内的粘性效应不足以使这种不稳定性在流动下游消散；另一方面，随粗糙元参数变化的流向涡会通过与自由流扰动的相互作用(感受性)、横流失稳、Görtler失稳以及瞬态增长机制而发展，最终导致层流转捩为湍流。目前，对高超声速边界层感受性、横流失稳的研究很少[8]。在感受性问题中，要注重针对粗糙元诱导的不稳定波激发路径的理论和实验研究；而在横流失稳中，应重点关注三维边界层中诸如驻波、行波、二次失稳、第二模态等多种扰动模态的辨识和相互干扰问题。

高超声速流动存在区别于低速、一般超声速的明显特征，在低速或一般超声速边界层转捩中出现的现象或适用的规律，在高超声速条件下并不存在或不适用。有研究表明，在低速、一般超声速中应用的转捩控制手段，在高超声速条件下并不完全有效。但是，不能将高超声速边界层转捩的研究局限于高超声速范围之内，使之与低速、一般超声速流动中的转捩研究割裂开来。这是由于高超声速飞行器近壁面边界层、驻点附近的马赫数很低，将粗糙元布置在这些位置，控制效果更加明显。例如，航天飞机和高超声速导弹鼻锥处粗糙元后的流动，也属于高超声速转捩研究的内容，具有重要的研究价值。

总而言之，高超粗糙元形式众多，本文仅简要综述了表面凸起、凹腔、多孔壁面、分布式粗糙度的相关研究。各种粗糙元对高超声速边界层转捩影响的机理和规律尚不完全清楚，需要通过理论、数值方法以及高超声速风洞实验技术的发展和进步，并与飞行试验数据验证相结合，循序渐进地开展更加深入的研究。