基于PSO自动确定聚类数目的FCM算法

肖剑文 周亦敏

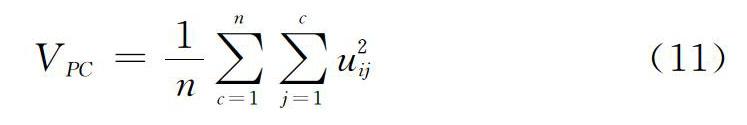
摘要：模糊C均值聚类是聚类分析中应用最广泛的算法之一，但是聚类数目需要人为预先设定，在实际应用中有极大的局限性。提出一种自动确定聚类数目的基于粒子群的模糊C均值聚类算法，通过对不同聚类数目进行试验，利用添加粒子阈值向量自动确定最佳的聚类数目。在预设的最大聚类数目内随机分割数据集，利用重构准则重新构建初始值，以此克服需要事先设置聚类数目的模糊C均值缺点。利用有效性函数评估算法性能，试验结果表明，该算法能自动找到最优聚类数目，聚类效果很好。

关键词：模糊C均值;粒子群;粒子阈值;重构准则;有效性函数

FCM Algorithm Based on PSO for Automatically Determining the Number of Clusters

XIAO Jiao wen，ZHOU Yi min

（School of Optical electrical and Computer Engineering，University of Shaghai

for Science and Technology， Shanghai 20093， China）

Abstract：Fuzzy C means clustering is one of the most widely used algorithms in cluster analysis. However， the number of clusters needs to be preset manually， which has great limitations in practical applications. In this paper， a particle swarm optimization fuzzy C means clustering algorithm is proposed to automatically determine the number of clusters. This algorithm uses the additive particle threshold vector to automatically determine the optimal number of clusters by experimenting with different cluster numbers. The algorithm firstly randomly divides the data set within the preset maximum number of clusters， reconstructs the initial value by using the reconstruction criterion， and overcomes the shortcomings of the fuzzy C means that need to set the number of clusters in advance， and uses the validity function to evaluate the algorithm. The experimental results show that the algorithm can automatically find the optimal number of clusters and achieve a good clustering effect.

Key Words：fuzzy C means ;particle swarm optimization; particle threshold ;reconstruction criterion;validity function

0 引言

與分类[1]的监督算法不同，聚类[2]属于无监督算法，指在没有先验知识的情况下将数据分为多个类或簇，同一类中的数据具有较高的相似性[3]，不同类之间的数据相似性尽可能低。传统的聚类分析都是把数据硬性地划分到某一类中，而现实的事物大都具有模糊性，即事物之间的划分界限不明显。模糊聚类[4]方法中每个样本与聚类中心点之间存在着隶属关系，展示了类属的模糊性，能更好反映现实世界。

聚类分析是无监督模式识别[5]的重要研究课题之一。模糊聚类能更客观地反映现实世界，因为它建立了样本到类的不确定性描述。传统模糊聚类算法的主要缺点是无法自动确定最优排序的聚类数，为了准确完成聚类需要事先确定聚类数目。但是对于一些线性不可分的数据、分布较为复杂的数据，即使给定了最优的聚类数目也很难得到理想的聚类效果，作为模糊聚类典型代表的模糊C均值聚类（FCM）[6]也有此缺点。

当前通常采用有效性函数[7]分析聚类结果以此确定群集的最佳数目，其中有效性函数分为两类：①基于数据集分区的模糊方法;②通过基于数据集的几何图元。其中具有代表意义的方法有以下4种：

（1）Bedzek[8]提出的分区系数（Partition Coefficient），它的目的是测量群集之间的重叠程度，其值越大代表聚类效果越好。

（2）香农[9]提出的分类概念熵，索引值越小代表聚类效果越好。

（3）Win[10]提出的有效性函数 V kwon，是对谢本尼Xie-Beni指数的一种改进。它能有效抑制指数值的下降使其不再为0，其值越小代表聚类效果越好。

（4）Bensay[11]提出的有效性函数 V bsand，其值越小代表聚类效果越好。

但是通过分析结果确定聚类的最佳数目使计算开销大大增加，对此本文提出了一种新的自动确定聚类数目的基于粒子群（PSO）的模糊C均值聚类算法（FCM），该算法能自动确定最优聚类数，并通过重构函数大大降低计算开销。为证明该算法的有效性，通过在UCI机器学习库[12]的5个数据集上进行MATLAB仿真模拟实验，同时通过有效性函数对聚类结果进行验证。结果表明，自动确定聚类数目的基于PSO的FCM算法能够自动确定最优聚类数目，聚类效果很好。

1 粒子群算法与模糊C均值聚类

1.1 粒子群算法（PSO）

粒子群算法（PSO）由Eberhart和Kennedy[13]设计的一种群搜索算法。该算法通过模拟鸟群捕食行为进行设计。假设区域里只有一块食物（即优化问题中所讲的最优解），鸟群的任务是找到这个食物源。鸟群在整个搜寻过程中通过相互传递信息告知其它鸟自己的位置，通过这样的协作判断找到的是不是最优解，同时也将最优解信息传递给整个鸟群，最终整个鸟群都聚集在食物源周围，即找到最优解，问题收敛。

在下一次迭代中，粒子的速度和位置更新公式如下：

其中，i=1，2，…，N，第i个粒子的速度为V i=（v 1，v 2，…，v d），第i个粒子的位置为X i=（x 1，x 2，…，x d），r 1，r 2为两个随机数，满足[0，1]之间的随机均匀分布，并且两个数之间相互独立。t为当前迭代的次数，c 1，c 2是学习因子，为两个非负的常数，w为递减的惯性因子。

1.2 模糊C均值聚类（FCM）

模糊聚类允许一个数据属于两个或多个聚类。 FCM算法是一种迭代分区聚类技术，由Dunn[14]引入并由Bezdek[15]扩展。 FCM是一个非常标准的最小二乘误差模型，是早期非常流行的非模糊C means模型的推广，该模型可以生成硬数据集群。通过加权迭代目標函数的最小化平方误差组的和得到最优结果。假设 X={x 1，x 2，…，x n}是要进行聚类的数据集，每个数据具有m个属性，标准的模糊C均值聚类将每个对象x i（1≤i≤N）分配给具有ac×N隶属度矩阵[16]U = {u ij}的第c个聚类。 u ij表示属于第i组的第j个对象的隶属度。

标准模糊c均值方法由下列等式定义：

因此，标准的模糊C均值聚类算法目标是为了计算隶属度矩阵以及聚类中心点C={c i，c 2，…，c c}。给定数据集X，标准模糊c均值算法随机初始化隶属度矩阵，然后通过最小化目标函数J m更新隶属度矩阵和聚类中心，其目标函数如下：

其中m为模糊因子，一般取值为2，d ik表示x k和v i之间的距离，通常是欧式距离：

FCM算法步骤如下：

（1）初始化参数，包括初始化模糊因子 m，给定聚类中心点个数c，最大迭代次数T max以及最小迭代误差 ε，令初始迭代次数t=1。

（2）初始化隶属度矩阵U=[u ij]。

（3）利用隶属度矩阵Ut计算聚类中心点C，公式如下：

（4）利用下式更新隶属度矩阵 Ut+1 ：

（5）判断算法是否满足终止条件，满足则终止算法输出结果，否则令 t=t+1 ，返回步骤（3）。

2 编码方式

2.1 粒子编码

粒子是2×c矩阵，其中c是预定义的最大聚类数目。 第一行代表中心， 第二行中的每个值控制第一行中每个中心的激活。

X i=x i 1，1x i 1，2…x i 1，c t i 2，1t i 2，2…t i 2，c

其中， x i 1，c 代表粒子在类c中的位置，其范围在[ x min， x max]之间。 t i 2，c 为粒子的阈值，范围为[0，1]。 如果阈值大于0.5则激活聚类中心，否则它将被停用。

2.2 速度编码

速度矩阵与位置矩阵具有相同大小，设置速度的范围为[ v min， v max]，速度的所有值都应该在 v min和 v max之间，因此粒子的速度表示为：

V i=v i x1，1v i x1，2…v i x1，c v i t2，1v i t2，2…v i t2，c

同样， c 是最大簇数。 第一行是中心的速度，第二行是阈值的速度。

2.3 解码

X=（x 1，x 2，…，x n）是具有d维的数据集， 可用公式（8）将聚类中心解码为C=（c 1，c 2，…，c c） 。

2.4 有效性函数

聚类有效性分析目的是为了评估聚类效果以找到最合适的分类数目，因此采用有效性函数评估聚类结果，通过结果分析发现最佳的聚类数目。类内紧凑度和类间分离度是衡量数据聚类效果的两个常用标准。常规方法是使用不同的聚类数目迭代运行算法，通过有效性函数判断最佳的聚类数目，下面是常用的模糊聚类中的有效性函数：

（1）最小平方误差（SE）[17]：

其中，x i是具有d维属性的数据点，c j是第j类数据集的值，‖x i-c j‖是x i和c j的欧几里得距离， J m最小时聚类效果最好。

（2）分区系数（PC）[18]指数：

当PC值越大时聚类效果越好。

（3）分区熵（PE）[19]索引：

其中 b 是对数基数， PE越小聚类效果越好。

（4）XB[20]指标：

XB值越小聚类效果越好。

3 自动确定聚类数目的FCM算法

通过以上分析，基于PSO得到自动确定聚类数目的FCM算法，具体步骤如下：

（1）输入数据集 X={x 1，x 2，…，x n}，聚类数目c，模糊因子c。

（2）随机初始化一个粒子群，设置t=1。

（3）利用式（1）更新每个粒子速度。

（4）利用式（2）更新每个粒子位置。

（5）更新局部最优值和全局最优值。

（6）计算分区矩阵U。

（7）判断是否满足算法终止条件。满足进入步骤（8），否则返回步骤（3），同时令t=t+1。

（8）利用全局最优矩阵重新构造原始数据。

（9）计算重构误差。为了使用一致的方法评估4个不同的有效性函数，这里使用RC重构标准[21]，使用簇原型和分区矩阵重建原始数据， X={x 1，x 2，…，x n} 计算公式如下：

重构完成后，使用式（15）评判重构值和原始值之间的平方误差：

（10）选择重构误差最小的分区矩阵和中心。

4 试验结果与分析

本试验测试的仿真环境如下：CPU为AMD 四核 FX 7500 up to 3.3GHz，8G内存，MATLAB2010编程环境，表1列出了算法参数。

为验证算法性能，选择来自机器学习数据库UCI中的数据集进行试验，数据集的详细描述信息见表2。

使用上面提到的4种有效性指标验证试验结果，通过式（10）-式（13）使用所提算法计算数据集的重构误差，聚类数目的取值范围为2-9，粗体值是每个度量具有不同簇编号的最小重建误差。8组试验中的6组表明 c =2是最佳聚类数目，试验结果见表3。

对提出的算法进行验证，在50次运行中测试所提算法并计算表4列出的平均最佳数据数目，括号中的值是标准误差。结果表明，本文提出的算法可获得最优的聚类数目，实验结果如表4所示。

5 结语

本文提出了一种自动确定聚类数目的基于PSO的FCM算法，以克服传统聚类算法中需要人为输入聚类数目的缺陷。利用阈值向量控制聚类的数量，同时通过迭代模糊分区的方法解决聚类问题。使用来自UCI机器学习库的5个数据集进行模拟仿真实验，结果表明本文所提出的算法能够找到最优的聚类数目，得到很好的聚类结果。

本文不足之处：由于引入了粒子阈值向量控制聚类数目，而算法初始聚类中心是随机选取的，在一定程度上影响算法的执行效率。为了避免最佳聚类数目不在所设定的范围内，需要设定较大的最大聚类数目以保证最佳聚类数目包含其中，这需要一定的先验知识作为基础，这都是有待进一步研究与完善的地方。

参考文献：

[1] 刘红岩，陈剑，陈国青.数据挖掘中的数据分类算法综述[J].清华大学学报：自然科学版，2002，42（6）：727 730.

[2] 伍育红.聚类算法综述[J].计算机科学，2015，42（6）：491 524.

[3] GRAVES D，PEDRYCZ W.Kernel based fuzzy clustering and fuzzy clustering：a comparative experimental study[J].Fuzzy Sets and Systems，2010，161（4）：522 543.

[4] 王春花.基于模糊C 均值聚類的图像分割技术研究[D].大连：辽宁师范大学，2008.

[5] 程于洁，肖华瓶.模式识别发展及现状综述[J].好家长，2018（84）：68 69.

[6] BEZDEK J C. Pattern recognition with fuzzy objective function algorithms[M]. New York： Plenum， 1981.

[7] 邱学芹.模糊聚类算法及其聚类有效性的研究[D].青岛：青岛理工大学，2010.

[8] BEDZEK J C. Cluster validity with fuzzy sets [J]. Journal of Cybernetics ，1973，3 （3）：58 72.

[9] SHANNON C E. A mat hematical theory of communication[J] .Bell Syst Tech ，1948，XXVII（3）：379 423.

[10] KWON S H.Cluster validity index for fuzzy clustering[J] .Elect ronics Letters ，1998，34（22）：2176 2177.

[11] BENSAID A M.Validity guided（re） clustering with applications to imgae segmentation[J].IEEE Transaction on Fuzzy Systems ，1996 ，4（2） ：112 123.

[12] ASUNCION A， NEWMAN D J. UCI machine learning repository[EB/OL]. http：//www.ics.uci.edu/mleamlMLRepository.html.

[13] EBERHART R C，KENNEDY J. A new optimizer using particle swarm theory[C].Proceedings of 6th Symp of Micro Machine and Human Science 1995： 29 43.

[14] DUNN J C.A fuzzy relative of the ISODATA process and its use in detecting compact well separated clusters[J].Journal of Cybernetics ，1973（3）：32 57.

[15] BEZDEK J C.Pattern recognition with fuzzy objective function algorithms[M]. New York：Plenum Press，1981.

[16] 朱書伟.基于群体智能的多目标聚类算法研究[D].无锡：江南大学，2016.

[17] BEZDEK J C. Cluster validity with fuzzy sets[M]. New York：Plenum Press ，1973：58 73

[18] BEZDEK J C .Pattern recognition with fuzzy objective function algorithms[M]. New York：Plenum Press， 1981.

[19] BEZDEK J C， CORAY C， GUNDERSON R，etal.Detection and characterization of cluster substructure I. linear structure： fuzzy c lines[J].SIAM Journal on Applied Mathematics， 2006：40（2）， 339 357.

[20] PAL N R， BEZDEK J C.On cluster validity for the fuzzy c means model[C]. IEEE Transactions on Fuzzy Systems， 1995， 3（3）：370 379.

[21] PEDRYCZ W ， DE OLIVEIRA J V.A development of fuzzy encoding and decoding through fuzzy clustering[J].IEEE Transactions on Intrumentation and Measurement， 2008，57（4）：829 837.