考虑排污权交易的有限理性竞争博弈模型研究
张骥骧
摘要:从博弈论的角度对有限理性企业进行定价策略研究。依据排污权交易市场容量随着时间发生变化的特点,修正了传统的Bertrand 竞争模型,得到两个企业同时博弈的排污权交易动态Bertrand模型及其所对应的价格均衡解。并对均衡解进行稳定性分析,数据模拟。使得Bertrand 竞争模型能够适用于更为实际的竞争情形。
Abstract: The price fixing strategy of bounded rationality enterprise discharge right from the point of game theory is discussed. In view of the property that the market capacity for emission trading varies with time, we propose a modified dynamical Bertrand model with emission tracing's simultaneous-move game. Find out the equilibrium game theory, analyzes its stability and display the simulating data. Our analysis shows that the new model is extension to the traditional one, and it can apply to more practical competition case.
關键词:有限理性;排污权定价;博弈论;Bertrand模型
Key words: bounded rationality;emission right pricing;Game theory;Bertrand model
中图分类号:F752.69 文献标识码:A 文章编号:1006-4311(2018)06-0101-03
0 引言
寡头垄断,一种由少数卖方(寡头)主导市场的市场状态,是一种普遍存在的市场结构。1838年,法国经济学家古诺(Cournot)提出了在双头垄断市场情形下的关于产量决策的古诺模型。1883年,伯川德(Bertrand)研究了双头进行价格竞争的博弈模型。Cournot模型和Bertrand模型是两个经典的竞争模型。自从Bertrand提出价格竞争相对于数量竞争来说,具有更低的均衡价格和更高的均衡产出以来,两个模型的比较分析就一直是寡头竞争研究的重点之一。目前,这两个模型已经成为经济学中的经典模型,并得到了不断的发展和改进。例如,文[1]、文[2]、文[3]研究了一定时期内寡头垄断者之间进行多次产量博弈的动态古诺模型,给出其最优产量解,并分析了系统的稳定性。文[4]把有限理性、溢出效应以及非线性成本函数引入经典Cournot模型中,发现寡头的理性和溢出效益在博弈动态地趋于Nash均衡过程中起着非常重要的作用。文[5]对有限理性动态古诺模型进行了改进,并将其引入到广告市场中,对其的演化过程进行了分析。文[6]的模型主要考虑的是在市场信息不对称的情况下,理性层次不同的个体因为掌握的信息量以及对市场的反应能力不一样采用完全不同的竞产策略,一方采用延时有限理性竞产决策另一方采用最优反应。文[7]建立了适用于耐用品市场的动态古诺模型。文[8]研究两个企业同时博弈的耐用品动态Bertrand模型。文[9]探讨了同时进入且同时价格博弈的Bertrand竞争模型,并扩展到重复博弈的情形。文[10]以彩电行业为例,分别从产品特征、产业生命周期等6大方面揭示了易发生价格竞争的产业特征,并提出产业内企业可行的价格战应对策略。
对于特定的排污权交易市场而言,传统动态古诺模型中的市场容量保持不变的隐含性假设并不成立。对于排污企业产品的市场容量随着时间变化的特点在价格博弈中也同样适用。而且价格竞争也并不仅仅维持一个博弈阶段。为此,本文将传统的Bertrand竞争模型扩展到动态博弈中,并具体到排污权交易企业产品市场中加以研究,由此初步建立了两个企业同时博弈的有限理性企业动态Bertrand模型。
1 模型
假定1:双寡头垄断不完全竞争市场中有两个企业j(j=1,2)分别生产产品j。每个企业选择自己的价格Pj以实现自身利润最大。两个企业的需求函数分别为:q1=a-p1+b1p2,q2=a-p2+b2p1,其中p1,p2分别为产品的市场价格,a、b1、b2为非负系数。a为市场容量,b1、b2分别为产品顾客需求影响系数。成本函数C1(q)=C1q1,C2(q)=C2q2具有线性形式,C1>0,C2>0。企业i的污染治理成本是产量的线性函数即:Di(q)=diqi,其中di为企业i的边际污染治理成本。
假定2:生产过程中产生污染,且污染物的数量记为Eiqi,其中Ei为企业i的污染生产系数,此外,企业i的污染治理水平也是与产出水平qi线性相关,记为Giqi,其中Gi为污染治理系数。则企业i的总排污量为Eiqi-Giqi。
假定3:y0(n)为免费分配到的初始排污权。企业i排污权的交易量为Eiqi-Giqi-y0。排污权的交易价格为M,企业1为排污权交易价格的接受者。(假设企业1所缺的部分刚好由企业2提供即:M(E1q1-G1q1-y0)=M(y0-E2q2-G2q2))。
当条件满足(9)时E*局部稳定的。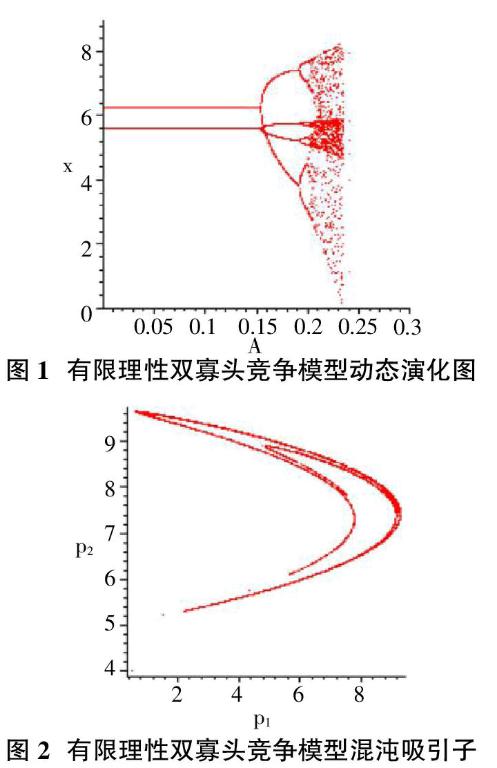 endprint
endprint
价格调整速度跟A企业的决策相关,企业为了追求高利润,随时可能改变自己的价格调整速度(策略机制);在寡头竞争市场中,两家企业同时调整策略,势必会影响整个市场的发展动态,会导致价格竞争极其复杂的现。下面根据动力系统相关理论,对模型进行分析得到其动力学行为的完整结论,并数值模拟出此类寡头竞争的动态演化。
3 数据模拟
为了更直观地了解式(5)的动态行为,对双寡头竞争模型(5)进行数据模拟.描绘出系统的动态演化过程和对初始条件的敏感依赖性等图。
对初始条件的敏感依赖性也是混沌现象重要特征,为验证系统(5)是否对初始值具有敏感依赖性,图3分别绘制出初始值为(p10,p20)和(p10+0.00001,p20),关于产量p1和时期t的关系图。可以看出初始产量的微小变动都会对博弈结果产生巨大的影响。
根据以上的分析可以看出:有限理性企业的价格调整速度快慢对模型系统的稳定性有显著影响,一旦产价格调整速度超过某一临界值,系统将表现出分叉、混沌等复杂的动力学现象。
4 结论
排污权交易制度利用市场机制实现污染物的排放控制。传统的排污权交易模型在理论上假设了无交易成本的、正规的排污权交易市场,但从实践来看与理想假设相差甚远,由于在排污权交易市场运作过程中存在着信息不充分交易不频繁、逐案谈判等问题,交易费用相当高昂,从而降低了排污权交易的市场成交量、压抑排污权交易的供給与需求。我国市场交易机制不够完善,更需要深入分析排污权交易对市场结构的影响及其导致的污染治理效率改变等问题,以采取能够促使交易市场形成并完善的措施。
为了更直观的研究排污权价格,本文建立了引入有限理性的双寡头排污权Bertrand竞争模型,对此模型进行了稳定性分析,给出了完整的结论,并对博弈的过程进行了数值模拟。结果表明当调整价格的相对速度参数发生变化时,均衡点失去稳定性,竞争双方价格的调整对最终结果产生巨大的影响,从而使市场进入混沌状态。对于较低的调整反应速度,竞争会趋向唯一的均衡,但随着调整反应的速度的增加,均衡点稳定性会发生变化,分支、混沌等复杂现象将出现。分叉或混沌状态下的系统对于双寡头并非都是不利的,在某些条件下企业可以从中获利,关键看系统波动是由哪个企业引起的。系统一旦进入到混沌状态,任何初始条件的细微变化都会给最终竞争结果带来巨大的影响,使得双寡头都无法对长期的价格决策进行预测调整。所以对于具有有限理性的双寡头企业博弈,要不断的注意企业所处环境的变化,适时地调整企业自身的发展目标,使得博弈均衡的稳定区域扩大,尽量避免价格竞争进入混沌的不可预测状态。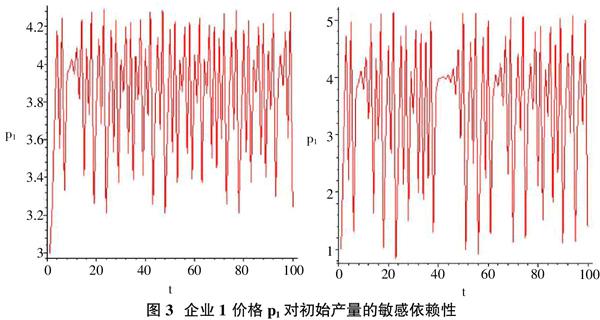
由于排污权市场的特殊性,本文对传统的Bertrand竞争模型进行改进。新模型是对传统模型的进一步扩展,并且新模型的假设条件更为灵活,能够适用于更广泛、更实际的情形。
参考文献:
[1]Agiza H N, Hegazi A S. Elsadany A A. Complex dynamic sand synchronization of a duopoly game with bounded rationality [J] .Math. Compute. Simulation, 2002, 58 (2):133-146.
[2]Agiza H N, Hegazi A S, Elsadany A A. The dynamics of Bowelys model with bounded rationality [J]. Cha2os, Solutions and Fractals, 2001, 12: 1705 - 1717.
[3]Bischi G I, Naimzada A. Global analysis of a dynamic duopoly game with bounded rationality [A]. Basel: Birk2houser, 1999.
[4]易余胤,盛昭瀚,肖条军.具溢出效应的有限理性双寡头博弈的动态演化[J].系统工程学报,2004,19(3):244-250.
[5]姚洪兴,徐峰.双寡头有限理性广告竞争博弈模型的复杂性分析[J].系统工程理论与实践,2005,12:32-37.
[6]潘玉荣,贾朝勇.不同理性双寡头博弈模型的复杂性分析[J].复杂系统与复杂性科学,2007,4(2):71-76.
[7]闫安,达庆利.耐用品动态古诺模型的建立及分析[J].系统工程学报,2006,26(2):158-162.
[8]闫安,达庆利,刘心报.耐用品动态Bertrand 模型[J].系统工程,2008,26(5):123-126.
[9]Elber felda W, Wolfst ET ter E. A dynamic model of Bertrand competition with entry [J].International Journal of Industrial Organization, 1999, 17: 513-525.
[10]安同良,杨羽云.易发生价格竞争的产业特征及企业策略[J].经济研究,2002(6).endprint

