筏式养殖区流速垂向分布公式的试验研究

匡翠萍， 李文斌， 单云驰， 江林锋

(1. 同济大学 土木工程学院， 上海 200092； 2. 华东电力设计院有限公司, 上海 200063)

近年来我国海水养殖发展迅速，筏式养殖作为主要浅海养殖方式之一[1]，从20世纪50年代海带筏式养殖开始，至今已经发展成为涉及藻类、贝类、鲍、参、海胆、蟹类等对象不可替代的养殖形式[2].养殖区筏架和网笼的存在对流速影响不应忽视，使得区域水体交换能力下降[3].Gibbs等[4]通过对新西兰贻贝养殖测量发现养殖区流速相比周围减少30%；项福亭等[5]对蓬莱湾扇贝养殖区流速调查发现1975年至1990年15年间养殖中心区最大流速减少近75%，最小流速减少近90%；O′Donncha等[6]使用棒条体模拟双绳延绳式吊样系统，在潮汐水槽模拟发现长绳间流速相比于外部减少25%～30%.如今关于筏式养殖区流速变化的观测和物理试验研究多集中于流速减少比率的情况，而实际对于筏式养殖区的内部、边侧流速垂向分布特征研究仍待发展完善，樊星等[7]对近岸养殖区潮流特征通过现场观测手段进行过研究，对养殖区潮流流速垂直结构特征研究做出探索.本文在矩形断面水槽中进行物理模型试验，将筏式养殖模型布置于水槽之中，设定来流为均匀流，对筏式养殖区的不同点位流速进行测量，利用明渠流流速垂向分布的常用两种形式——对数分布形式和抛物线形式，对流速测速结果进行两种形式拟合，分析确定公式系数，归纳总结得到筏式养殖区不同区域流速垂向分布公式和公式中系数的范围.

1 试验概况

1.1 试验设备

试验在同济大学42 m长波流水槽中进行，水槽断面为矩形，槽宽B=0.8 m，槽深H0=1.2 m.

通过造流装置控制保证来流为均匀流，试验所用物理模型布置在水槽中间10 m范围内以保证试验区上下游一定过渡段长度.流速测量设备为高精度三维流速测量仪ADV(acoustic doppler velocimeter)——挪威Nortek点式流速仪，此设备探头小巧，可以直接连电脑进行实时数据记录，采样体积最小0.085 cm3，可测量流速范围0～4 m·s-1，采样输出频率最高200 Hz，实际采样频率62.5 Hz，即0.016 s读取记录一次流速数据，实际测量时等待流速信号稳定后记录数据1 min，对所得数据作平均计算作为该点的流速值.试验设备如图1所示.

图1 波流水槽和流速测量仪ADV

1.2 试验方案设计

综合实验室实际状况并结合对秦皇岛昌黎县筏式养殖区的现场观测，确定模型长度比尺λl=lp/lm=20(lp,lm分别表示原型和模型的长度)，制作物理试验养殖模型：采用泡沫浮球、塑料圆柱体替代养殖浮球和吊笼，泡沫浮球直径20 mm，塑料吊笼圆柱体长度为100 mm，直径15 mm，浮球与吊笼圆柱体以鱼线进行固定，距离为40 mm.采用柔软抗拉的尼龙鱼线(直径约1 mm对水流影响忽略)替代浮绳、吊绳和锚绳.每列浮绳以10 cm等间距固定10个吊笼模型，后将列模型按一定间距布置于水槽中进行试验.

试验布设和单个模型规格如图2所示，保持来流为均匀流，流速测量点位共7个，分别为M、A、B、C、D、E、F，其中M点位于模型区前2.5 m处，为远离模型区点位，用于测量来流速度；A、B、C点位于水槽布置模型一侧，分别在模型区前0.5 m，模型中央和模型区后0.5 m；D、E、F点位于模型区旁侧，与A、B、C点对称布置.每个测点位垂向测量4个水深位置流速(例如A1、A2、A3、A4)，相应水深分别为0.2H、0.4H、0.6H、0.8H(H为水深).

在重力相似准则下[8]，重力与惯性力的比例系数Fr相等：

(1)

式中:v、g、l分别表示速度、重力加速度和长度;下标l、m分别表示原型和模型.

当重力加速度不变时，可得：

(2)

即

(3)

式中：λv为速度比尺.

秦皇岛昌黎县是我国北方近海养殖大县，近年来养殖规模逐年扩大，参照秦皇岛养殖海域自然条件设定物理模型试验条件[9]：海域潮流流速范围为0～0.6 m·s-1，设定物理模型试验流速范围为0～13 cm·s-1，近海养殖区水深6～12 m，则试验水深范围为0.3～0.6 m.

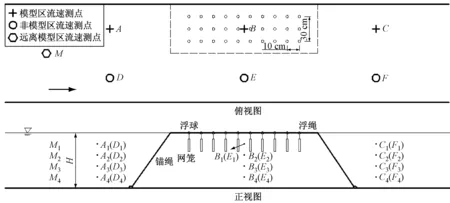
如表1所示设定11组试验，对每组试验的7个测点进行4个垂向相对水深流速测量，图3为3列实物模型及流速测量布置，由于连结两个吊笼之间的尼龙鱼线接触ADV时会对测速产生影响，所以ADV布置在4个吊笼中间，与吊笼和鱼线非接触，以保证流速测量稳定准确.

表1 试验参数设置

1～8组模型列数相同，水深、流速不同，通过对水深、流速进行量纲一化分析得到对应量纲一化流速垂向分布公式；第9、10、11与第3组相比水深、流速相同，模型列数即养殖密度不同，引入与养殖密度相关的公式系数对公式进行修正.

图3 实物模型布置及流速测量

2 试验结果分析

2.1 流速垂向分布公式

明渠水流是一种无压流，目前针对矩形断面明渠流速垂向分布研究，多使用的就是对数分布形式和抛物线形式两种流速分布规律[10-13]：

对数流速垂向分布形式主要是根据Prandtl理论，公式表示为[14]

(4)

式中:H为明渠水深；z为水中任一点到渠道底部的距离；k为Karman常数；umax为垂向最大流速，u为水深z处的流速；u*为摩阻流速.

可以进一步简化得到：

(5)

式中:v为u的垂向平均值；a为与流速切应力相关的系数；b为与流速相关的系数.

明渠的实际流速垂向分布利用抛物线形式进行描述，可表示如下[15]：

(6)

式中：a′、b′、c为待定系数.

2.2 流速拟合及分析

根据式(5)—(6)对不同组别的流速数据使用对数垂向分布形式和抛物线分布形式进行拟合，量纲一化分析描述简洁具有普适性，将测量数据以相对流速u/v为y轴，相对水深z/H为x轴，得到两种形式的拟合曲线和相应的流速垂向分布公式.下面以第1组试验为例，对7个测点进行拟合处理后得到图4，其中圆点为实测值，虚线为拟合的对数函数曲线，实线为拟合的抛物线曲线.

(1) 远离养殖区的M点：

M点为远离筏式养殖区的点位，流速几乎不受养殖区影响，可作为明渠流流速垂向分布的参照点位，整体上符合明渠流流速垂向分布特征，使用两种函数形式拟合情况均较好，拟合度R2均达到0.9以上.而两种曲线拟合结果亦有所差别，对数函数曲线拟合在水面流速达到最大，与实际流速分布略有出入，抛物线曲线在水面附近拟合更好；在明渠近底部流速接近于0，对数函数曲线拟合与明渠近底层流速情况更为接近.

(2) 养殖区一侧A、B、C点：

A点位于养殖区前侧附近，与M点位相比较流速分布总体趋势相近，受养殖区影响较弱.B点为位于养殖区内部点位，因养殖区阻碍作用上层0.8H处u/v下降至0.6左右，对数函数分布曲线在此区域不适用，抛物线曲线拟合精度较好，拟合度R2达到0.84；C点位于养殖区后侧，流速垂向分布形式与B点位相似，但上层0.8H处u/v稍高于B点位，近底层0.2H处u/v低于B点位，而相较于对数函数曲线，抛物线曲线拟合亦较好，R2达0.92.

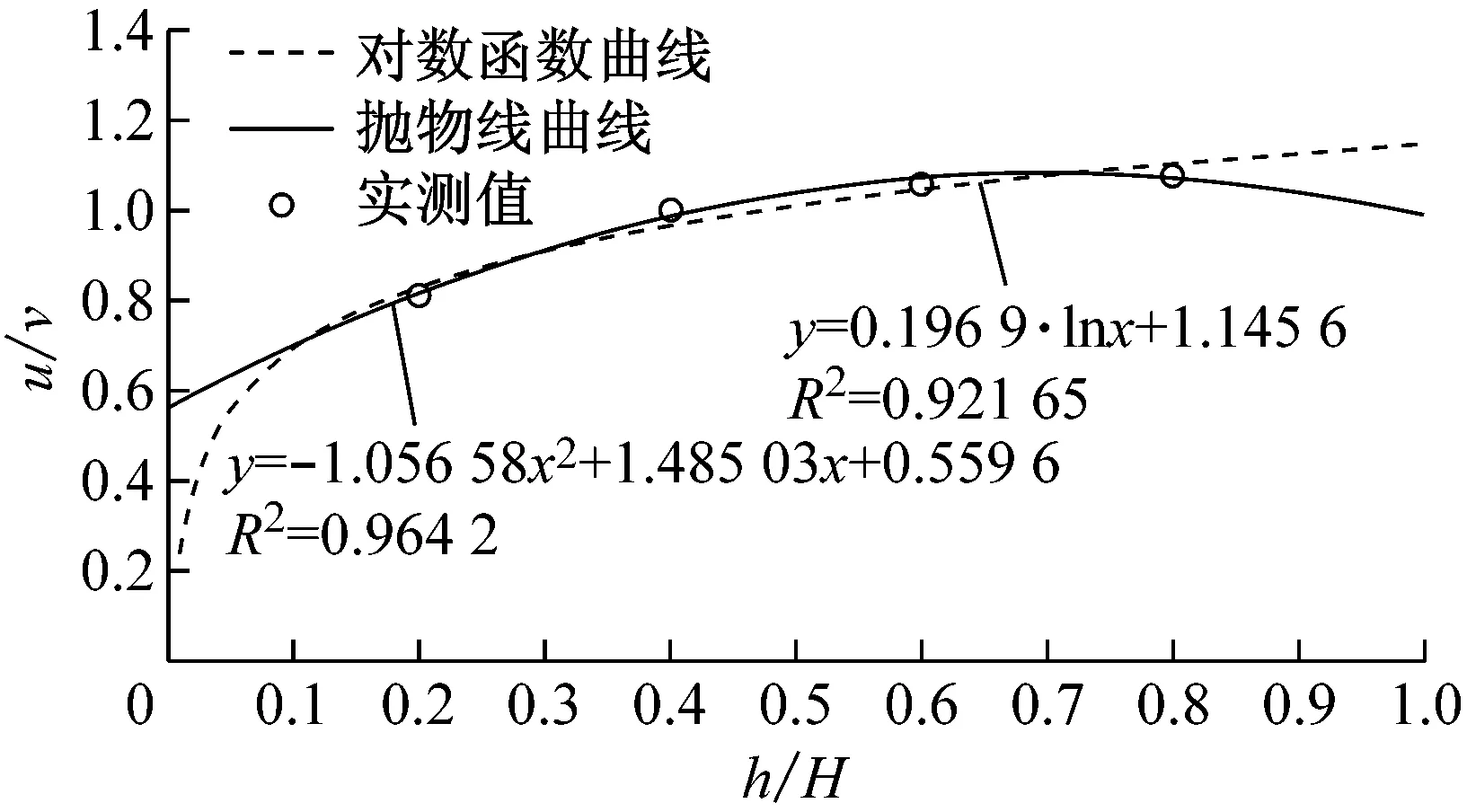
aM点

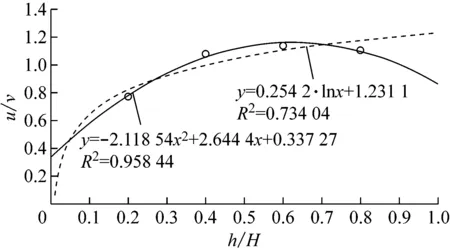
b A点

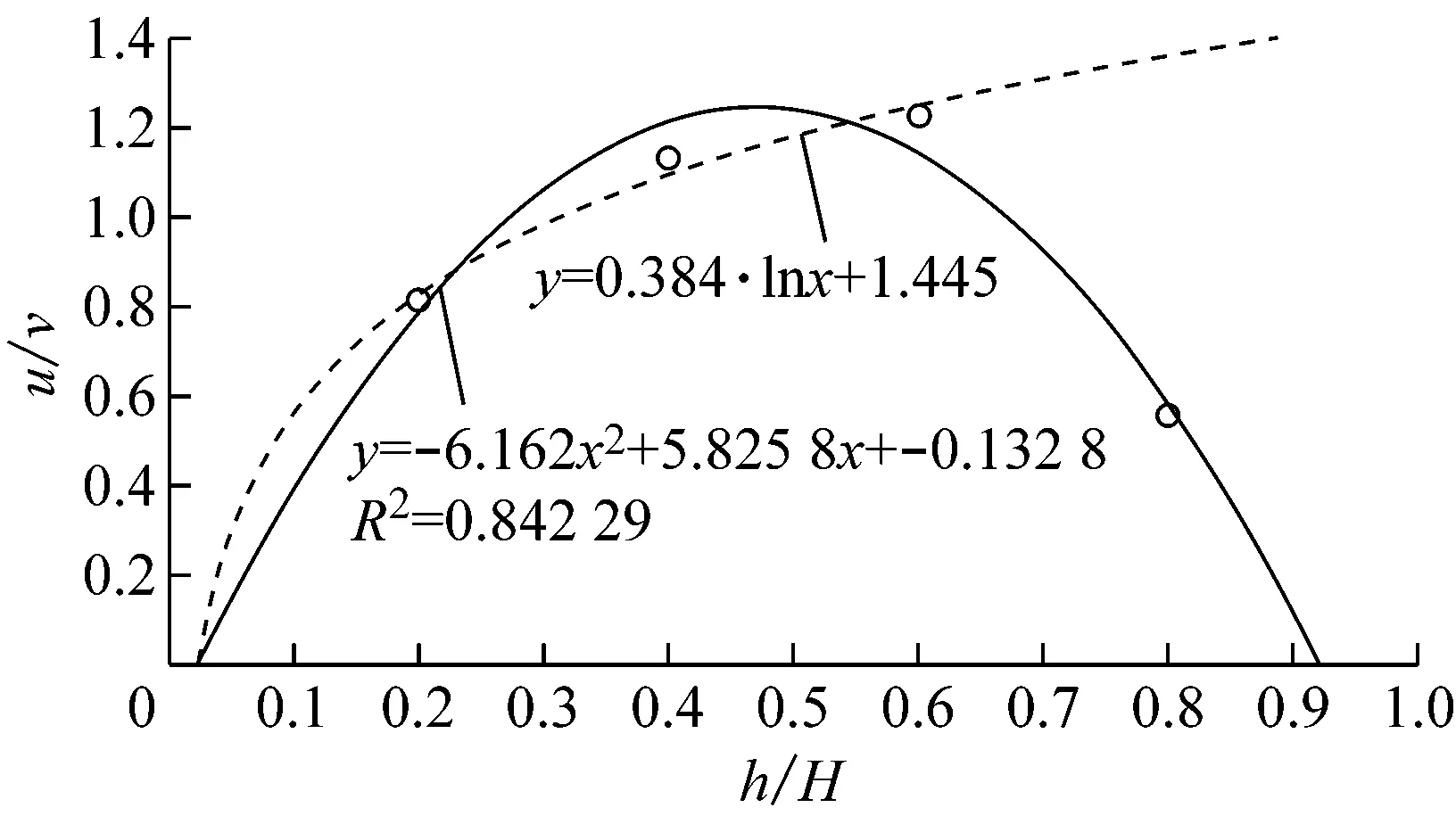
c B点

d C点

e D点

f E点

g F点

图4测点流速垂向分布拟合

Fig.4Curvefittingofvelocitydistributioninverticaldirection

在养殖区一侧，垂向上养殖吊笼影响主要集中在水流上层，即(0.6～1.0)H区域.由于养殖吊笼长度为10 cm、试验水深范围为35～50 cm，因此垂向上养殖吊笼对下部区域(0～0.6H)影响甚微.

(3) 养殖区旁侧D、E、F点：

D、E、F点位于养殖区旁侧，养殖区影响较弱与来流点位M点相比较趋势接近，上层0.8H处流速有所增加，除F点位出现底层流速减小，其余拟合较好，拟合度R2均达到0.9以上.

总体上看：养殖吊笼所在的上层区域流速变化较为明显，下部区域流速变化相对较小，因此分析侧重于近表层区域流速变化分析.B位于养殖区，属于强影响区域，表层流速下降较多，适宜以抛物线曲线进行拟合分析；而位于养殖区后侧的C点位较之B点位影响有所减小，属于中影响区域，适宜以抛物线曲线进行拟合分析.D、E、F点位与A点位于养殖区旁侧与前侧，属于弱影响区域，表层流速增加，以对数函数曲线拟合较为适宜.图5为7个测点对应的7条拟合曲线汇总.

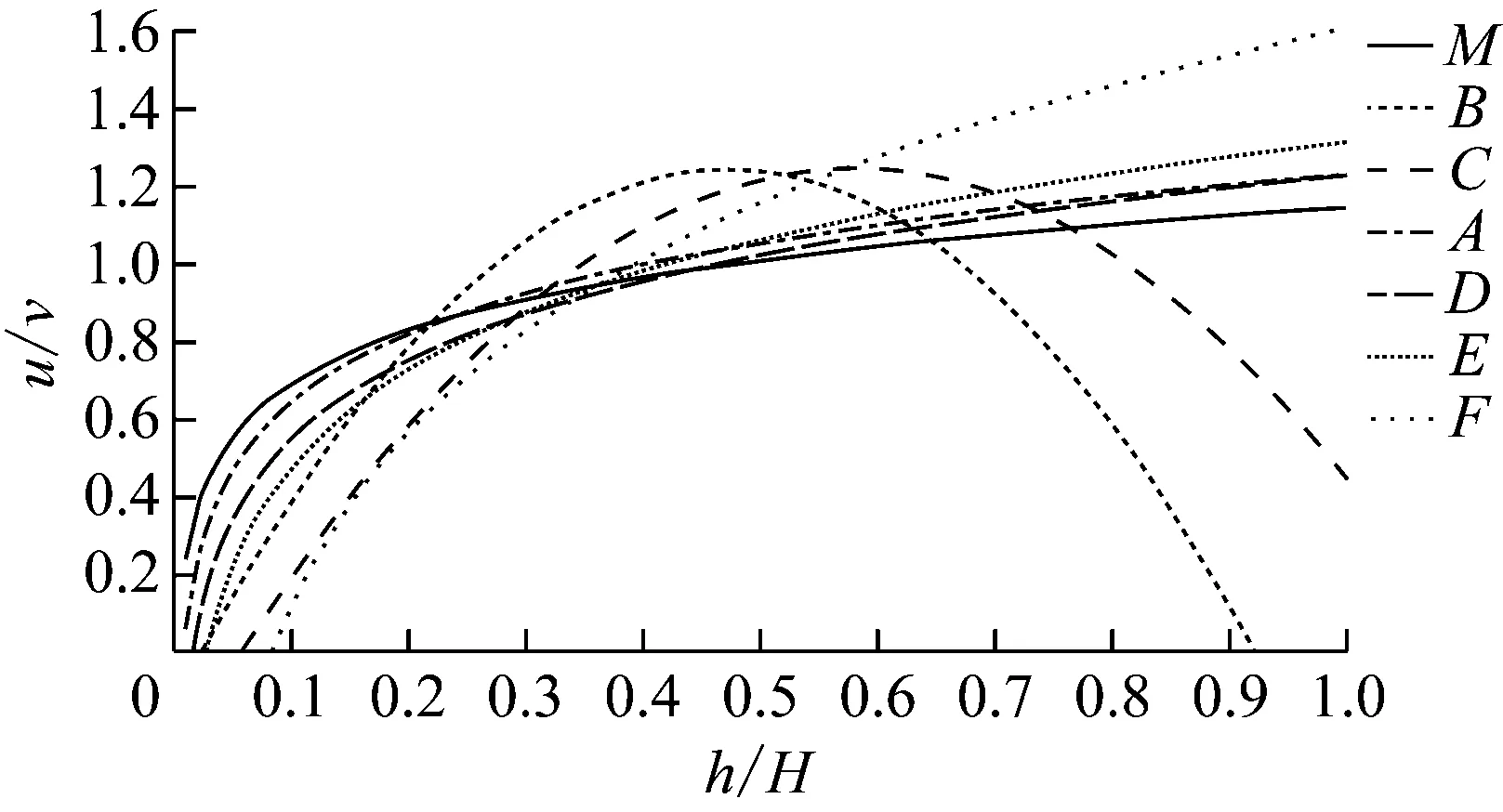
图5 多测点流速垂向分布拟合汇总

2.3 公式系数确定

为了全面反映试验数据样本信息，对公式中系数利用Matlab软件的箱线图进行分析确定，箱线图是用作显示一组数据分散情况资料的统计图.对第1～8组实测数据量纲一化后绘制箱线图，在箱线图的基础上拟合曲线并确定公式系数.

B点与C点为强影响区与中影响区的典型点位，箱线图上的拟合曲线如图6所示，并得到流速垂向分布抛物线函数公式：

(7)

(8)

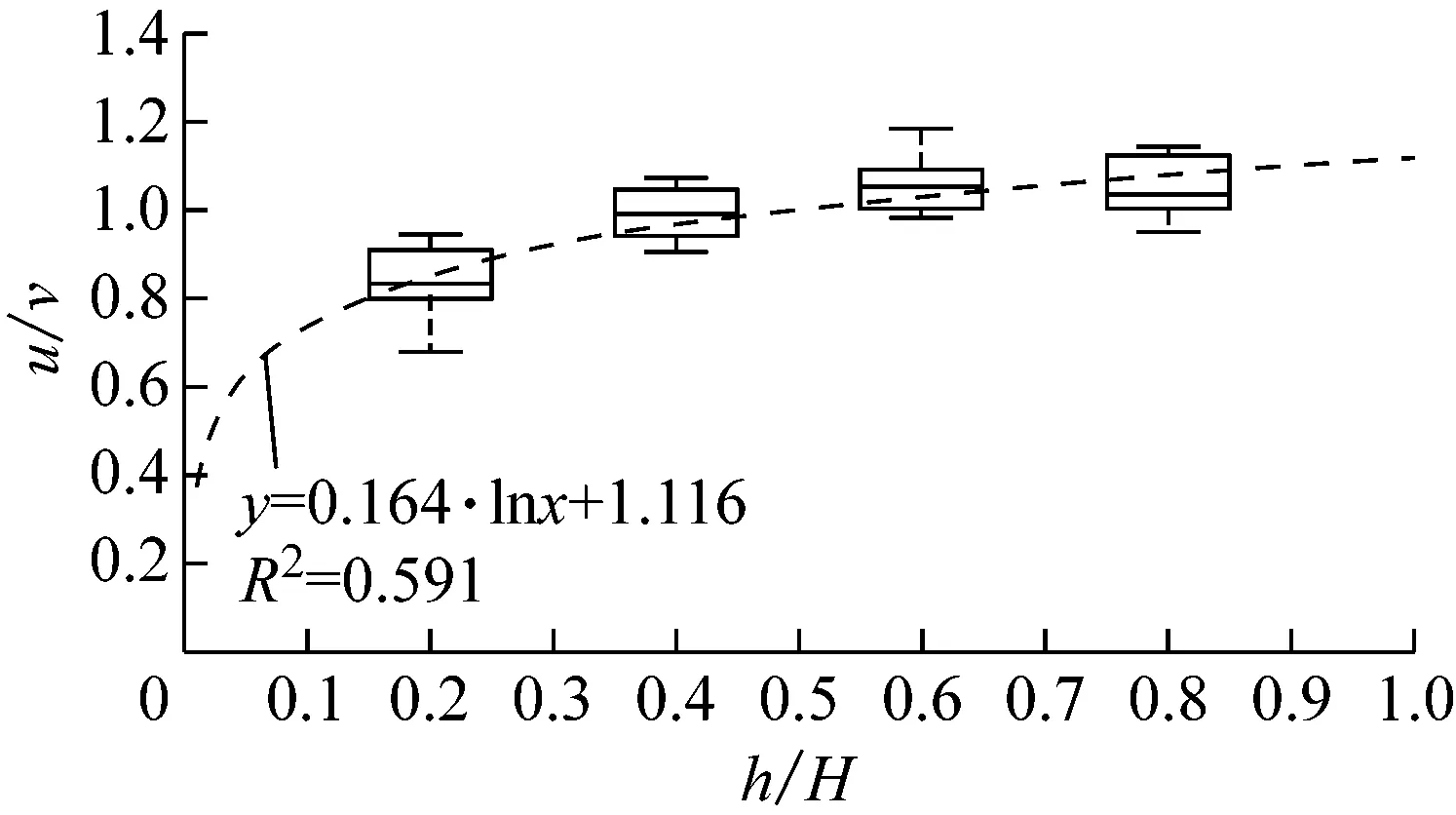
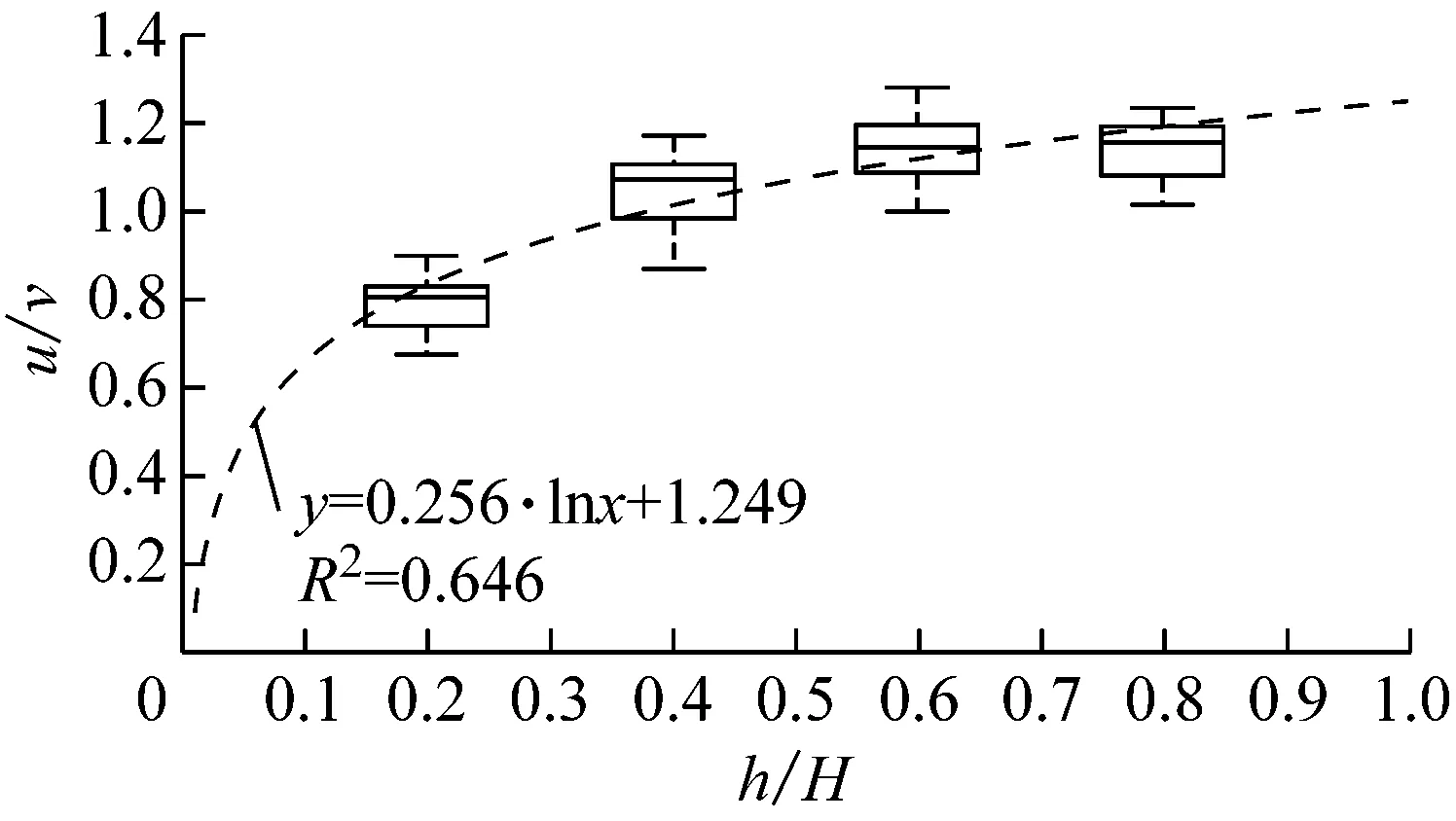
A点与D、E、F点相对于B、C点受养殖区影响较弱，属于弱影响区，箱线图上的拟合曲线如图7所示，综合4点位得到公式中系数的范围，得到弱影响区流速垂向分布对数函数公式：

(9)

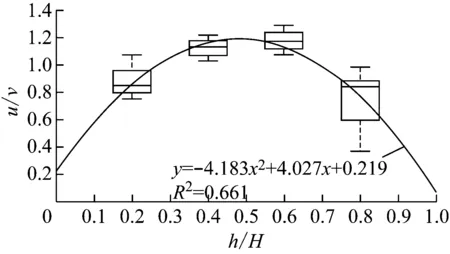
a 强影响区(B点)

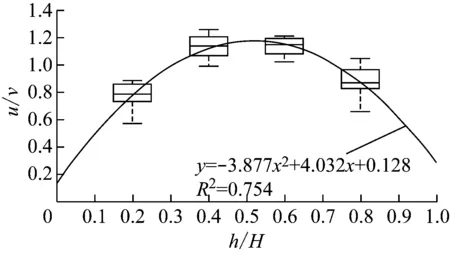
b 中影响区(C点)

2.4 养殖密度的影响与分析

第9、3、10和11组模型列数分别为2、3、4、5，利用同上方法进行拟合，确定这3组不同养殖密度的公式系数如表2、表3.

表2为不同养殖密度下强影响区与中影响区流速垂向分布抛物线公式及其相应的系数，同样的公式分布形式下，强影响区B点位系数a′与b′数值大于中影响区C点；随模型列数2列增加到4列，养殖密度增加后使得公式系数a′与b′数值呈现变大趋势，即拟合曲线的曲率变大，但系数c的数值变化较小.

表2 不同养殖密度下强和中影响区的公式系数

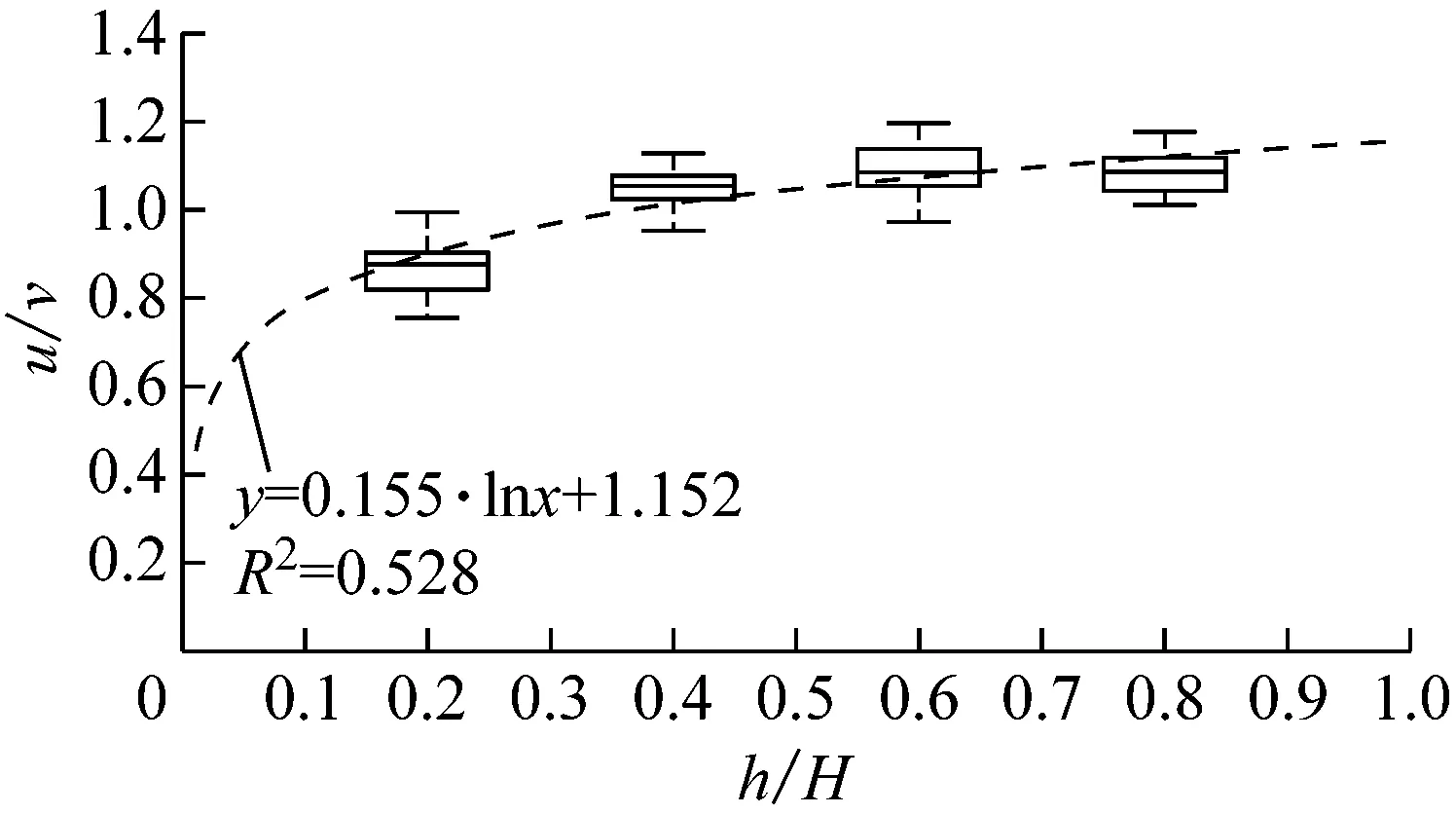
a A点

b D点

c E点

d F点

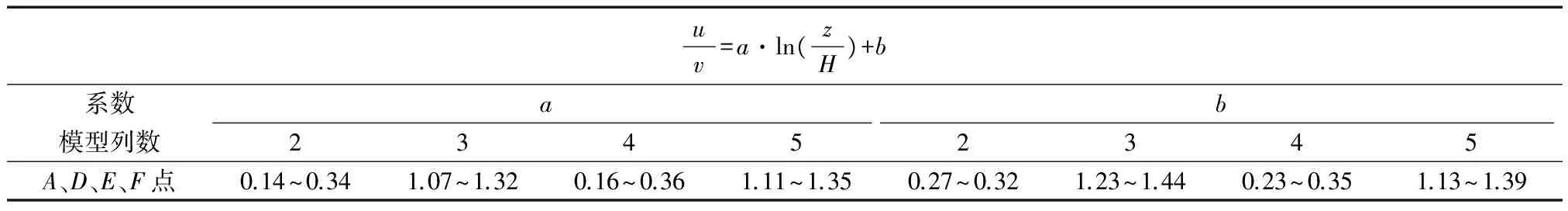
uv=a·ln(zH)+b系数ab模型列数23452345A、D、E、F点0．14～0．341．07～1．320．16～0．361．11～1．350．27～0．321．23～1．440．23～0．351．13～1．39

表3为不同养殖密度下弱影响区与中影响区流速垂向分布对数函数公式及其相应的系数，随模型列数2列增加到4列，养殖密度增加使得公式中系数a和b的上、下限随之增大.

3 结论

本文在矩形水槽中进行了长度比尺为20筏式养殖区的水流实验，采用ADV进行了一系列流速垂向分布测量，利用明渠流理论，以对数函数曲线与抛物线曲线对流速垂向分布进行拟合与分析，按影响程度分为强影响区、中影响区与弱影响区，分别获得强影响区与中影响区流速垂向分布的抛物线型公式以及弱影响区流速垂向分布的对数函数型公式.基于箱线图上的拟合，得到三个区域对应的流速垂向分布公式中的系数以及变化范围.指出了养殖密度的影响特征，即养殖密度增大，抛物线型公式的相应系数增大，对数函数型公式系数上、下限亦增大.

[1] 康伟伟. 河北昌黎海水养殖对海洋生态环境影响研究[D].石家庄：河北师范大学, 2011.

KANG Weiwei. The impact of study of mariculture on marine ecology environment in Changli, Hebei Province[D].Shijiazhuang：Hebei Normal University, 2011.

[2] 丁刚，吴海一，郭萍萍，等. 我国海上筏式养殖模式的演变与发展趋势[J]. 中国渔业经济, 2013, 31(1): 164.

DING Gang, WU Haiyi, GUO Pingping,etal. Evolution and development trend of marine raft cultivation model in China[J]. Chinese Fisheries Economics, 2013, 31(1): 164.

[3] 李铁军，郭远明，徐汉祥，等. 近海筏式养殖造成的水文动力条件变化分析[J]. 浙江海洋学院学报(自然科学版)， 2012, 31(4): 329.

LI Tiejun, GUO Yuanming, XU Hanxiang,etal. Analysing the change of the hydrodynamic condition by suspension aquaculture in shore sea[J]. Journal of Zhejiang Ocean University(Natural Science)， 2012, 31(4): 329.

[4] GIBBS M M, JAMES M R, PICKMERE S E. Hydrodynamics and water column properties at six stations associated with mussel farming in Pelorus Sound[J]. New Zealand Journal of Marine and Freshwater Research， 1991, 25(3): 239.

[5] 项福亭，曲维功，张益额，等. 庙岛海峡以东浅海养殖结构调整的研究[J]. 齐鲁渔业, 1996, 13(2): 1.

XIANG Futing, QU Weigong, ZHANF Yi'e,etal. On aquaculture structure adjustment in shallow sea east to Miaodao Strait[J]. Shandong Fisheries, 1996, 13(2): 1.

[6] O′Donncha F, Hartnett M, Nash S. Physical and numerical investigation of the hydrodynamic implications of aquaculture farms[J]. Aquacultural Engineering, 2013, 52: 14.

[7] 樊星，魏皓，原野，等. 近岸典型养殖海区的潮流垂直结构特征[J]. 中国海洋大学学报(自然科学版), 2009, 39(2): 181.

FAN Xing, WEI Hao, YUAN Ye,etal. The features of vertical structures of tidal current in a typical coastal mariculture area of China[J]. Periodical of Ocean University of China(Natural Science), 2009, 39(2): 181.

[8] 左东启. 模型试验的理论和方法[M]. 北京: 水利电力出版社, 1984.

ZU Dongqi. The theory and method of model experiment[M]. Beijing: Water & Power Press, 1984.

[9] 王中起，韩志远，严冰. 秦皇岛海域水文泥沙特征分析[J]. 水道港口, 2010, 31(4): 247.

WANG Zhongqi, HAN Zhiyuan, YAN Bing. Hydrographic and sediment characteristics in Qinhuangdao sea area[J]. Journal of Waterway and Harbor, 2010, 31(4): 247.

[10] Zhu C, Hao W, Chang X. Vertical velocity distribution in open-channel flow with rigid vegetation[J]. The Scientific World Journal, 2014, 2014(3): 146829.

[11] Ma A, Lu Y, Cao M,etal. Velocity distribution and characteristics in unsteady open-channel flow over rough bed[M]∥Hydraulic Engineering Ⅲ: Proceedings of the 3rd Technical Conference on Hydraulic Engineering (CHE 2014). Hongkong: [s.n.], 2015:15-22.

[12] Pal D, Ghoshal K. Vertical distribution of fluid velocity and suspended sediment in open channel turbulent flow[J]. Fluid Dynamics Research, 2016, 48(3):035501.

[13] 严军，王二平，孙东坡，等. 矩形断面明渠流速分布特性的试验研究[J]. 武汉大学学报(工学版), 2005, 38(5): 57.

YAN Jun, WANG Erping, SUN Dongpo,etal. Experimental study on distribution properties of velocity in rectangular open channel[J]. Engineering Journal of Wuhan University, 2005, 38(5): 57.

[14] 胡春宏，惠遇甲. 明渠挟沙水流运动的力学和统计规律[M]. 北京: 科学出版社, 1995.

HU Chunhong, HUI Yujia. Mechanics and statistical law of sediment llow in open channel[M]. Beijing: Science Press, 1995.

[15] 孙东坡，王二平，董志慧，等. 矩形断面明渠流速分布的研究及应用[J]. 水动力学研究与进展(A辑), 2004, 19(2): 144.

SUN Dongpo, WANG Erping, DONG Zhihui,etal. Discussion and application of velocity profile in open channel with rectangular cross-section[J]. Chinese Journal of Hydrodynamics, 2004, 19(2): 144.