一种应用于谐振式光纤陀螺的数字双相位锁相放大器的设计

张 焱,唐 杰,赵 宁,张 彤1,*

(1.东南大学仪器科学与工程学院,南京 210096;2.东南大学电子科学与工程学院,南京 210096;3.东南大学苏州研究院苏州金属纳米光电技术重点实验室,江苏 苏州 215123)

陀螺是一种用于测量物体角速度和角位移的装置,是惯性导航系统中的关键器件之一[1-3]。谐振式光纤陀螺具有光纤长度短、体积小、检测精度高等特点,使其得到广泛的研究,成为角速度惯性传感领域重要发展方向[4-5]。谐振式光学陀螺的基本原理为光学Sagnac效应[6-7],由于Sagnac效应是一种非常微弱的效应,所以通过Sagnac效应转换得到的电压信号通常是纳伏级别的,具有信号弱、噪声强的特点,如此微弱的信号是无法进行提取的,因此微弱信号检测电路设计为系统电路设计的一个重要的内容。锁相放大器LIA(Lock-in Amplifier)是微弱信号的关键技术之一,它能够改善系统的信噪比,提高检测系统的性能[8-9]。本文设计了一种无需相位调整数字双相位锁相放大器,将微弱的陀螺信号从噪声中检测出来。目前应用于谐振式光纤陀螺的锁相放大器主要有纯模拟锁相放大器、数模混合锁相放大器和数字锁相放大器[10-12]。相比于模拟锁相放大器,数字锁相放大器具有稳定性好、抗干扰能力强以及易于集成等特点,本文所提出的双相位锁相放大器以数字电路方式集成到FPGA上实现。数模混合锁相放大器前端放大、整形、移相和滤波电路主要通过模拟电路实现,后端正交矢量计算通过数字电路实现,结构较为复杂。锁相放大器的性能直接影响到陀螺的输出精度,因此对锁相放大器的研究具有重要意义。

1 谐振式光纤陀螺闭环锁频原理

谐振式光纤陀螺闭环锁频原理如图1所示,激光光束(中心频率为f0)经由相位调制器PM(Phase Modulator)调制后输入光纤谐振腔。其中从谐振腔耦合出的光束,经光电探测器PD(Photodetector)输出转化为电压信号[13-14]。随后利用双相位锁相放大器的相关检测原理对PD探测的电压信号进行同步解调,输出信号为激光器中心频率f0与光纤谐振腔谐振频率的差频信号。将锁相放大器的输出做为PI控制器反馈信号,构建频率伺服回路。伺服反馈将一直进行,直至激光器的中心频率f0锁定到谐振频率上[15]。系统中,相位调制器PM采用正弦波调制信号对光束进行相位调制。

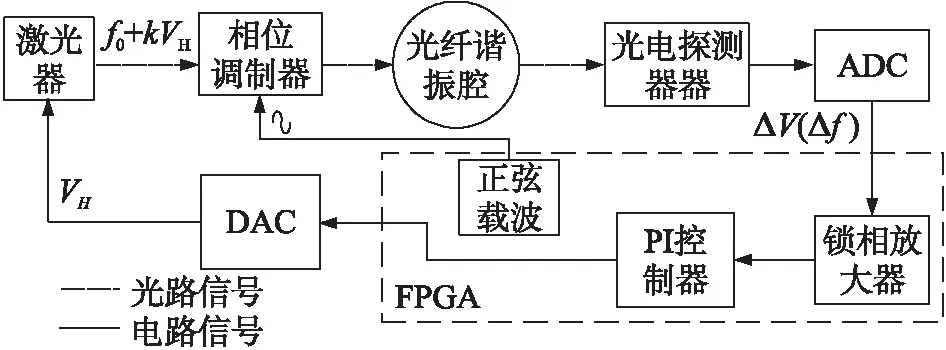
图1 谐振式光纤陀螺闭环锁频原理图

2 双相位锁相放大器的设计

锁相放大器的原理框图如图2所示,主要包括4个部分:信号通道、参考通道、相敏检测器和低通滤波器。

图2 锁相放大器原理框图

设被测信号为

x(t)=Vr·cos(ω0t+θ)

(1)

参考信号输入为

r(t)=Vs·cos(ω0t)

(2)

式中:ω0是待测信号的频率,θ是待测信号与参考信号的相位差。PSD以参考信号为准,对待测信号进行相位检测。PSD输出为:

up(t)=x(t)·r(t)=Vr·cos(ω0t)·Vscos(ω0t+θ)=0.5Vr·Vs·cosθ+0.5·Vr·Vs·cos(2ω0t+θ)

(3)

经过相敏检测后,式(3)变为和频和差频两个分量,再经过低通滤波器,滤除掉和频分量和频带之外的噪声,得到的输出结果为:

u0(t)=0.5Vs·Vrcosθ

(4)

可以看出锁相放大器可以根据待测信号的幅度和初始相位,完成对待测信号的鉴幅作用。当θ等于0时,此时锁相放大器的检测灵敏度最大。通常由于检测信号与参考信号具有相位差,因此需要不断调节参考信号的初始相位。为此我们设计了双相位的锁相放大器,它能够消除初始相位的影响,使得参考信号与待测信号达到相位匹配,且检测灵敏度最大,提高了可操作性。双相位锁相放大器基本结构框图如图3所示。

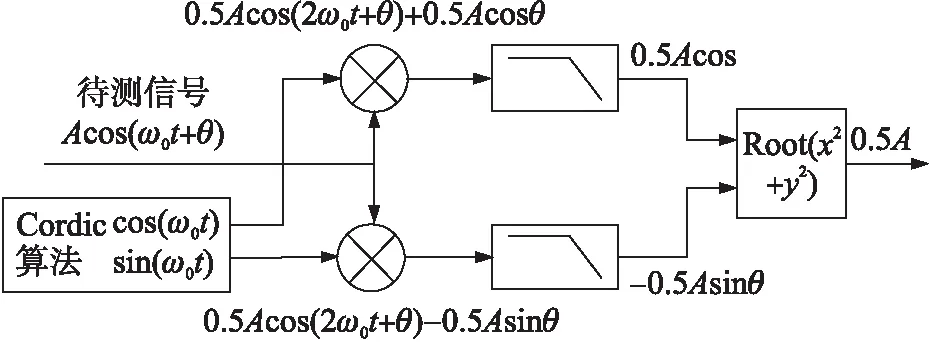
图3 双相位锁相放大器原理图

被测信号分别与CORDIC算法模块输出的正余弦函数相乘[16],各自得到两个差频和和频分量,分别进入低通滤波器输出为两个相位相反的直流分量0.5Acosθ和-0.5Asinθ。将直流分量进行平方相加再开方,最后得到被测信号的幅度信号0.5 A。实现对待测信号最大灵敏度的鉴幅。基于FPGA的双相位锁相放大器设计主要包括CORDIC正余弦信号、加法器、乘法器、开方模块和低通滤波器。其中乘法器和开方器直接调用FPGA内部的集成IP核,设计实现方便简单。

2.1 基于CORDIC算法的正弦信号发生器

正余弦函数的产生一般使用查表法、多项式展开法或者数学逼近法,但这些方法不能满足精度、速度和简单性的要求,在硬件电路上不易实现。CORDIC算法仅用移位和加法运算以产生正弦调制信号,适合FPGA实现。

CORDIC算法以坐标旋转为基础,将旋转角度θ分为若干个连续的小偏转角θi,通过不断迭代的方式摇摆逼近目标旋转角度来实现整个旋转过程。其基本原理如图4所示。

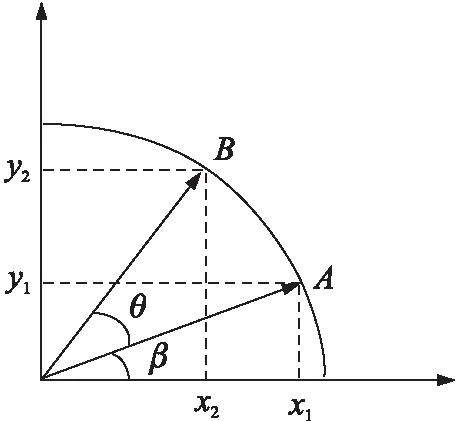
图4 CORDIC算法原理示意图

将XY平面上的点A(x1,y1)旋转θ到点B(x2,y2),新向量的坐标为:

(5)

将上述方程组改成矩阵的形式,可得如下向量:

(6)

CORDIC算法将旋转角度θ分为若干个小部分,每部分旋转一小角度θi。单步旋转定义为:

(7)

式中:提取公因式cosθi,可修改为:

(8)

选取每一次旋转角度θ为正切值为2的指数,除以2的指数可以通过右移操作完成。每次旋转的角度可以表示为:

(9)

所有迭代的累加值最后等于最终所需要的角度θ:

(10)

Si为+1或者-1,根据旋转方向而定,顺时针为-1,逆时针为+1。

余弦值可以通过预先计算而消除掉。

cosθi=cos[arctan(1/2i)]

(11)

将计算过程中所有的余弦值相乘,得到一个增益系数K。

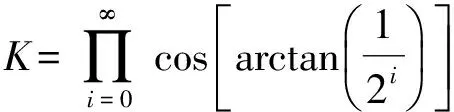
(12)

由于K是常值我们可以忽略它,得到:

(13)

可以看出,CORDIC算法只剩下移位和加减法,非常适合FPGA内部实现。引入变量z,来追踪累加的旋转角度。

zi+1=zi-Siθi

(14)

在旋转模式下,CORDIC算法每次迭代公式为:

(15)

在进行n次迭代后,可以得到:

(16)

通过设置初始值x0=1/k、y0=0和z0=θ,最终得到:

(17)

根据迭代公式,在FPGA内部采用16级流水线实现CORDIC算法,可以提高系统运算速率,获得所需精度的正余弦调制波。根据上述原理,在FPGA内部编好相关代码后,通过Modelsim仿真,得到的输出仿真结果如图5所示。

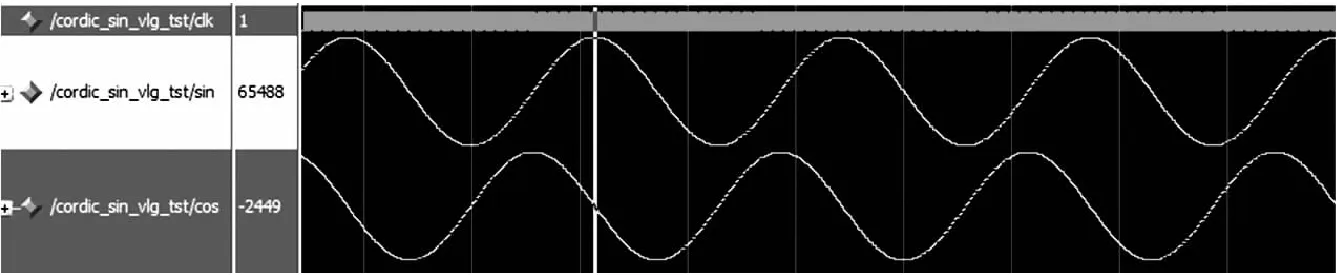
图5 CORDIC算法仿真图

由图5可以看出,通过仿真成功得到了正弦与余弦曲线。

根据CORDIC算法,设置频率控制字和相位控制字之后,在FPGA内部就能够产生相应参数的正余弦波形。用频谱分析仪对输出波形进行频谱分析,得到的结果如图6所示。从图6可以看出CORDIC模块产生了800 kHz的正弦波,噪声基底在-61.8 dBm以下,即信噪比达到了71.4 dB,得到的优良的正弦波信号,符合设计指标。

图6 正弦信号频谱分析图

2.2 低通滤波器的设计

在锁相解调模块中,相敏检测器的输出信号为二倍频交流分量和直流分量两部分,低通滤波器滤除掉前者和系统中频带外噪声,提高系统的信噪比,得到反映陀螺转动的直流信号。因此低通滤波器的设计也是锁相解调模块的重要部分。

低通滤波器设计以一阶无限脉冲响应IIR(Infinite Impulse Response)滤波器为基础。图7为低通滤波器的基本原理图。

图7 一阶低通滤波器原理图

根据图7建立起的数字滤波环路的传递函数为:

(18)

式中:F为系统的时钟频率,系统的截止频率为,通过设置K和F,可以得到符合设计指标的低通滤波器。根据式(18),设计截止频率为1 kHz的低通滤波器,得到的幅频响应曲线如图8所示。其中红色为仿真曲线,黑色点为实验测试结果,可以看出实验结果与理论分析基本吻合。

图8 IIR滤波器幅频响应曲线

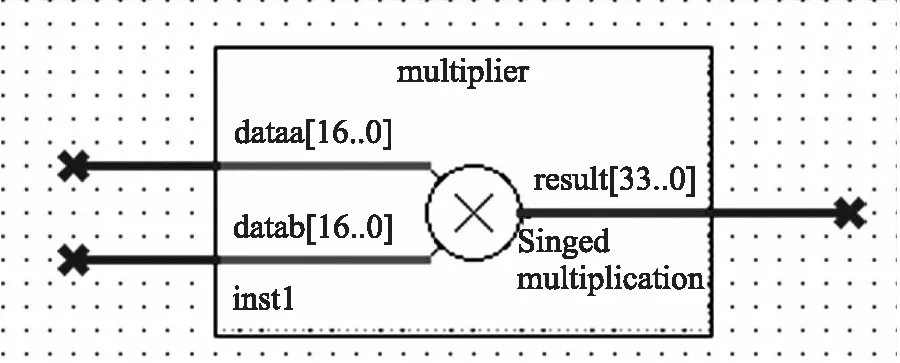
图9 乘法器顶层原理图

2.3 基于IP核的乘法器和开方器的设计

Altera在其开发集成环境中提供了IP核实例化和调用功能。本系统设计中采用了大量的IP核,包括乘法器和开方器。这些IP核大大的简化了设计过程,缩短了开发周期。

如图9和图10分别为带符号乘法器的顶层原理图和Modelsim仿真图。可以看出乘法器输出无时钟延迟,适合检测系统高速设计的要求。

图10 带符号乘法器仿真图

同样对调用的IP核开方器在Modelsim上进行仿真,如图11和图12为开方模块顶层原理图和Modelsim仿真图。

图11 开方器顶层原理图

图12 开方器仿真图

通过仿真结果可以看出调用的IP核乘法器和开方器的输出符合逻辑功能设计,无系统延时,可以直接调用。

3 实验与讨论

对设计的锁相放大器进行线性度测试,用信号发生器产生正弦波信号,经过ADC采集后送入FPGA内部,通过双相位锁定放大器探测,输出为正弦波信号的幅度信息。输入信号的幅度从50 mV增加到4 V,在Signaltap II内对锁相放大器的输出进行采样保存,最后得到的锁相放大器的线性度测试曲线如图13所示。可以看出解调输出基本上成一条直线,线性度良好。将小信号解调输出放大,可以看到小信号解调输出也基本成一条直线,线性度依然良好。

图13 双相位锁定放大器线性度测试图

如图1所示搭建单路光纤谐振腔信号调制解调测试系统。用锯齿波信号对激光器进行扫频,可以测得光纤谐振腔的谐振谱线如图14(a)所示。通过该谱线测得光纤谐振腔的自由谱宽FSR为112.5 MHz,半高全宽FMHW为2.7 MHz,清晰度为41.7。在FPGA内部采用CORDIC算法产生频率为800 kHz,峰峰值为4Vpp的正弦信号给相位调制器对光波信号进行调制,并将光电探测器输出的模拟信号通过DAC转换为数字信号,送入在FPGA内部构建的双相位锁定放大器。锁相放大器的参考信号为CORDIC算法产生的同频的正弦波信号。通过双相位锁相放大器的解调得到的输出曲线如图14(b)所示,右上角局部放大图中黑色曲线为锁相输出线性工作区间,红色曲线为拟合曲线。通过拟合得到锁相放大器输出线性区间的线性度为0.999 77。结果表明,得到的解调曲线在谐振频率处具有较高的线性度,这使得陀螺将具有较大的动态范围和角速度测量精度。

图14 光纤谐振腔扫频曲线

4 结论

本文介绍了谐振式光纤陀螺锁频系统的原理,设计了一种无需相位调整的应用于谐振式光纤陀螺的双相位锁相放大器。与传统的模拟锁相放大器相比,该锁相放大器采用数字电路实现,并集成到单片FPGA上,具有抗干扰能力强,易于调节等特点。通过该锁相放大器解调,得到了高线性度的解调曲线。该线性区间为谐振式光纤陀螺的工作区间,因此可以获得高线性度的陀螺输出转动信号,表明该锁相放大器具有良好的性能。

[1] 郭秀中. 惯性系统陀螺仪理论[M]. 国防工业出版社,1996.

[2] Barbour N,Schmidt G. Inertial Sensor Technology Trends[J]. Sensors Journal IEEE,2001,1(4):332-339.

[3] Qian G,Tang J,Zhang X Y,et al. Low-Loss Polymer-Based Ring Resonator for Resonant Integrated Optical Gyroscopes[J]. Journal of Nanomaterials,2014,2014(3):119.

[4] Zhang T,Qian G,Wang Y Y,et al. Integrated Optical Gyroscope Using Active Long-Range Surface Plasmon-Polariton Waveguide Resonator[J]. Scientific Reports,2014,4(1):3855.

[5] Qian G,Fu X C,Zhang L J,et al. Hybrid Fiber Resonator Employing LRSPP Waveguide Coupler for Gyroscope[J]. Scientific Reports,2017,7:41146.

[6] Lee B. Review of the Present Status of Optical Fiber Sensors[J]. Optical Fiber Technology,2003,9(2):57-79.

[7] Culshaw B. The Optical Fibre Sagnac Interferometer:An Overview of its Principles and Applications[J]. Measurement Science and Technology,2005,17(1):R1.

[8] 刘顺,李晓,王志斌,等. 基于弹光调制旋光测量的信号解调系统[J]. 传感技术学报,2016,29(7):1021-1025.

[9] 陈浩,闫树斌,郑永秋,等. 应用于谐振式光纤陀螺的双相位锁相放大器的设计[J]. 仪表技术与传感器,2014(11):93-95.

[10] 陈浩. 谐振式光学陀螺闭环锁频关键技术[D]. 太原:中北大学,2015.

[11] 樊天麒,刘岩,雷冲,等. 基于V/I转换电路与锁相放大器的磁阻抗测量系统简[J]. 传感技术学报,2016,29(10):1602-1605.

[12] 杨俊义. 基于FPGA的数字锁相放大器研究[D]. 浙江大学,2012.

[13] Hong J B,Yeo Y B,Lee B W,et al. Phase Sensitive Detection for Mode-Locked Fiber Laser Gyroscope[J]. IEEE Photonics Technology Letters,1999,11(8):1030-1032.

[14] Zhi Y,Feng L,Lei M,et al. Low-Delay,High-Bandwidth Frequency-Locking Loop of Resonator Integrated Optic Gyro with Triangular Phase Modulation.[J]. Applied Optics,2013,52(33):8024-31.

[15] 闫树斌,陈浩,郑永秋,等. 谐振式光纤陀螺闭环锁频系统[J]. 红外与激光工程,2014,43(12):4061-4065.

[16] Hu Y H. CORDIC-Based VLSI Architectures for Digital Signal Processing[J]. IEEE Signal Processing Magazine,1992,9(3):16-35.