基于简易风洞的薄翼模型升力测量实验
何建勋 唐 芳 熊 畅 王志超
(1北京航空航天大学能源与动力工程学院,北京 100191;2北京航空航天大学物理科学与核能工程学院,北京 100191;3北京航空航天大学数学与系统科学学院,北京 100191)
当前以飞机为主的航空飞行器扮演了越来越重要的角色,对航空飞行器工作原理的普及教育也愈加必要。简单而言,大部分航空飞行能够离开地面飞上天空,是因为通过对机翼翼型的气动设计,翼型上下表面附近的空气产生了压力差。而该压力差的综合效果除产生升力外,还有沿来流反方向的分量,称为翼型阻力,需要通过发动机提供推力与之平衡。在翼型设计中,需要尽量提高翼型升力、降低阻力。
翼型的升力可通过风洞实验测得,大量的实验结果表明,翼型的升力与来流速度、流体密度以及翼型形状均有关。为研究翼型参数对升力的影响,消除流体的因素,可以引入升力系数的概念。升力系数是翼型的重要参数,通过实验来研究不同形状翼型的升力系数,及不同来流速度时升力系数与迎角的关系,对航空飞行器设计以及叶轮机械的设计等都有着重要意义。
对于无粘不可压完全气体翼型扰流和薄翼模型,可以通过对流场进行小扰动线性近似而获得升力的解析解[1]。然而,由于其过程相对抽象,无专业知识的本科低年级学生很难理解。而如果能借助实验对薄翼型升力理论进行验证,会加深学生对模型和理论的理解[2],提升薄翼型理论的教学效果。
实验选取展宽b=143mm、弦长l=224.5mm、最大厚度a=33.5mm的翼型,满足薄翼型理论对翼型的要求。设计风速可调的简易风洞,用空速管测量流速,利用不影响流体分布的弹簧测力装置测量升力。改变迎角,研究不同流速下升力系数与迎角的关系。通过对实验数据的分析可知,虽然简易风洞存在不满足理论模型的因素,但是并不影响参数变化的趋势,得出的结论和薄翼型理论结果基本吻合,该实验装置也可用于其他自制模型的升力测试和研究。
1 薄翼型理论相关知识
由空气动力学的相关知识,翼型的升力系数可以定义如下[3]
(1)
其中,Y为升力;CY为升力系数;ρ为流体的密度;v为来流速度;l和b分别为翼型的弦长和展宽。升力系数是在特定流动下翼型的参数,与流体的种类和流速无关。
由空气动力学给出的薄翼型理论,对于不可压无粘流体的翼型扰流,在翼型的厚度、弯度和迎角都不大时,绕流场可以认为是一个小扰动的势流场,可以进行线性化近似[1]。在这种假设下,翼型升力系数由中弧线、厚度以及迎角唯一确定。对于确定的翼型,中弧线方程和厚度已经确定,迎角和升力系数存在一一对应关系。
于是薄翼型理论下的升力系数为[3]
其中,α为来流相对于翼型前缘的迎角;yf=y(x)为翼型中弧线方程;l为弦长。通过式(2)~式(5)就可以计算出升力系数与迎角的一一对应关系。
2 简易风洞实验装置和测量过程
实验用简易风洞结构如图1所示,鼓风机从外部吸入空气,经收缩段加速后进入试验段,提供不可压缩的低速气流,试验段截面为矩形,宽度B=510mm,高度H=510mm。在试验段放入翼型,空气流经翼型表面使其产生升力,可在此进行实验和测量,实验后气流通过扩压段降速排出。
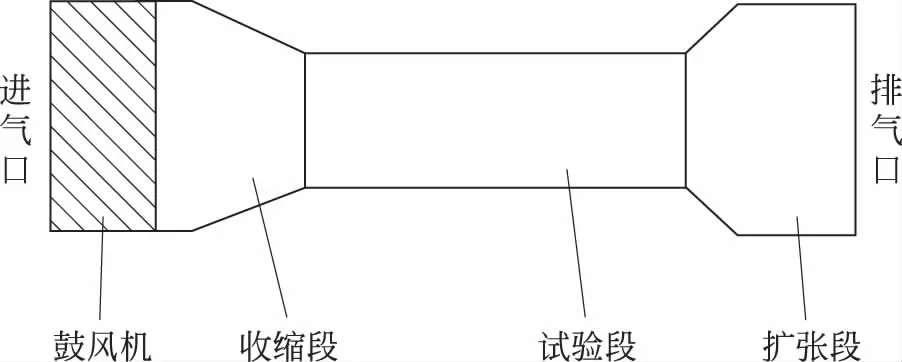
图1 简易风洞结构简图
一般的风洞实验升力是利用风洞天平直接测量或通过打孔测翼型表面压强分布而获得。对于小型风洞,风洞天平的引入会严重改变翼型周围的气流分布。而打孔测翼型表面压强分布在设备结构和数据处理上会比较复杂。本实验所用的测力装置和测迎角装置分别如图2(a)、图2(b)所示。为了实现升力的测量,在风洞的顶部开一窄缝,实验翼型的顶部安装两个铰接细杆,翼型受升力作用时两铰接杆上移,推动弹簧使压缩带动指针示值发生变化,指针示值即可表示升力的大小。为保证升力示值的准确,用精度为0.1g的电子天平对弹簧升力计进行了校准。同时通过调节两铰接杆的上下位置可以固定和改变翼型的迎角,如图2(b)所示迎角示值可以由弹簧秤座上读数读出为8°。
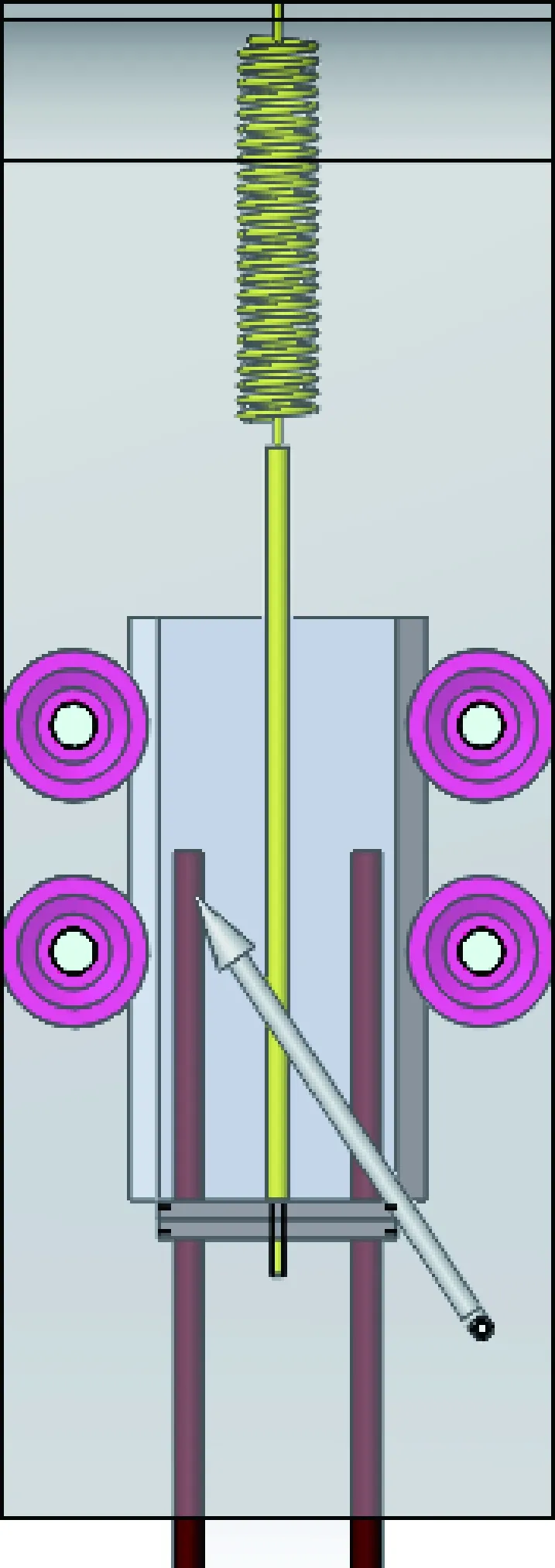
图2(a) 测力装置
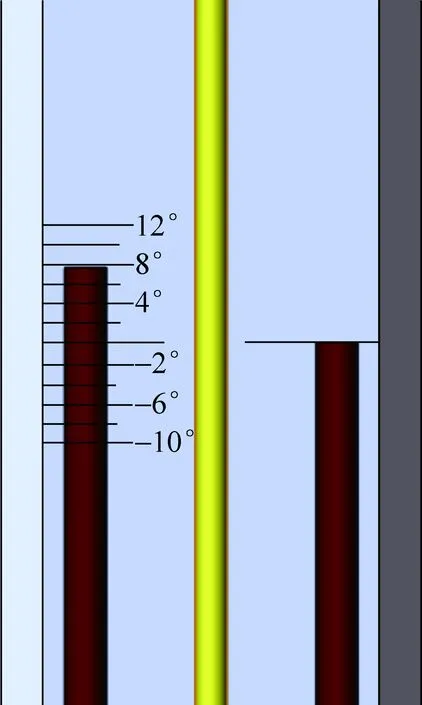
图2(b) 测迎角装置
2.1 翼型中弧线方程的建立
本实验所用翼型如图3(a)所示,在剖面上建立平面直角坐标系,通过测量得到翼型上下表面对应位置点的坐标,取坐标平均值得到中弧线上一些点的坐标(x,y),由多项式拟合得到中弧线方程。中弧线的拟合结果如图3(b),拟合方程为
(6)
其中,l为翼型的弦长;a为翼型中弧线的最大高度。

图3(a) 实验翼型图片
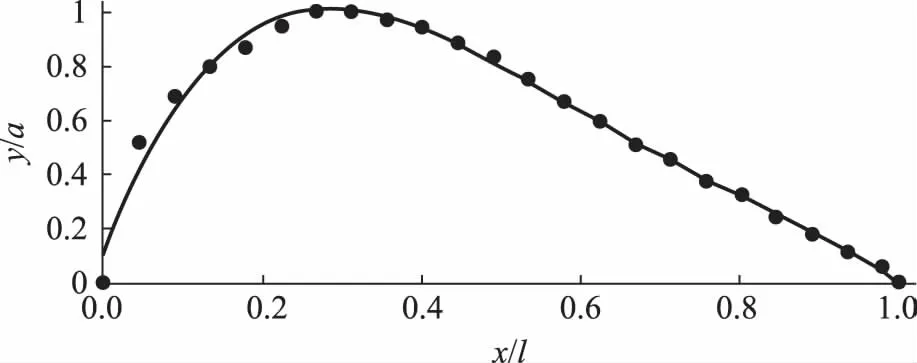
图3(b) 翼型中弧线拟合结果
取定一系列翼型迎角α,将式(6)代入式(3)、式(4),并结合式(2)和式(5)可以得到不同迎角对应的升力系数理论值CY0。
2.2 升力系数的实验测量
借助简易风洞,测量翼型升力、迎角和空气流速。如前所述,翼型的升力由测力装置直接读出,迎角由弹簧秤座上的迎角刻度显示。来流速度的测量借助于空速管[4],由不可压流体的伯努利方程得来流速度的计算公式
(7)
其中,p*为流体总压;p为流体静压;Δp为流体的总静压差;v为来流流速;ρ为流体密度。通过测量总静压差可以求得来流流速。
由式(2)~式(5)可以计算出不同迎角下的升力系数,实现简易风洞对薄翼型理论的研究。
3 结果与讨论
下面分别从实验结果的重复性、线性度和空气流速的影响3个方面讨论,以论证简易风洞研究薄翼型理论的可行性。
3.1 结果的线性度和重复性

图4 升力系数测量值与迎角的关系。CY1、CY2、CY3为相同条件下重复测量的3组升力系数结果
多次重复测量不同迎角对应的升力系数如图4所示。由图4可知,升力系数与迎角的线性相关性较好,满足薄翼型理论中“升力系数和迎角呈线性关系”的结论。而且相同实验条件下多次重复测量不同迎角下的升力系数,如图4所示3组数据的重复性也很好,且迎角越小重复性越佳。由此说明即使简易风洞中的流动呈现强烈的非定常性,粘性的影响也不容忽略,实验的重复性同样可以得到满足。
3.2 流速对结果的影响及与理论值的比较
由薄翼型理论可知,无粘定常流动下升力系数是翼型的参数,理论上与流体的种类及流速无关。通过调节风机的档位改变来流速度,在不同来流速度下分别测量升力系数与迎角的关系。实验结果做线性拟合如图5所示。
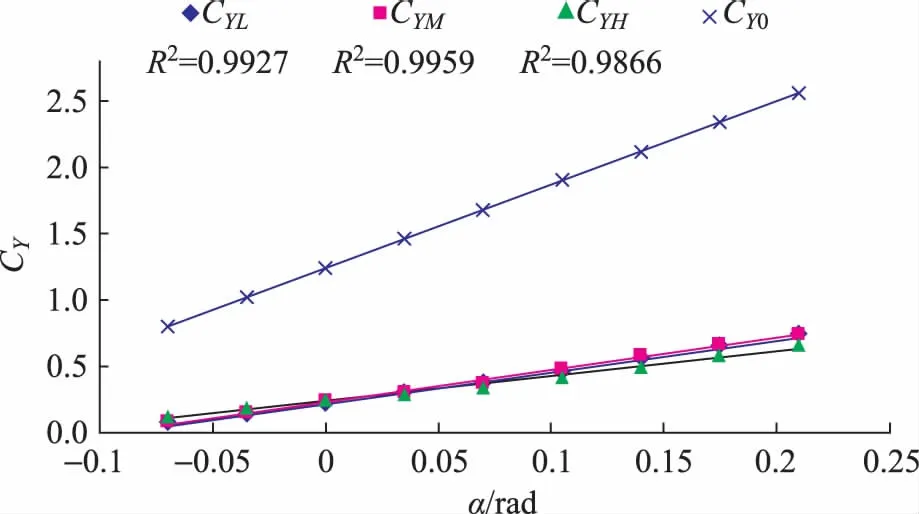
图5 不同来流速度下升力系数的测量结果
图5中CY0是升力系数理论结果,CYL、CYM、CYH分别为低、中、高流速下测量的翼型升力系数,来流速度大小分别对应8m/s、10m/s、12m/s。因来流速度受出口反压影响,所以改变翼型迎角的过程中同时改变了出口截面积,流速会发生变化,所以来流速度很难在一次实验中完全固定,低、中、高流速值仅仅是多次测量的平均结果。
由图5可得:来流速度对升力系数影响不大,且线性拟合结果较好,从而在实验中证明了升力系数是翼型的固有参数,与来流速度无关,符合薄翼型升力系数的相关理论。
4 误差评定和分析
由图5可以看出,实验值和理论值之间存在较大误差。下面分别从升力测量装置的系统误差和理论模型差异两方面进行分析。
4.1 升力测量装置导致的系统误差
如上文所述弹簧测力装置的读数已用电子天平进行校定,得到用天平校准的升力值F0与升力计读数F的关系,结果如图6所示。
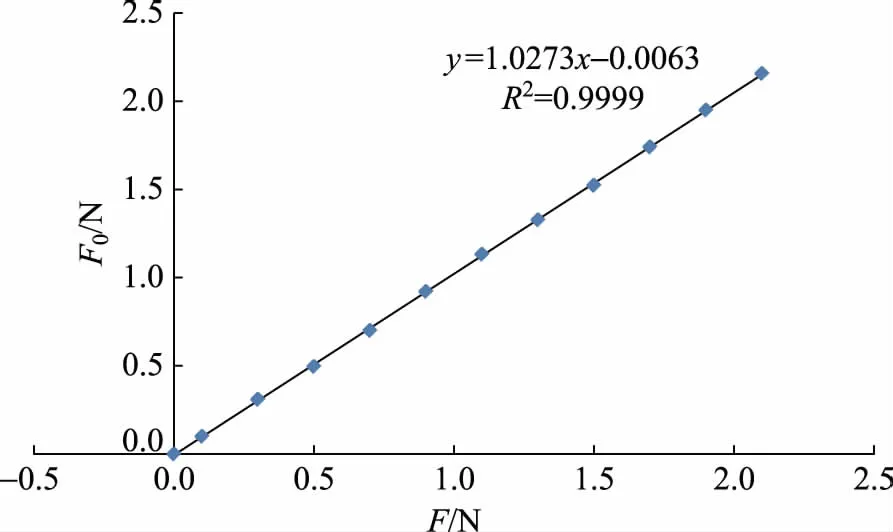
图6 用电子天平对升力计校准的结果
对F0和F的测量结果做线性拟合,其结果为
F0=1.0273F-0.0065
(8)
由式(8)可得,校准所得的升力值F0和升力计读数F虽存在一定偏差,但偏差程度不大,不足以导致升力系数测量值与理论值之间的较大误差。
4.2 实验模型和理论模型的差异导致误差
薄翼型理论仅适用于流体受到的扰动可以进行线性化处理,忽略了湍流脉动的掺混损失,而简易风洞由于自身结构简单,湍流度较大,与理论模型存在较大的差异,这也是导致实验误差较大的主要原因。若取空气密度ρ=1.2kg/m3,特征速度v=10m/s,粘性系数μ=18.1×10-6kg/(m·s),特征长度取风洞的特征尺寸b′=143mm,计算基于风洞尺寸给出的雷诺数:
(9)
简易风洞可近似为管流,管流的湍流度T可通过雷诺数进行近似估计:
(10)
计算所得简易风洞湍流度在5%左右,而科研用风洞的湍流度一般在1%以内[5]。湍流度过高使得流体在风洞中变得不稳定,在翼型的扰动下会造成气流长距离的湍流脉动,湍流脉动对宏观流动的作用效果不可忽略[6],导致测量误差较大。此外,风机鼓出的空气很难保证直匀流动,且在翼型的后半段存在边界层的分离[3],风洞内部流动存在较大的三维性,掺混造成的损失和翼型后缘处的分离损失亦不可忽视。上述原因导致了简易风洞中的实际翼型绕流偏离小扰动线性化理论的成立条件,使得实验测量值小于理论值。
5 结语
利用简易风洞和弹簧测力装置设计了薄翼模型升力系数测量实验。实验测得的升力系数与迎角满足线性关系,符合薄翼型理论结果。改变来流速度,数据的重复性较好,从而验证了升力系数与来流速度无关的结论。由于简易风洞并不能完全满足薄翼型理论要求,会造成一些不可避免的误差,但数据的总体趋势和线性关系与理论是相符的。该简易风洞实验可用于教学,有助于学生理解抽象的空气动力学知识,提高教学效果;学生也可自制翼型进一步研究不同翼型与升力系数的关系。
[1] 单鹏. 多维气体动力学基础[M]. 北京:北京航空航天大学出版社,2008.
[2] 陆瑞征, 黄丽菊. 读《定性与半定量物理学》谈工科物理教学改革[J]. 大学物理,1998, 17(4):37-39. LU Ruizheng, HUANG Liju.Teaching reform of engineering physics based on reading “Qualitative and Semi-quantitative Physics”[J]. College Physics, 1998, 17(4): 37-39. (in
Chinese)
[3] 钱翼稷. 空气动力学[M]. 北京:北京航空航天大学出版社, 2004.
[4] 刘扬正, 钱仰德. 测定不同形状物体空气阻力系数的实验[J]. 大学物理,2017, 36(3). LIU Yangzheng, QIAN Yangde. The experiment of measurement the air drag coefficient of different shape objects[J]. College Physics, 2017, 36(3). (in Chinese)
[5] 何克敏, 屠兴. 低湍流度风洞及其设计[J]. 流体力学实验与测量, 1988(2):11-18. HE Kemin, TU Xing. Design of low turbulence wind tunnel[J]. Experiments and Measurements in Fluid Mechanics, 1988(2): 11-18. (in Chinese)
[6] 王洪伟. 我所理解的流体力学[M]. 北京:国防工业出版社, 2014.

