不确定分析法快速估算资源量实现步骤及关键

吕 睿

(中国石化集团 国际石油勘探开发有限公司，北京 100083)

引 言

油气新项目评价及勘探开发过程中，圈闭资源量估算是一项十分重要的工作，是新项目决策的前提，是圈闭优选排队及勘探部署的重要依据之一。圈闭资源量估算多用于油气勘探初期，无法得到油井的生产动态趋势，多采用静态容积法。

容积法可分为传统容积法和不确定性容积法两类，传统容积法是取每个参数的最佳估算值，直接计算得到一个最佳的资源量估算值。对勘探新区、地质条件复杂等情况，最佳储量估算值不易得到且可靠度差，此时采用不确定性容积法，选择计算参数概率分布模型及变量合理赋值范围，通过蒙氏模拟随机抽取各参数的概率分布值进行成千上万次迭代(模拟次数)后进行计算，可以得到资源量估算范围即不同概率下的油气资源量规模。此方法被国际上大油公司和机构所采用，如壳牌、美孚、美国地质勘探局( USGS) 等[1]。其较之前者更为客观，认识更为全面。

1 应用概率估算公式

不确定分析法估算圈闭资源量采用的仍是容积法基本公式，常用公式为[2]

N=Ao·h·φ·So·ρo/Boi。

式中：N为圈闭资源量，104t；Ao为圈闭有效含油面积，km2；h为平均油气层有效厚度，m；φ为储层有效孔隙度；So为含油饱和度(So=1-Sw)，Sw为含水饱和度,无因次量；ρo为油常温常压下密度；Boi为油体积系数,无因次量。

计算参数一般不是定值，是具有一定分布形式及取值范围的随机变量，而资源量计算结果是一个提供不同概率下的范围值。

2 主要计算参数的确定方法及概率分布模型选择赋值

2.1 概率分布模型及赋值方式

资源量计算公式中参数的分布形式可以用概率分布模型来表示，其描述了一定范围值发生的频率，可确定某数值在其范围内发生的概率大小。常用的概率分布模型有正态分布、对数正态分布、Beta分布、三角分布、均匀分布等， 可用概率密度函数曲线和逆累计概率函数(超越概率函数)两种曲线来描述(表1)。

参数赋值(参数取值范围的确定)主要有3种方式：集中趋势法(输入如众数-中值-均值或均值-标准差等分布数字特征)、分位数法(输入如P90-P50-P10或P95-P50-P5等分位数值)和范围法(输入最大值，最小值，截断值)(表1)。其中，集中趋势法适用于评价参数样本数据较多的情况，通过样本概率统计得到该参数的假设概率分布模型，读取数字特征直接赋值，简单易操作；分位数法和范围法常用于受勘探程度限制而参数数据较少时，需要评估者依据不同参数特性，结合区域类比、评估经验来综合选择模型赋值。

2.2 资源量主要计算参数确定

2.2.1 含油面积 未钻圈闭综合考虑圈闭闭合面积和圈闭充满度确定含油面积；已钻圈闭利用已钻井油气测试、测井等数据确定油水界面圈定含油面积。在低密度测网下，确定含油面积大小还需考虑地层倾角、断鼻、断块型圈闭遮挡断层的延伸范围及岩性圈闭的岩性尖灭线等变数因素[3-4]。常用的概率分布包括对数正态、正态分布、三角分布。

2.2.2 平均有效厚度 含油气层有效厚度是产层毛厚度、几何校正因子和净毛比3个参数的乘积，其大小受3个变量控制。其中，产层毛厚度大小受储层毛厚度和油柱高度相对大小控制，当储层毛厚度大于油柱高度时，产层毛厚度大致等于油柱高度，当储层毛厚度小于油柱高度时，产层毛厚度大致等于储层毛厚度。由于在整个含油面积范围内产层毛厚度大小不一致(图1)，估算该范围内产层毛厚度的平均值需要采用几何校正因子(GCF)。几何校正因子是反映圈闭形态、油柱高度、产层厚度等因素对平均产层毛厚度影响的系数，可以理解为油水界面以上、任何其他截断(例如基底封闭、顶部储层及侧向封闭)之下的圈闭体积与含油面积和产层毛厚度乘积的比值，即图1中绿色图示部分与虚线图示部分的比值[5-6]。

影响几何校正因子大小的因素主要有2个，一是圈闭形态，二是产层厚度与油柱高度的比值。圈闭形态对几何因子的影响较为直观，在含油面积和产层厚度一定时，圆滑断块的几何校正因子大于平直断块(图2)，平顶背斜的几何校正因子大于椎体背斜等等。

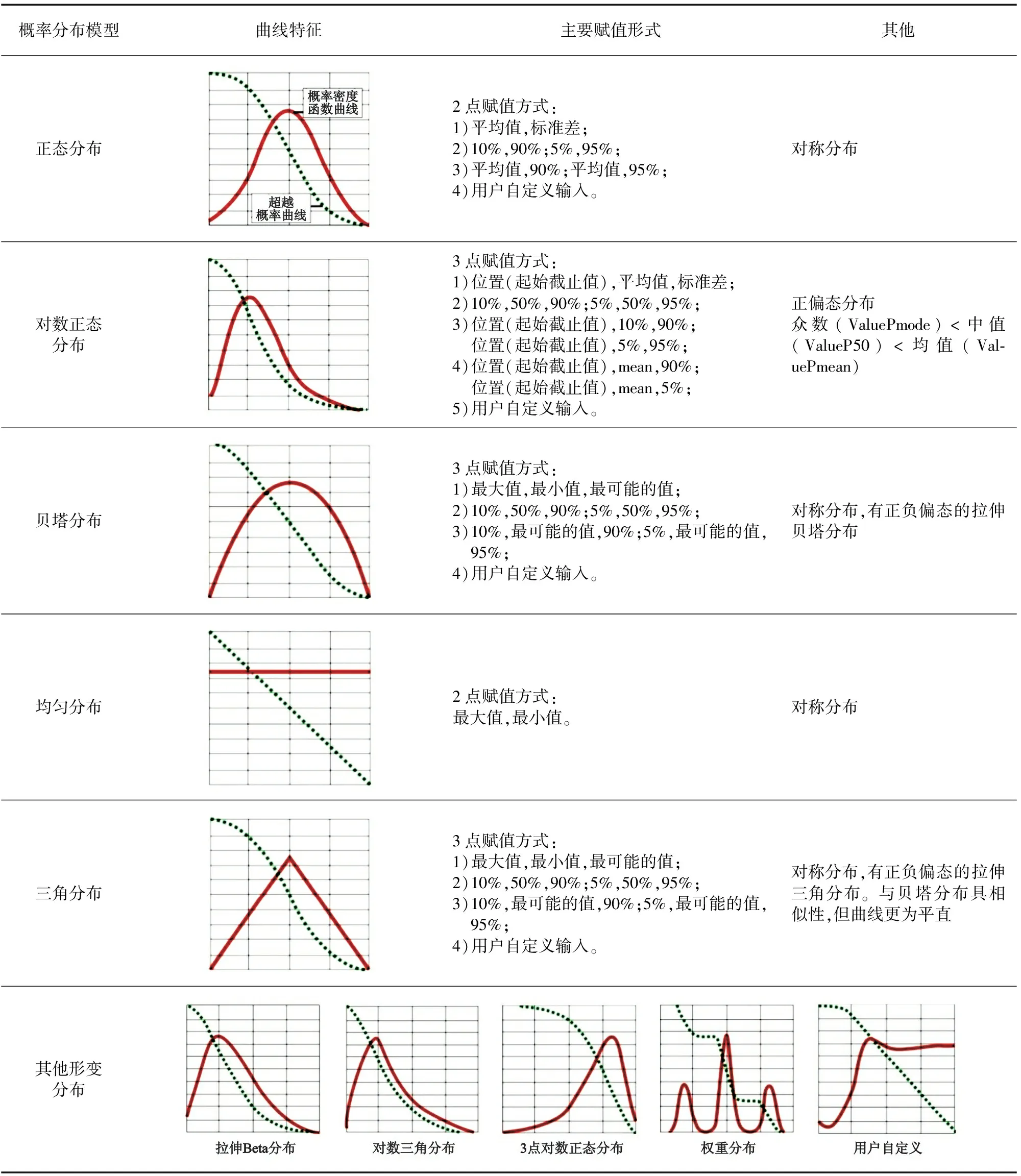
表1 常用的圈闭资源量计算参数概率分布模型及主要赋值形式Tab.1 Probability distribution models and main assignment forms of commonly used calculation parameters of trap resources

产层厚度与油柱高度的比值对几何因子的影响，经过多次测算具有规律性，表现为产层厚度与油柱高度的比值越小，几何校正因子越大(图3)。储层毛厚度与几何校正因子相乘得到含油面积范围内的产层平均毛厚度。净毛比通过测井解释结果来估算，需注意的是储层毛厚度分段方式不同，对应净毛比不同，实际估算中不同分段方式下的参数不能混用[5-7]。据国外一些大公司计算经验来看，有效厚度多选择对数正态分布(油气勘探领域最常用的分布形式)。对数正态分布常与大量划分成更小的过程相关。泥沙沉积符合这一过程[8]。当产层层数较多时，产层厚度多符合正态分布或Beta分布。

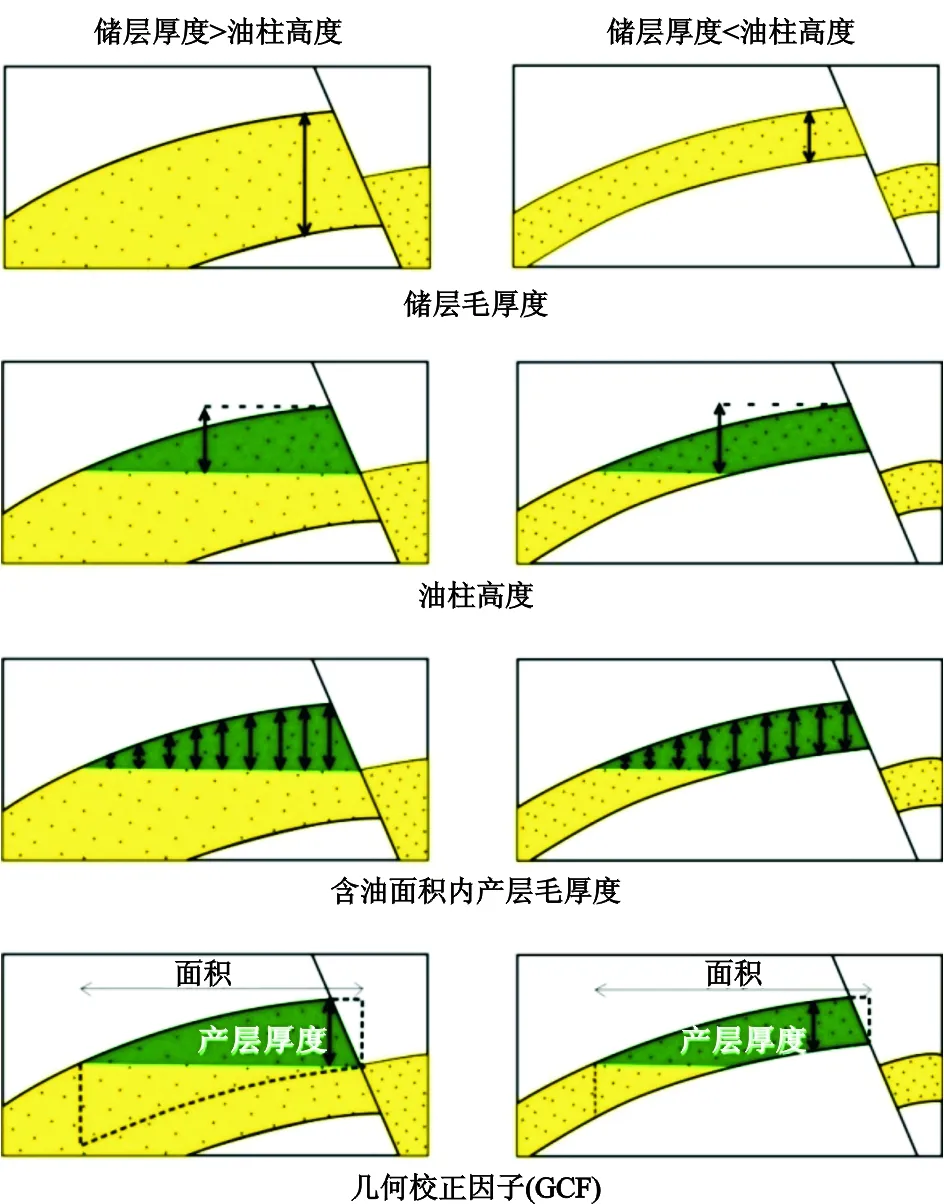
图1 产层毛厚度及几何校正因子示意图Fig.1 Gross reservoir thickness and geometry correction factor of production layer

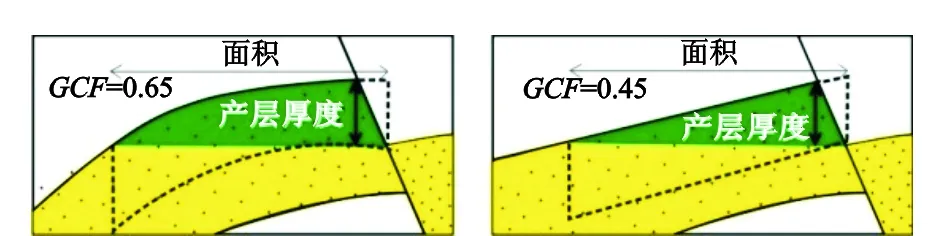
图2 几何校正因子受圈闭形态影响Fig.2 Geometry correction factor affected by the shape of traps

2.2.3 孔隙度、含油饱和度 通常实际油气藏既有岩心分析孔隙度和含水饱和度数据，又有测井解释孔隙度与含水饱和度数据，两套数据不应独立开来，需先用岩心分析数据校正测井解释的孔、饱数据。当研究目标岩心及测井孔、饱参数样本数据较多时，可以通过概率统计直接得到校正后参数的假设概率分布模型。孔、饱参数最常用的概率分布形式为Beta分布。

3 概率分布模型及赋值有效性检验

假设的概率分布模型及赋值是否合理通常可以通过3种方法检验。第1种是函数检验，即通过χ2、A-D、K-S等检验函数做拟合优度检验，拟合程度由拟合误差表示，误差越小，表明样本实际分布与假设分布越一致，假设分布模型越合理；若误差超过一定范围，认为假设有误，其中χ2检验适合用于大样本数据检验，A-D、K-S检验用于小样本数据效果更佳，而K-S检验较之前者敏感性更强[9]。第2种是利用地质含义手段进行检验，常用的检验方式有：①换算出含油气面积的分布极大值P1不应超出实际圈闭的闭合面积；②若平均孔隙度P10值超过0.3时，需要检验孔隙度分布极大值P1是否可能存在(即P1不应大于0.46)；孔隙度分布极小值P99不该小于油气生产的有效孔隙度下限；③含水饱和度最小值即束缚水饱和度通常不会小于0.08～0.10，即油气饱和度分布极大值P1通常不超过0.9～0.92；④各参数P10/P90比值一般不能过高，否则意味着风险过高(不确定性过大)等等。第3种则是利用特定的概率纸根据样本对总体分布的类型进行检验，对连续分布的函数，都可以设计一种坐标纸，使该分布函数在其上的图形成一条直线，概率纸常依概率分布来命名。以对数正态概率纸为例，其横轴为自然对数刻度，纵轴为累计正态概率刻度，服从对数正态分布的样品值在对数正态概率纸上应为一条直线。

4 参数相关性分析

资源评价中地质参数之间的相关性是一个不容忽视的因素，可以确保随机取样符合地质条件间约束。如不考虑，必然会影响资源估算结果的合理性。每个参数都反映了油气资源富集的信息，这些信息彼此之间存在一定的相关性，参数及其相关性共同反映地质总体特征。

如果一个参数随着另外一个参数的增大(减小)而增大(减小)，则这2个参数满足正相关关系；反之，则这2个参数满足负相关关系。相关系数取值范围从-1到1。-1表示最大负相关，1表示最大正相关。取值为0，则表示没有相关性。在实际应用时，对于具有实际井上数据的2个参数，可以利用散点统计法呈现彼此相关性，并量化为相关系数，如孔隙度与含水饱和度、有效厚度与孔隙度等。对于难以统计但理论上存在相关性的参数，则需要根据油气藏具体地质情况结合经验判断确定相关系数,以避免概率模拟出现异常值。

5 软件实现抽样模拟计算

蒙特卡洛模拟是基于数理统计的一种不确定性分析方法，应用蒙特卡洛模拟实现资源量不确定性估算就是通过无数次对各随机变量(各资源量计算参数)抽样，将抽样随机值带入建立好的数学运算(容积法公式)(图4)，其模拟次数越多，精度越高，一般需要成千上万甚至是数十万次试验，但人工不可能实现。常用软件有Crystal ball，是一款广泛用于财政计划、金融投资风险分析及油气风险评估、资源量计算及经济评价等多领域的综合软件[10-11]。利用该软件进行油气资源量计算，需自定义输入参数，即预测自变量(面积、厚度、几何因子等参数)，按文中阐述的方法合理选择概率分布形式后赋值、自定义输出变量及计算方式、设置好参数相关性及模拟运行参数，运行可得到资源量的累积概率分布曲线。

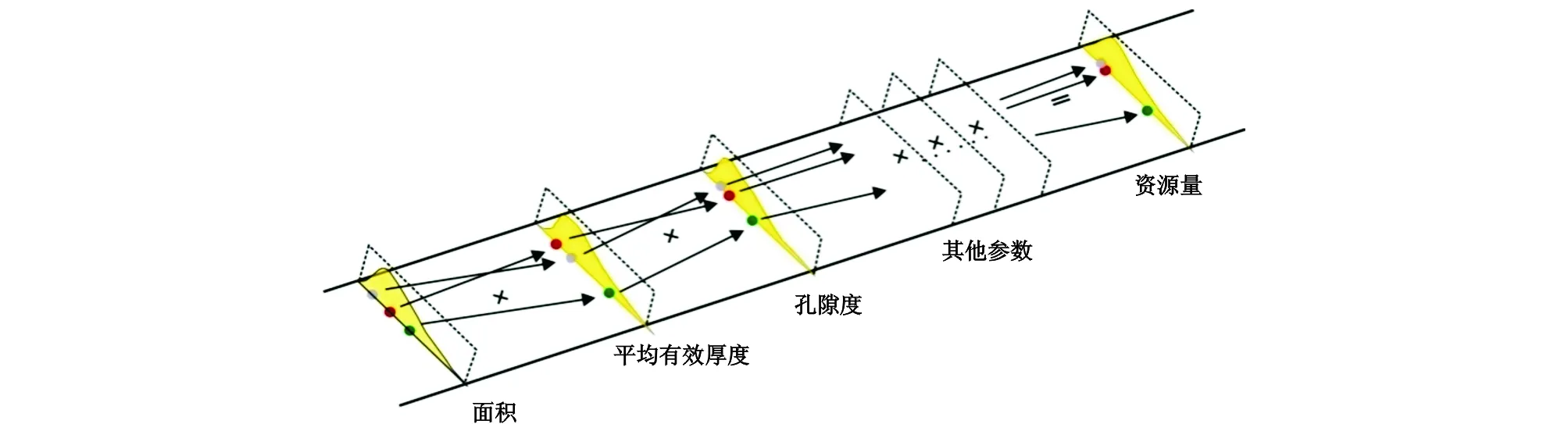
图4 蒙氏模拟计算资源量原理示意图Fig.4 Schematic diagram for calculating resources by using Monte Carlo simulation

6 实 例

圈闭A位于俄罗斯萨哈林岛周边海域的某区块，处于相对隆起背斜构造一翼，区块内构造活动强烈，断层发育，初步识别待评估圈闭为2条断层共同控制的断鼻构造(图5(a))，临近生烃凹陷，主要储层为新近纪上新世海退时期沉积的达吉组多段砂层。已钻井2口，井1失利，井2在Dagi组Ⅰ-Ⅲ砂层获得油流。

利用不确定分析方法对圈闭A达吉组Ⅱ组砂层进行资源量估算。本次估算有效含油面积综合考虑关键断层的延伸长度及圈闭充满程度2个变量，根据二维地震资料东侧断层延伸长度的高中低值为1.50 km,1.75 km,1.97 km，结合区域已钻圈闭充满度和井2已发现油气证据，取圈闭充满度合理高中低值为50%,70%,90%，可得9个面积排列值，将其投在对数正态概率纸(图6)，通过最小二乘法拟合得到的图形近一条直线，验证面积采用对数正态概率分布合理，P90，P50及P10值分别为1.30，1.68和2.18 km2，且此时检验含油面积极大值P01为2.68 km2地质合理。估算平均有效厚度主要考虑产层厚度，油柱高度、几何因子等因素，根据测井解释结果Ⅱ组产层砂层单一，井1及井2厚度分别为25 m和33 m，结合区域对比数据该砂层最大厚度不超过90 m，产层厚度合理高中低值取20 m，30 m，50 m；考虑充满度不同(50%，70%，90%)对应不同油柱高度(约128 m，185 m，250 m)(图5(b))，造成产/油比值大小不同，进一步影响几何因子大小，取几何因子高中低0.9、0.8、0.75，净毛比可取常数1，可得9个平均有效厚度排列值，经概率纸验证符合对数正态分布，其平均有效厚度P90、P50及P10分别为19，27.7和47.3 m(图7)，且对应P01值不大于区域已发现厚度极大值90 m。

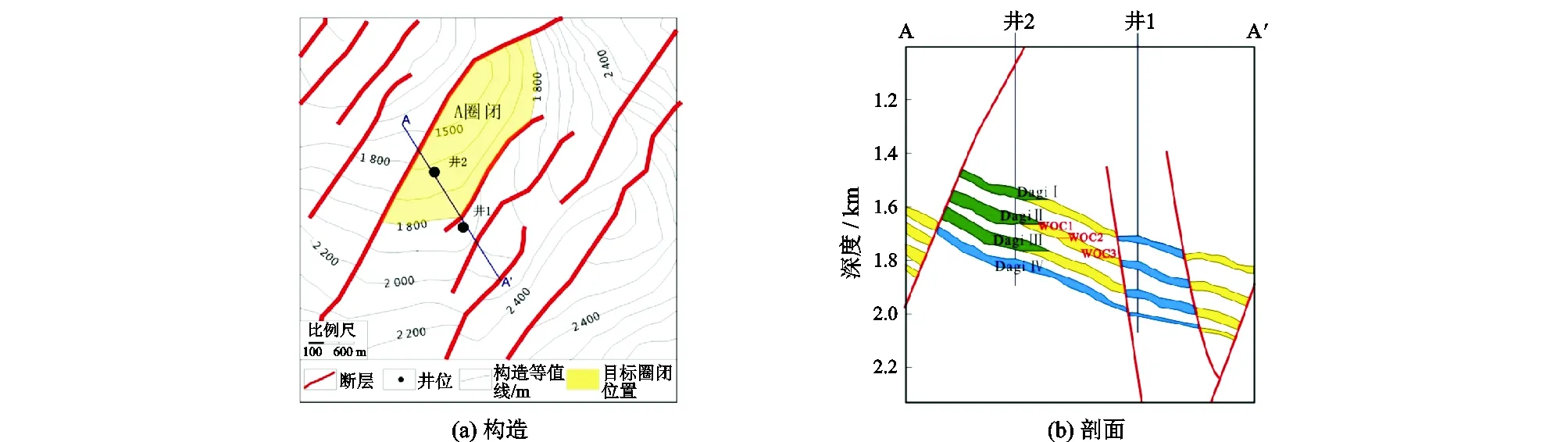
图5 A圈闭Ⅱ段砂层顶面构造及剖面Fig.5 Top structure and section of Ⅱsand layer of trap A

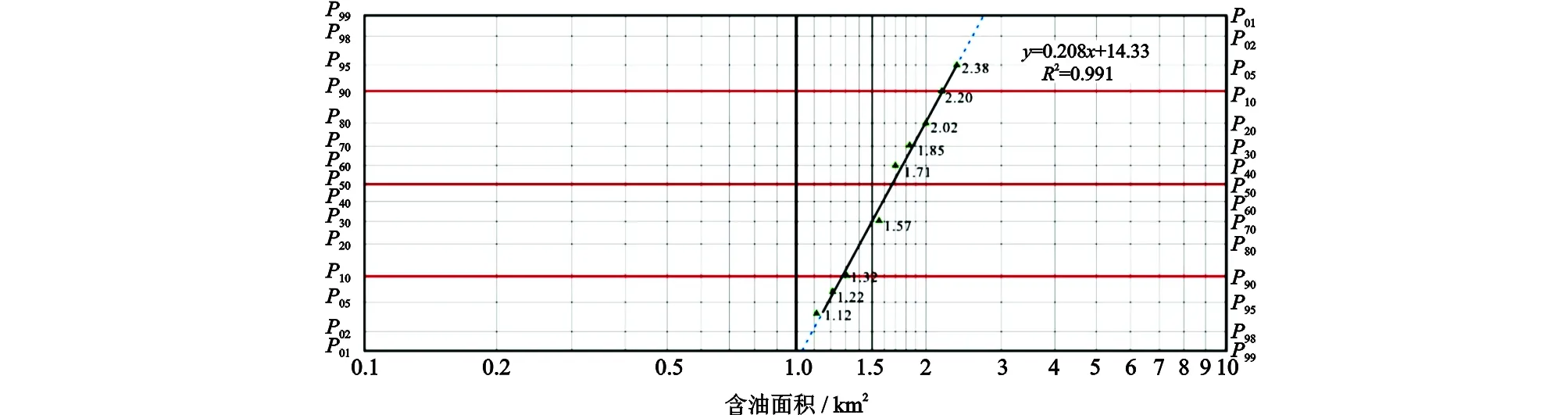
图6 对数正态概率纸上面积值概率分布情况Fig.6 Probability distribution of area values on logarithmic normal probability paper

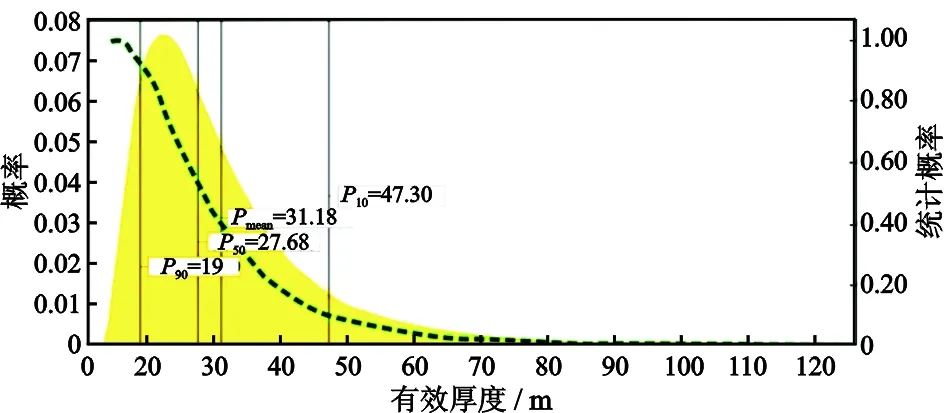
图7 A圈闭Ⅱ砂层有效厚度概率分布模型Fig.7 Probability distribution model of effective thickness of Ⅱ sand layer of trap A

孔隙度借用周边已钻井经岩心校正的测井孔隙度数据做概率统计分析(图8)，确定孔隙度符合拉伸贝塔分布特征，其min，P90，P10及max分别为0.19,0.21,0.28及0.35；同法可得饱和度符合正态分布特征，其P90，P50及P10为0.45,0.55及0.65;体积系数采用常数1.2，密度采用正态分布模型，Pmean为0.88，P10为0.9。

利用散点法分析孔、饱参数相关性，数据点较为分散，没有呈现出明显的递减趋势，得到孔隙度和含水饱和度的相关系数-0.4，表明该油气藏孔隙度与含水饱和度间的相关性较弱。

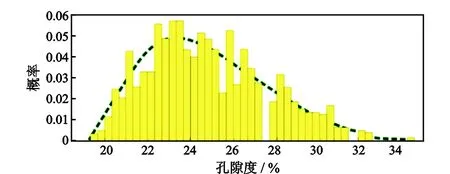
图8 A圈闭Ⅱ砂层有效孔隙度样本概率统计Fig.8 Sample probability statistics histogram of effective porosity of Ⅱ sand layer of trap A

随后利用软件计算Ⅱ段单层圈闭资源量，通过蒙特卡罗迭代模拟得到该段砂组资源量的累积概率分布曲线，资源量P90，P50，P10及均值分别为2.59万t、4.37万t、8.07万t、500万t。

7 结 论

(1)不确定分析法计算圈闭资源量可为项目潜力评估快速提供参考，较确定性算法更为客观，认识更为全面。较建模法，对原始性数据依赖性相对较小，更易实现，是勘探类新项目评价的有效手段。

(2)根据实际地质条件分析资源量计算参数的主要影响因素是准确评估资源量概率分布的前提，如确定有效含油面积需考虑钻井情况、地层倾角、圈闭类型(断鼻、断块型圈闭遮挡断层的延伸范围及岩性圈闭的岩性尖灭线)、钻井程度等因素影响；平均有效厚度受储层毛厚度、圈闭形态、产层厚度与油柱高度的比值和净毛比等因素影响；分析确定孔隙度及饱和度时，要兼顾岩心分析和测井解释数据等等，在工作中要充分合理考虑众多因素。

(3)合理地选择概率分布模型及不确定性赋值受控于资料多少及认识程度。参数样本数据较多的情况，常利用样本概率统计得到合适的概率分布模型；对受勘探程度限制没有实际资料且分布概型没有预知的情况，需要依据不同参数特性，结合区域类比来综合选择模型赋值。本文依据参数特性对主要参数的最常用概率分布类型及检验方法进行了总结，实际选取赋值中应结合适合的方法进行有效性检验，有助于减少评估结果的主观性。

[1] 文环明,肖慈珣,李薇,等.蒙特卡洛法在油气储量估算中的应用[J].成都理工大学学报(自科版),2002,29(5):487-492.

WEN Huanming,XIAO Cixun,LI Wei,et al.Applications of the Monte Carlo method to the petroleum reserves estimation[J].Journal of Chengdu University of Technology(Natural Science Edition),2002,29(5):487-492.

[2] 杨通佑,范尚炯,陈元千,等.石油及天然气储量计算方法[M].第2 版.北京:石油工业出版社,1998:28-29.

[3] 杨双,闫相宾,蔡利学,等.圈闭资源量计算参数确定方法——以断块型圈闭为例[J].石油实验地质,2015,37(4):530-534.

YANG Shuang,YAN Xiangbin,CAI Lixue,et al.Parameter definition in resource calculation of a trap:a fault block example[J].Petroleum Geology & Experiment,2015,37(4):530-534.

[4] 盛秀杰,金之钧,王义刚,等.融合不同地质场景假设的油气区带及圈闭资源量计算方法[J].天然气地球科学,2015,26(3):456-465.

SHENG Xiujie,JIN Zhijun,WANG Yigang,et al.An improved non-deterministic volumetric method for play or trap with quantifying geological scenarios[J].Natural Gas Geoscience,2015,26(3):456-465.

[5] OTIS R M,SCHNEIDERMANN N.A process for evaluating exploration prospect[J].AAPG Bulletin,1997,81(7):1087-1109.

[6] JONKMAN R M,BOS C F M,BREUNESE J N,et al.Best practices and methods in hydrocarbon resource estimation,production and emissions forecasting,uncertainty evaluation and decision making[J].Spe Reservoir Evaluation & Engineering,2002,5(2):146-153.

[7] BEHA A.A general method for the consistent volume assessment of complex hydrocarbon traps[J].Journal of Petroleum Geology,2012,35(1):85-97.

[8] ARPS J J.Estimation of primary oil reserves[J].Petroleum Transactions,AIME,1956,207(8):182-191.

[9] 黄学斌,李军,闫相宾,等.圈闭资源量参数概率分布及有效性检验[J].石油与天然气地质,2014,35(4):577-584.

HUANG Xuebin,LI Jun,YAN Xiangbin,et al.Probability distribution of parameters for trap resources assessment and its validation[J].Oil & Gas Geology,2014,35(4):577-584.

[10] 胡允栋.基于不确定性分析的油气储量分类与评估方法[D].北京：中国地质大学,2007:128-129.

HU Yundong.Oil and gas reserve classification and estimation on the basis of uncertainty analysis[D].Beijing:China University of Geosciences,2007:128-129.

[11] CHARNES J M.Financial Modeling with Crystal Ball and Excel[M].USA：John Wiley & Sons，Inc，2007：190-213.