盐渍土溶出除盐法中盐运移的数学模型与特征

仇启涵

（住化分析技术（上海）有限公司，上海 200436）

1 前言

2011年3月11日，日本发生的大地震对日本东北地区造成了大规模的损害。其中宫城县仅在农业方面的损失总额就高达5450亿日元，流失、冠水等受害面积约2.4万ha（其中约85%为农田[1]）。主要涉及灌溉排水设施的损坏、地下水盐污染等。其中又以海啸引发的海水倒灌造成的农田土壤盐渍化问题（土壤中的盐浓度过高引起的植物无法生长及枯死的环境问题）最为严重。我国东部滨海地区，尽管没有遭受地震海啸等大规模自然灾害，但由于地势低平加之地下水长年过度开采，海水倒灌问题也十分突出，进而引发农田土壤的盐渍化。在部分农田甚至经常可以看到地表析出结晶盐的现象，对农业生产和生态环境造成了巨大的破坏[2]。

中日两国上述地区由于淡水资源丰富以及灌溉排水条件较好，作为农田盐渍化土壤治理的措施，溶出法除盐技术（在农田地表灌水使土壤中的盐分溶出，然后从排水口排出，如图1）得到了广泛应用。但对灌水量和冠水期的管理基本依靠经验来决定，缺乏科学性依据，治理效果的定量评估也不明确[3]。尹建道[4]等对从盐渍土地表灌水洗脱的规律和效果进行了探讨，但未对盐分从地表面溶出的过程进行研究。

本研究根据土壤中物质运移理论构建盐溶出过程的数学模型，并通过室内模拟溶出除盐实验验证其准确度，以期对现行除盐工程的效果进行科学评估，进而提出效率更高的除盐治理方案。

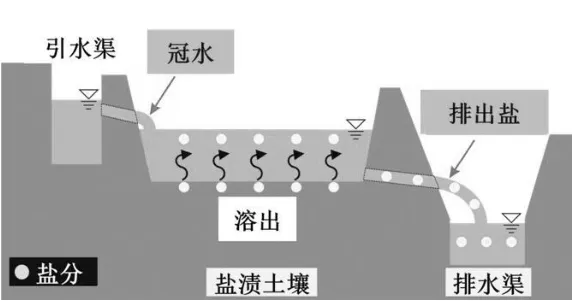
图1 溶出除盐法的原理

2 溶出除盐法的盐运移数学模型

土壤中表示盐运动的扩散方程式如式①：

3 溶出法除盐实验概要

溶出法除盐实验在恒温室（室温22℃）进行，将采自盐渍化农田的供试土壤（粉质黏土）以干密度1650kg/m3填充于丙烯酸树脂圆柱（内半径76mm，长100mm）后，在防止蒸发的同时利用盐水通过毛细管作用从土柱下方使其饱和。之后，将带有排水口（高3mm，直径3mm）的圆柱与土柱连接，并将两极传感器（CS655，Campbell Scientific制）设置在土壤表面以下5mm、10mm、20mm、50mm及85mm的位置。同时，为了测定冠水的盐浓度，在地表面0mm，地表上方10mm、30mm及50mm处设置四极传感器（Sankei理化制）。根据冠水深度hw的变化适当调整冠水中传感器的位置。

实验步骤如下所述：

（1）在不扰动土壤的情况下，用胶头滴管在土柱表面灌入一定量的淡水，静置168小时。

（2）用2台数据记录器（Campbell Scientific和M.C.S产）以每1分钟的频率记录下土壤和冠水中的温度、盐浓度C（Cl-质量/水的体积，kg/m3，以下简称“盐浓度”）。

（3）冠水结束后，用滴管收集从排水口流出的盐水和地表残留水，通过电量滴定式盐分分析仪（salmate-100，Asahi Life Science产）测定C。

（4）往土中铅直插入钢管（内径20mm，长100mm），对不同深度的土壤进行采样。

（5）完全干燥各样品，计算其θ

4 实验结果和模拟计算结果的比较

4.1 盐溶出特征

续升高，各zw处的浓度差逐渐减小，48小时后可忽视浓度梯度的存在（dCw/dz ≒ 0）。hw=100mm时，72小时后zw=0mm与100mm间Cw的差随时间变小。说明与深度无关冠水的盐浓度梯度随时间逐渐减小，冠水深度越低Cw达到相同的时间就越短。

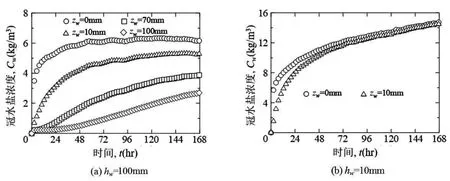
图2 冠水盐浓度的时间变化

图3 （a）和（b）分别表示hw= 60mm和10mm时Cs的时间变化。两者的Cs均随时间减小，地表面以下20mm内的Cs下降很明显，特别是在起始的48小时内。此外，越靠近土壤表面Cs的时间降低率越大。

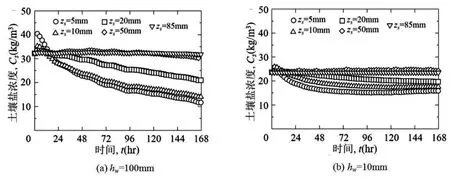
图3 土壤盐浓度的时间变化

4.2 溶出系数α

该数学模型中的溶出系数α是决定溶出量计算精确度的重要参数。Brutsaert[5]在研究水分从湖面向大气中蒸发的速度时引入了通量系数。根据v = α（Cs_surf- Cw）从实验结果反推计算出α的值。因很难精确测得地表盐浓度Cs_surf和紧邻地表面处的冠水盐浓度，所以准确求得α值也比较困难。该模型通过将计算得到的Mt的时间变化与实验测定结果进行曲线拟合来确定α的值。通过计算得出α的值为1.5×10-4～9.0×10-4m/h，与实验中得到α的值的阶（10-4m/h）相同。

4.3 数学模型的改良

式④和式⑤推导的前提条件是冠水中的盐分分布达

由于Cw的时间性变化，Cs_surf和Mt也随时间而变。此处假设Cs_surf和Cw即使发生空间变化式④和式⑤依然可用，以微小时间间隔（Δt=1min）计算Cs（z, t）、Cw（t）和Mt（t），其计算流程如图4所示。

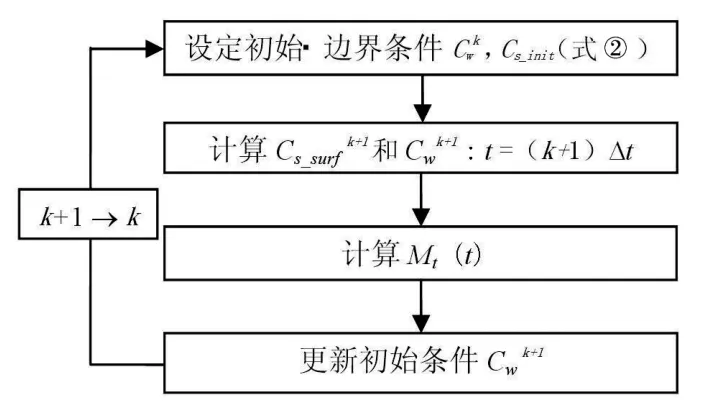
图4 模型计算流程

4.4 模拟计算结果

因假设冠水中的盐为完全混合状态，故本文只对浓度梯度较小的hw=10mm时进行模拟计算。图5分别表示地表面下zs=5mm、10mm、20mm和50mm处Cs的时间变化实验值（圆点），旧模型（Cw=固定值）的计算值（虚线）和本模型的计算值（实线）。旧模型由于未考虑冠水中盐浓度的增加，溶出过程被过大计算，各深度处Cs的减小迅速，168小时后zs=5mm和10mm的计算值分别约为其实验值的1/3和1/2。而本模型的计算值与实验值基本一致，但是zs=5mm和10mm处两者的差比其他深度处的差大，推测是地表的土壤出现过饱和，是传感器的输出值与盐浓度之间换算偏大造成的。因此，需要对传感器在过饱和土壤中的输出值与盐浓度之间的函数进行再拟合，校正zs=5mm和10mm处的实验值。

图6表示hw=10mm时累积溶出量Mt的时间变化（圆点、虚线和实线的含义与图5相同）。使用旧模型计算的话，Mt同样出现结果偏大的现象，168小时后约为实验结果的2.5倍。而使用式④和式⑤组合构成的模型进行的计算值则很好地再现了实验值。

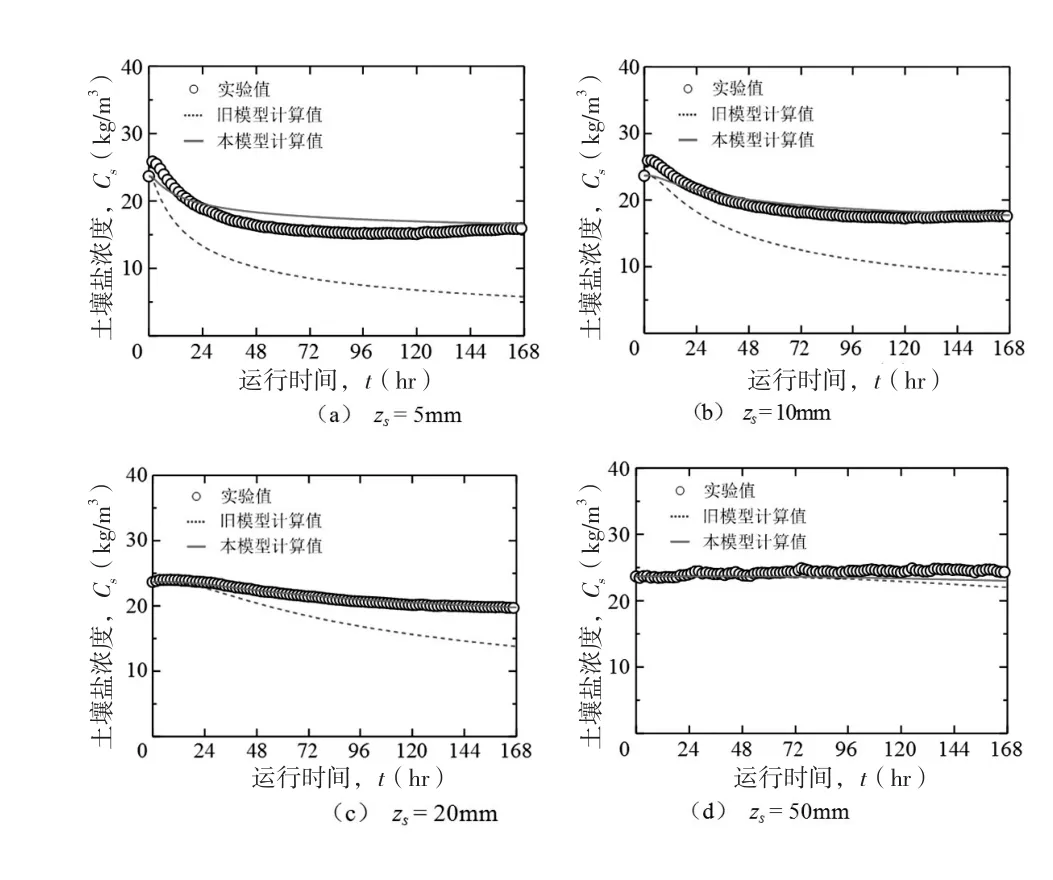
图5 土壤中盐浓度时间变化的实验和计算结果的比较

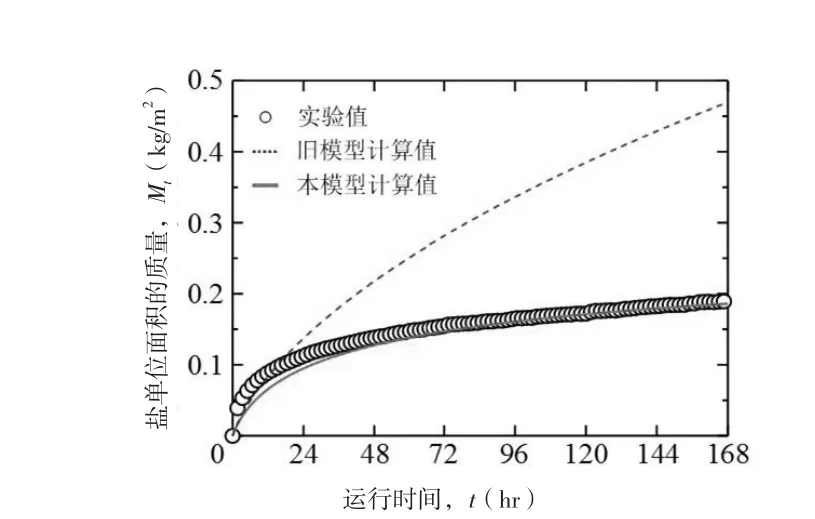
图6 累积溶出量的实验和计算结果的比较（hw=10mm）

5 不同冠水深的累积溶出量的评价

图7表示hw=10～500mm不同冠水深时利用本模型计算的Mt的时间变化情况。此处以hw=10mm为基准，将各hw的Mt除以hw=10mm时的累积溶出量（Mt10）得到的值R（-），进行标准化。各hw的R均随时间增大，但R的增大率逐渐减小。另外，hw越高R越大，168小时后hw=30mm、50mm、100mm、200mm和500mm的Mt分别约为Mt10的1.5倍、1.8倍、2.1倍、2.3倍和2.4倍。冠水深即使从hw=100mm增加到200mm，除盐效率也仅提高了10%。由此可知，虽然冠水深越大除盐效率越高，但所需的冠水期较长。从水的利用率和排水时间的角度来说，无需在地表灌溉100mm深以上的水。

图7 不同深度冠水时累积溶出量的计算结果

6 结论

本研究通过室内土柱实验定量评价了盐溶出特征。根据其结果，将盐浓度伴随溶出过程逐渐增加的因素考虑在内，对基于物质扩散方程式构建的盐运移数学模型进行了改良，并验证了改良模型的适用性。然后通过模拟计算讨论了冠水深度对累积溶出量的影响。主要结论为：

（1）在盐溶出过程中，越靠近地表面的土壤盐浓度下降越显著；

（2）冠水中在铅直方向存在盐浓度梯度，冠水深越小达到全域混合状态的时间越短；

（3）溶出的盐在冠水中达到均匀混合状态时，只要准确求得溶出系数α，即可利用本模型大致预测溶出盐量和土壤中盐浓度的分布；

（4）冠水中不发生对流时，α的阶为10-4m/h；

（5）冠水深度越大越促进盐溶出，但100mm以上时促进效率增加很小。

在今后的研究中，将对实际农田盐渍化土壤治理效果进行监测，并利用本模型计算验证其在实际工程中的适用性，预测工程开展过程中土壤的水盐运移，进一步提出高效的溶出法除盐治理方案。

[1] 日本农林水产省. 平成23年度 粮食·农业·农村白皮书[R]. （2012-4-24）.

[2] 李怒云，龙怀玉.植树造林与21世纪盐渍土开发利用的关系[J].北京林业大学学报，2000，22（3）：99-100.

[3] 一般财团法人日本水土综合研究所.农田的除盐技术研讨会报告书[R].2013， 63-73.

[4] 尹建道，姜志林，曹斌，杨勇，生原喜久雄.滨海盐渍土脱盐动态规律及其效果评价[J].南京林业大学学报，2002，26（4）：15-18.

[5] Brutsaert，W.Hydrology: An Introduction [M].Cambridge University Press， 2005．