测井水位与实际水位的误差分析及进水口设计

吕耀光

（浙江省水文局，浙江 杭州 310009）

1 问题的提出

水位观测是水文测验中最基本也是最重要的内容之一，是河道流量及断面测验的基础。为实时观测水位的变化过程，消除或减少天然河道中水面波浪或短期波涛的影响，通常需要建造水位井。使用自记水位计或其他水位观测装置来记录水位变化过程。

该方法是以水位井内的水位变化情况代表全断面的水位变化情况，因此水位井内的水位变化应尽可能与河道中实际水位变化保持一致。然而，由于水位井具有滞后性以及测井内外水体存在密度差，导致测井水位与实际水位存在误差。

2 井内水位变化滞后现象引起的水位误差

2.1 原理与公式

在天然河道中，水位的涨落变化相对来说是比较缓慢的，以1 h内水位变幅5 m的情况为例，水位变率为0.001 4 m/s，可以忽略不计，因此天然河道的水流近似满足恒定流条件。根据恒定流能量方程[1]，以进水口位置的水平面0 — 0为基准面（见图1），对测井外断面1和测井内断面2列能量方程：

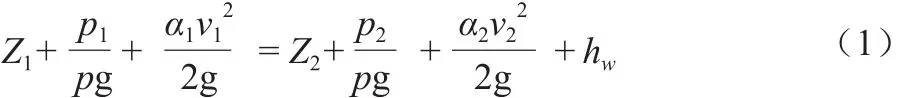
图1 测井在河道中的位置示意图

式中：Z1为河道中的位置水头，即河道实际水位，m；为河道中水面位置的压强水头，m；为河道中水面位置的流速水头，m；Z2为测井内的位置水头，即测井内水位，为测井内水面位置的压强水头，为测井内水面位置的流速水头，m；hw为从断面1到断面2的水头损失，m。

对于天然河道，当进水口处河道流速较大时，行近流速水头将转换为测井内的位置水头，导致测井水位偏高，不符合设井条件，这里不做分析。假定测井设置在靠近岸边水流平缓处，进水口处的行近流速水头；对于进水管道来说，测井容积很大，井内流速水头水面位置并设水位井内水位变化较河道水位变化的滞后量为ΔZ。根据式（1）可得：

对于断面1和断面2之间的水头损失hw，主要由进水管的局部水头损失Σhj和沿程水头损失Σhf组成。

因此，井内水位滞后量ΔZ可用下式计算：

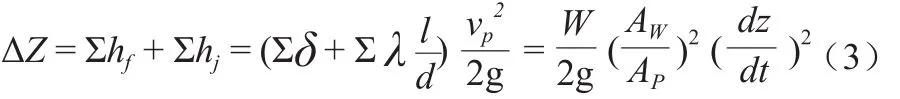
式中：δ为局部水头损失系数；λ为沿程水头损失系数；W 为总水头损失系数[2]l为进水管的长度，m；d为进水管的直径，m；vp为进水管内的平均速度，m/s；AW为测井的横截面积，m2；AP为进水管的横截面积，为水位变率，m/s。当设计测井和进水管时河流最大水位变率；当计算测井滞后量时取测井中实际水位变率。

2.2 计算示例

水位井的进水管形式见图2。假设水位变率的最大值为0.0036 m/s，测井直径为1.00 m，允许测井的滞后量不超过2 cm，进水管采用单式新铸铁管，进水管长度2 m，求进水管的最小尺寸。

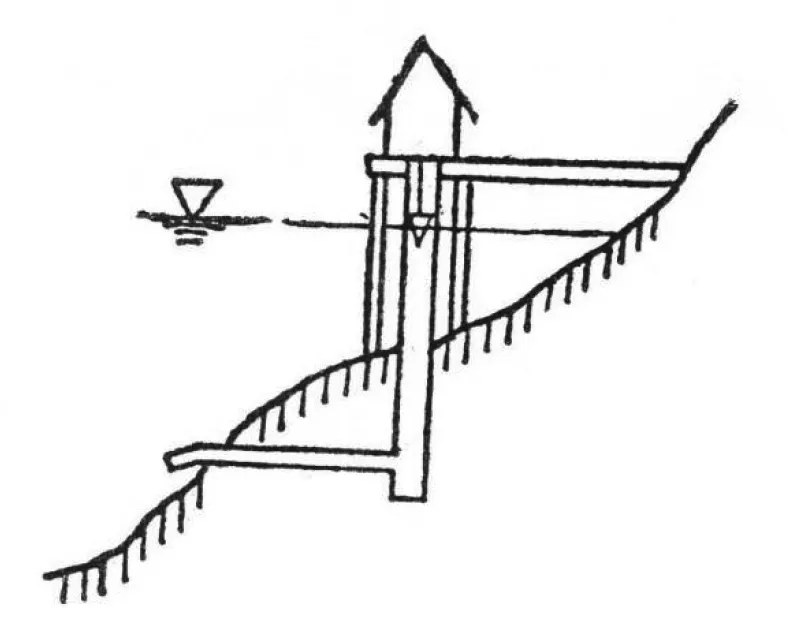
图2 水位井的进水管示意图

进水管的局部水头损失需计算各个部分局部水头损失的代数和。实例中，局部水头损失系数Σδ由进口损失系数δ1、出口损失系数δ2和转弯损失系数δ3组成[1]，即

Σδ = δ1+ δ2+ δ3= 0.5+ 1.0+ 0.2 = 1.7

进水管的沿程水头损失系数根据穆迪图[1]计算。水温20 ℃时，水的运动粘度v = 0.0101 cm2/s，查询管道当量粗糙率ks值表[1]得到新铸铁管的当量粗糙度ks= 0.3 mm。管道最大流速

在假定不同管径d的条件下，计算Re和ks/d值，根据穆迪图查询对应的值，得到不同管径d相对应的表1）。

表1 不同管径d对应的管道沿程水头损失系数值计算表

采用试错法开展管道直径d计算，假定d = 0.10 m，则3由公式（ ）转换可得：

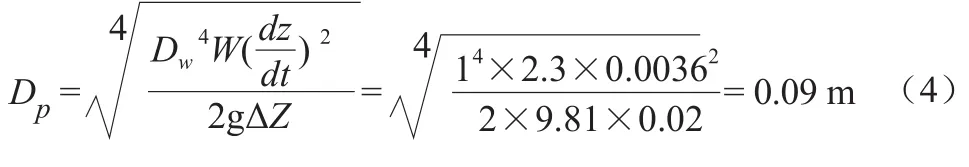
根据上述计算，进水管的计算管径Dp与假设管径d基本一致，试错法假设条件成立，试算完成。综上得出结论，进水管的设计直径应不小于0.09 m。

在实际应用中，应根据测井及其进水口的具体情况，计算符合实情的局部水头损失系数和沿程水头损失系数，再查询实际断面上的水位最大变率和测井的允许滞后量，并由此进行测井和进水管的尺寸设计计算。

3 测井内外水体密度差异引起的水位误差

3.1 原理与公式

假设进水管的入水深度为H，m；r水为清水密度，kg/m3；r泥沙为泥沙密度，可采用2.65 t/m3计算[3]；Cs为含沙量，kg/m3。为分析测井内外水体密度差异对井内水位变化的影响，假定井内水体清澈，近似为清水，井外则为浑水。即可得出：

体积为V浑水的浑水内所含悬移质泥沙的体积

体积为V浑水的浑水内所含清水的体积V清水=V浑水-Vs；

则浑水密度

不考虑测井内水位变化滞后现象引起的井内水位误差，选择水位涨率相对较小的时刻进行分析。此时，动水压强的分布近似满足静水压强的分布规律，得出：

式中：Hw为井内水面至进水管的深度，m。

根据公式（5）和公式（6），测井内外水体密度差异引起的水位差ΔZ可用下式计算：

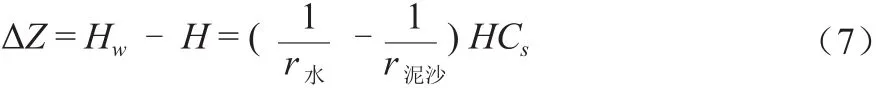
3.2 计算示例

之江水文站涨潮前的水流清澈[4]，而大潮汛时最大含沙量可达4 kg/m3，历史最高潮位可达7.00 m，要求测井内的水位误差不能大于2 cm，求进水管的安装高程（不考虑井内水位变化滞后现象）。

大潮汛时期，井内水体在短时间内来不及交换，近似为清水。由式（7）可得进水管最大水深H：

根据之江站的实际水文特性，历史最高潮位为7.00 m，故进水管的安装高程不应低于- 1.03 m。

几种不同含沙量、进水口深度和水位差计算结果见表2，可供设计时查询使用。

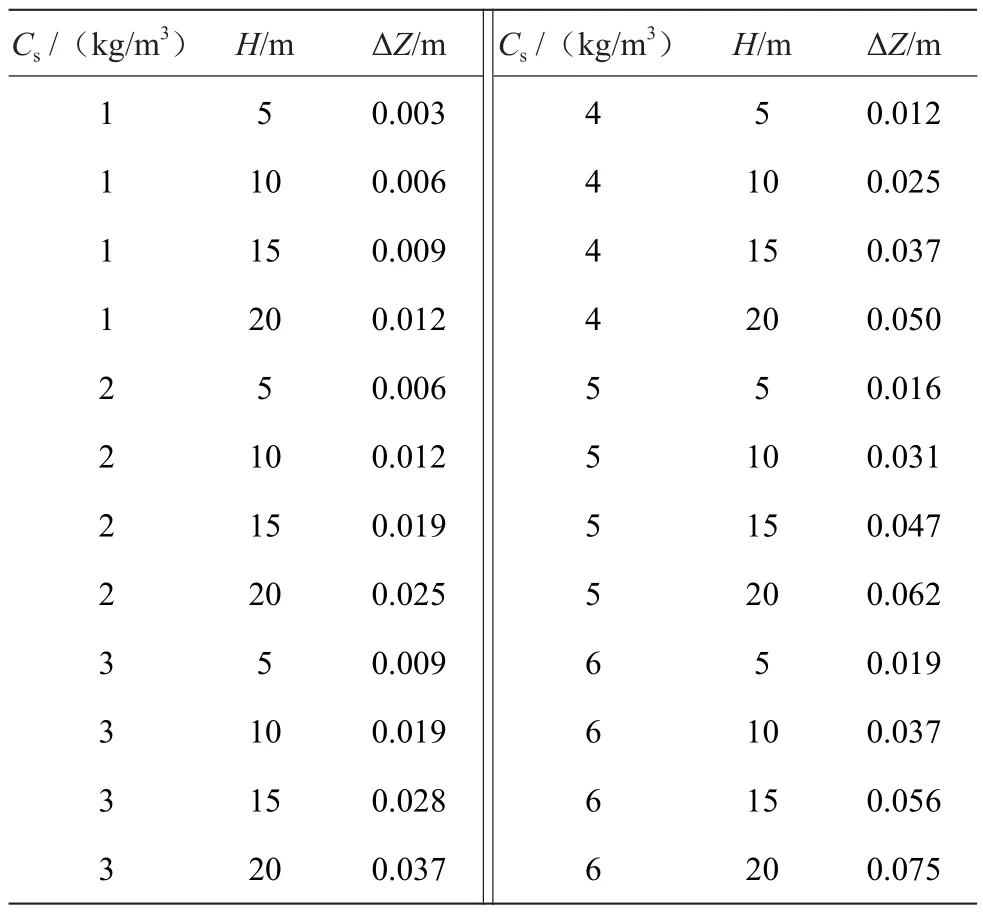
表2 不同含沙量Cs、进水口深度H和水位差ΔZ计算结果对照表

4 结 论

（1）对测井水位与实际水位的误差进行分析，证实水位井的滞后作用和测井内外水体密度差异是影响测井水位误差的2大来源。

（2）在已知最大水位变率和允许测井滞后量条件下，可进行水位测井和进水管尺寸的设计计算；在已知河道最大含沙量和允许测井误差量条件下，可进行进水管安装高程的设计计算。

（3）根据本文的计算方法，各站结合自身测站特性，即可实现各自水位测井的进水管样式尺寸和安装高程等的设计计算，为水位台选型设计提供依据。

[1] 赵振兴，何建京.水力学[M].北京：清华大学出版社，2005.

[2] 丁兵，昝学才，周春天.复管进水口水位自计井滞后量计算[J].南昌工程学院学报，2005，24(1)：60 - 62.

[3] 林传真，周忠远.水文测验与查勘[M].南京：河海大学出版社，1987.

[4] 吕耀光，黄士稳.钱塘江河口区声学多普勒测流及资料整编[J].河海大学学报(自然科学版)，2010，38(6)：680 - 687.