对称矩阵填充的线性交替最速下降算法研究
韩如意, 王川龙
(1. 太原理工大学 数学学院, 山西 太原 030024; 2. 太原师范学院 数学系, 山西 太原 030619)
0 引 言
随着互联网公司 (如Google, 360, 百度, Netflix) 的快速发展, 搜索引擎也逐渐在普及, 使得数据的收集越来越方便, 数据量猛增, 大数据概念被越来越广泛提及, 而这些大量的数据蕴含着非常重要的信息. 所以, 如果能充分运用好这些数据信息, 将会为自身的发展, 公司的利益和社会的进步带来巨大的推动作用. 既然大数据对社会和人们的实际生活有重大的价值, 那么就会出现因各种原因而导致的整体数据不完整的现象, 研究如何将这些缺失的数据补充完整也将变得越来越重要. 这就是矩阵填充问题.
矩阵填充问题近几年发展迅速, 它主要研究的实际问题是如何在矩阵元素缺失的情况下通过已知的部分元素精确地填充这些缺失元素, 从而将原矩阵填充完整. 著名的Netflix推荐系统[1]就是矩阵填充问题的一个典型应用. 在图像恢复[2], 机器学习[3], 计算机视觉[4], 控制[5]等信息科学领域矩阵填充发挥着重要的作用, 并且其在系统识别[6], 频谱感知[7], 多媒体编码和通信[8]等方面也有应用.
对于矩阵填充问题有如下模型,
minrank(Z)
s.t.PΩ(Z)=PΩ(Z0),
(1)
式中:Z∈Rn1×n2;Z0∈Rn1×n2且Z0是采样矩阵;Ω⊂{1,…,n1}×{1,…,n2} 为已知的样本元素下标集;PΩ为集合Ω的正交投影. 该问题的意义在于将缺失的元素填充后使得矩阵的秩尽可能的低. 近年来, 在已知矩阵秩r的前提下, 人们提出许多算法, 如黎曼信赖域法(Riemannian trust-region method, 简称 RTRMC[9]), OptSpace 算法[10], ADMiRA算法[11].
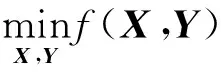
(2)
为求解模型(2) , 人们提出一种交替最小算法PowerFactorization, 简称PF[12]. 而算法PF中的每次迭代实际上是求解一个标准的最小二乘问题, 这样不仅带来高的迭代计算成本, 还降低了计算效率. 为了改善这个缺陷, 人们提出另一种交替最小算法Low-rankMatrixFitting, 简称LMaFit[13]. 2015 年,TannerJ等[14]提出了交替最速下降法 (AlternatingSteepestDecent, 简称ASD).ASD比PF的迭代计算成本低很多, 精度更高; 比起LMaFit,ASD能更好地填充高秩矩阵, 并通过数值实验也进一步证明了ASD算法的可行性和有效性.
在文献[14]中, 用ASD算法对一般低秩矩阵进行了填充. 而在实际中, 采样矩阵往往也会有许多特殊结构的矩阵, 其中对称矩阵就是特殊结构矩阵中的一种, 并且对称矩阵在通信工程和电力系统等诸多工程应用领域中也发挥着重要作用. 因此研究对称矩阵填充问题很有意义.
本文主要研究对称矩阵的填充问题, 并结合最优化中的非精确线性搜索方法来搜索最优步长, 不仅从理论上证明该算法的可行性, 而且通过不同采样率的矩阵填充数值试验展示该算法的可行性和有效性.
为方便, Rn1×n2表示n1×n2实矩阵全体. ‖Z‖*表示矩阵Z的核范数, ‖Z‖F表示矩阵Z的Frobenius范数,ZT表示矩阵Z的转置. 矩阵X和Y的内积用〈X,Y〉=trace(XTY) 表示. 集合Ω⊂{1,…,n1}×{1,…,n2}表示采样矩阵已知元素的下标集.PΩ表示集合Ω上的正交投影.
本文第1节详细介绍了非精确线性搜索方法和提出的对称矩阵填充算法; 第2节分析了算法的收敛性; 第3节通过取不同的采样率进行数值试验, 进一步验证了算法的可行性和有效性; 第4节总结全文.
1 算 法
本节介绍基于非精确线性搜索的交替最速下降算法去填充一个秩为r的对称矩阵.
引理 1[15]在数域P上, 任意一个对称矩阵都合同于一对角矩阵. 于是, 对称矩阵填充问题可以描述为如下模型
(3)
式中:Z0∈Rn× n且为对称矩阵,X∈Rn× r,D∈Rr× r且为对角矩阵.
为了提高算法PF中最小二乘问题的计算效率, 本文算法采用了沿梯度下降方向简单的线性搜索方法. 设fD(X)表示f(X,D)对X的梯度;fX(D) 表示f(X,D) 对D的梯度. 于是梯度上升方向为
fD(X)=-2(PΩ(Z0)-PΩ(XDXT))XD,
(4)
沿梯度下降方向的最优步长也能被准确地计算.
引理 2 设tx,td是下降方向-fD(X) 和-fX(D)对应的最优步长, 则
(5)
而tx不能被精确求出, 于是用最优化中的非精确线性搜索方法求解.
g′(td)=〈PΩ(Z0)-PΩ(X(D-tdfX(D))XT),XfX(D)XT〉=〈PΩ(Z0)-PΩ(XDXT)+
tdPΩ(XfX(D)XT),XfX(D)XT〉=〈PΩ(Z0)-PΩ(XDXT),XfX(D)XT〉+
td〈PΩ(XfX(D)XT),XfX(D)XT〉=〈(PΩ(Z0)-PΩ(XDXT))X,XfX(D)〉+
td〈PΩ(XfX(D)XT),XfX(D)XT〉=〈XT(PΩ(Z0)-PΩ(XDXT))X,fX(D)〉+
td〈PΩ(XfX(D)XT),PΩ(XfX(D)XT)〉=〈-fX(D),fX(D)〉+td〈PΩ(XfX(D)XT),
PΩ(XfX(D)XT)〉=-‖
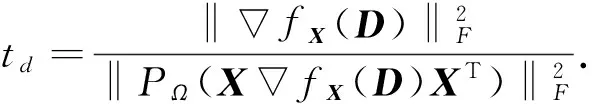
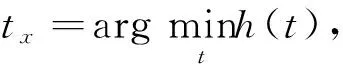
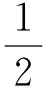
(6)
显然h(t)是关于t的四次函数, 我们用最优化中的非精确线性搜索方法求解.
在最优化中求步长的非精确线性搜索方法很多, 经过多次试验, 最后选择带保险措施的简单准则来搜索. 在给出该搜索方法之前, 做如下说明:
设φ(tx)=h(tx), 则
tx2PΩ(fD(X)D
tx(PΩ(XDfD(X)T)+PΩ(fD(X)DXT))-tx2PΩ(fD(X)DfD(X)T),
(7)
于是
(8)
φ′(tx)=〈PΩ(Z0)-PΩ(XDXT)+txPΩ(XDfD(X)T+fD(X)DXT)-
tx2PΩ(fD(X)DfD(X)T),PΩ(XDfD(X)T+fD(X)DXT)-
2txPΩ(fD(X)DfD(X)T)〉=trace((PΩ(Z0)-PΩ(XDXT)+txPΩ(XDfD(X)T+
2txPΩ(fD(X)DfD(X)T))),
(9)
则
φ′(0)=trace((PΩ(Z0)-PΩ(XDXT))TPΩ(XDfD(X)T+fD(X)DXT)).
(10)
这样非精确线性搜索中带保险措施的简单准则如下:
1) 选取初始数据.tx=1,ρ=0.1,a=0.5, minstep=10-5,k∶=1.
2) 检验准则. 计算φ(tx),φ(0),φ′(0).
如果φ(tx)≤φ(0) +ρtxφ′(0), 停止, 输出tx; 否则, 转第 3) 步.
3) 检验保险措施.
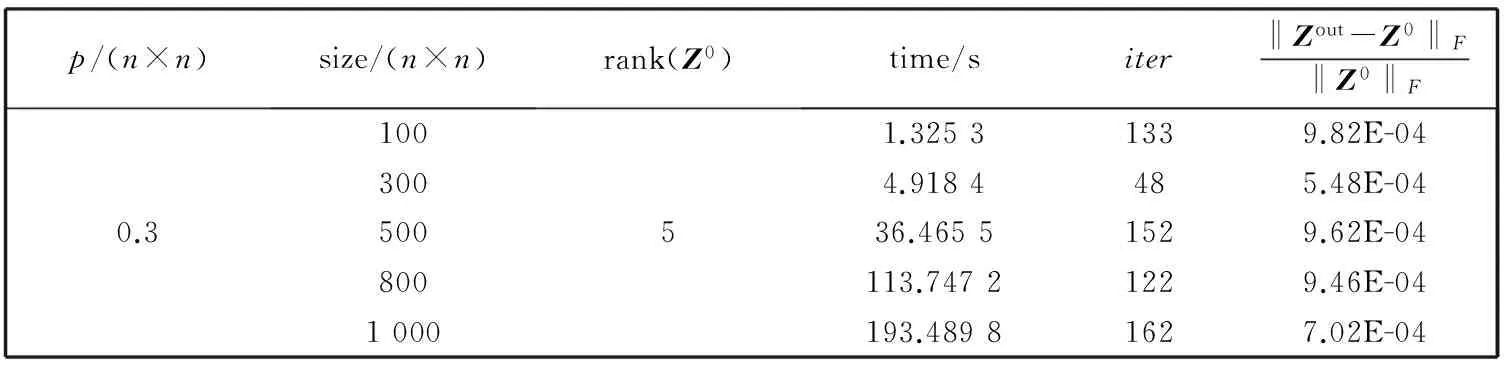
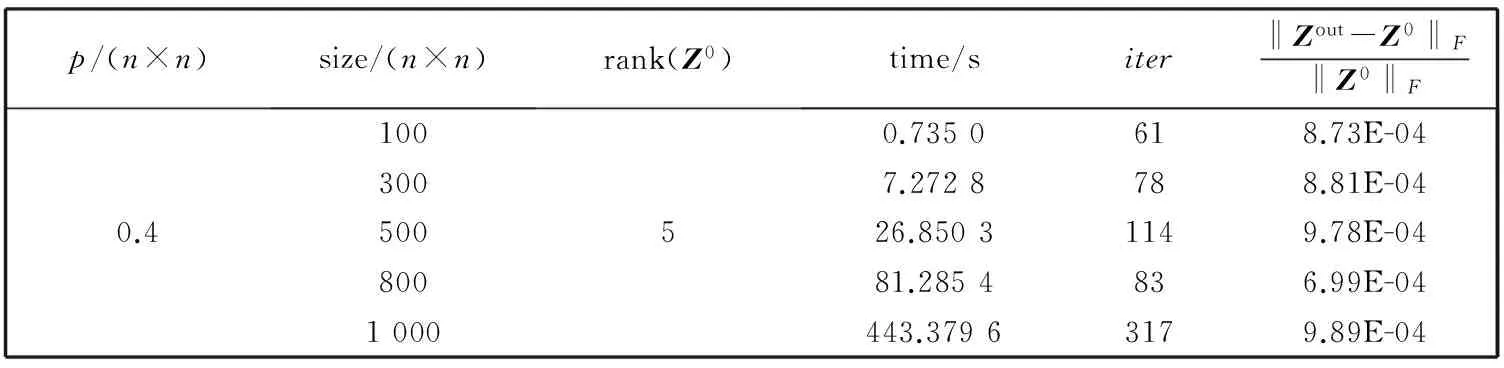
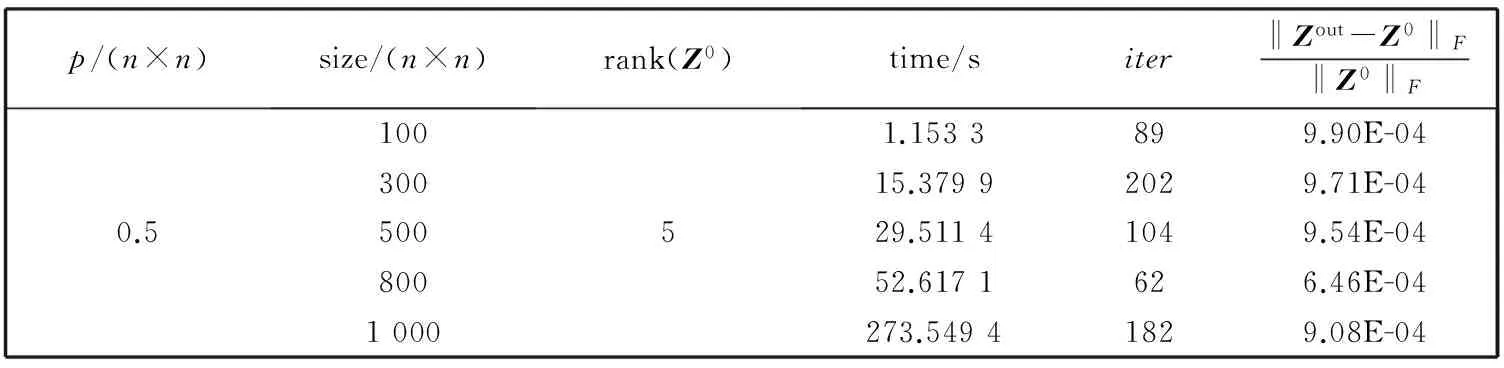
如果 ‖tx(-fD(X))‖2 4)tx=atx,k∶=k+1, 转第 2) 步. 以上引理2和非精确线性搜索中带保险措施的简单准则给出沿负梯度方向的最优步长, 接下来介绍对称矩阵填充算法的具体实施过程. 算法 1 基于非精确线性搜索的交替最速下降算法. 1) 给定矩阵大小n×n, 秩r, 采样密度δ, 采样个数p, 样本矩阵PΩ(Z0), 初始矩阵X0,D0,ε>0,k∶=1. 2) 计算梯度方向和相应的步长, 更新X0,D0. fDk(Xk)=-2(PΩ(Z0)- PΩ(XkDkXkT))XkDk, tx用非精确线性搜索方法求解, Xk+1=Xk-txfDk(Xk), Dk+1=Dk-tdfXk+1(Dk). 5)k∶=k+1, 转第 2) 步. 本节在一定条件下证明了算法1的收敛性. 为方便,dx和dd分别对应X,D的方向, 即负梯度方向;tx,td分别表示沿负梯度方向搜索到的最优步长. 由于问题(3)的特殊结构, 结合算法中求步长的规则(5), 能直接证明算法的极值点就是问题(3)的稳定点. 也就是说, 极值点(X,D)满足 fD(X)=0,fX(D)=0. (11) 定理 1 设(Xi,Di)是算法1生成的序对, 且在每次迭代中都是非奇异的. 设 (Xik,Dik)是(Xi,Di)的子序对且对于一个非奇异序对 (X*,D*)都有 则(X*,D*)是稳定点, 即满足式(11). 为了证明定理1, 由梯度的连续性, 只须证明 接下来, 利用以下引理3和引理4来证明. 引理 3 收敛于(X*,D*) 的定理1中的子序对(Xik,Dik)有界, 且满足 (12) f(Xi,Di-1)=f(Xi-1,Di-1)+〈fDi-1(Xi-1),Xi-Xi-1〉= f(Xi-1,Di-1)+〈fDi-1(Xi-1),txi-1dxi-1〉= f(Xi-1,Di-1)+txi-1〈fDi-1(Xi-1),dxi-1〉≥ (13) (14) 取式(13)下界并从i=0到i=l对式(13)~(14)求和得 而对所有的l, f(Xl,Dl)非负, 于是 则 (15) 将dxi和ddi-1代入式(15)得 (16) 即 (17) 特别地, 将i换成ik, 式(17)也是成立的, 即 (18) 因为Xik,Dik有界, 于是 ‖PΩ( (19) ‖PΩ(Xik ‖Xik‖F‖fXik(Dik-1)‖F, (20) 式中:C>0. 结合式(18)~(20)有 (21) 引理 4 定理1中的子序对(Xik,Dik)满足 (22) 所以 ‖fXik(Dik)- (23) 本节通过数值实验给出非精确线性交替最速下降算法对低秩的对称矩阵填充的实验结果, 所有的数值实验均是在相同的工作环境下进行的. 算法结果见表 1~3.p/(n×n)表示采样密度, 其中p是已知元素的个数.Zout表示得到的填充矩阵,Z0表示采样矩阵. 在本文算法中, 参数δ∈{0.3,0.4,0.5},ε=10-3. 此外, 用s表示时间单位,iter表示迭代次数. 表 1 取样为0.3的填充结果 表 2 取样为0.4的填充结果 表 3 取样为0.5的填充结果 表 1~表 3 展示了不同采样密度的低秩对称矩阵的填充数值结果, 结果表明该算法是可行的. 随着矩阵规模的增大, 计算时间将增大. 但是由于实验中随机产生的样本矩阵和采样密度, 造成矩阵完成的复杂度有差异. 为了展示同一样本矩阵在不同采样密度下的完成结果, 进行了表 4~表 8 的测试. 表 4 矩阵大小为100×100的填充结果 表 5 矩阵大小为300×300的填充结果 表 6 矩阵大小为500×500的填充结果 表 7 矩阵大小为800×800的填充结果 表 8 矩阵大小为1 000×1 000的填充结果 从表 4~表 8 可以看到相同环境下同一矩阵在不同采样密度下的具体填充实验结果. 发现随着采样密度的增加, 填充时间和迭代次数也随着增大, 这在理论分析上也是合理的. 本文基于一般矩阵填充的ASD算法对具有特殊结构的对称矩阵填充进行了研究. 将对称矩阵进行简单因式分解, 用ASD算法中的求导思想找到最优下降方向, 然后求出相对应的步长. 对于不能精确求解的步长, 提出用最优化中的非精确线性搜索方法来搜索最优步长, 进而迭代更新形成新矩阵. 理论上给出了算法的收敛性分析, 表 1~8 的数值实验结果也验证了算法的可行性和有效性. 同时还可以看到, 填充的矩阵规模相对较小, 希望可以继续探讨更大规模矩阵的填充算法, 这将是今后需要研究的问题. [1]Bennett J, Lanning S. The netflix prize[C]. Proceedings of KDD Cup and Workshop, 2007: 35. [2]Bertalmio M, Sapiro G, Caselles V, et al. Image inpainting[C]. Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, 2000: 417-424. [3]Schölkopf B, Platt J, Hofmann T. Multi-task feature learing[C]. Conference on Advances in Neural Information Processing Systems, 2006: 41-48. [4]Tomasi C, Kanade T. Shape and motion from image streams under orthography: a factorization method[J]. International Journal of Computer Vision, 1992, 9(2): 137-154. [5]Mesbahi M, Papavassilopoulos G P. On the rank minimization problem over a positive semidefinite linear matrix inequality[J]. IEEE Transactions on Automatic Control, 1997, 42(2): 239-243. [6]Moon Y S, Park P, Kwon W H, et al. Delay-dependent robust stabilization of uncertain state-delayed systems[J]. Internation Journal of Control, 2004, 74(14): 1447-1455. [7]Wang Y, Pandharipande A, Polo Y. Distributed compressive wide-band spectrum sensing[C]. Information Theory and Application Workshop (ITA), San Diego, CA, 2009: 2337-2340. [8]Pudlewski S, Melodia T. On the performance of compressive video streaming for wireless multimedia sensor networks[C]. IEEE International Conference on Communication, Cape Town, 2010: 1-5. [9]Boumal N, Absil P A. RTRMC: A Riemannian trust-region method for low-rank matrix completion[C]. International Conference on Neural Information Processing Systems, 2011: 406-414. [10]Keshavan R H, Oh S, Montanari A. Matrix completion from a few entries[J]. IEEE International Symposium on Information Theory, 2009, 56(6): 324-328. [11]Lee K, Bresler Y. ADMiRA: Atomic decomposition for minimum rank approximation[M]. Wiley: IEEE Press, 2010: 4402-4416. [12]Haldar J P, Hernando D. Rank-constrained solutions to linear matrix equations using power factorization[J]. IEEE Signal Processing Letters, 2009, 16(7): 584-587. [13]Wen Z W, Yin W, Zhang Y. Solving a low-rank factorization model for matrix completion by a non-linear successive over-relaxation algorithm[J]. Mathematical Programming Computation, 2012, 4(4): 333-361. [14]Tanner J, Wei K. Low rank matrix completion by alternating steepest descent methods[J]. Applied and Computational Harmonic Analysis, 2016, 40(2): 417-429. [15]王萼芳, 石生明. 高等代数[M]. 北京: 高等教育出版社, 2003.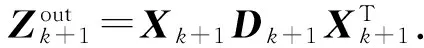
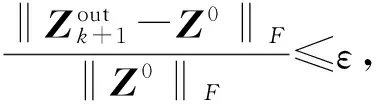
2 收敛性分析
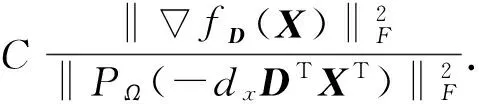
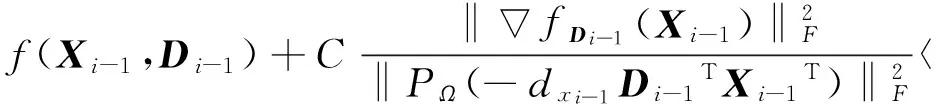

3 数值实验





4 结 论

