基于自适应模糊PID的无人机四维航迹控制研究

, , ,

(西北工业大学 自动化学院，西安 710129)

0 引言

随着无人机在军用和民用领域不断的发展，如何进一步提高无人机的自主控制能力以及执行任务的能力成了当前研究的一大热点。在一般的导航任务要求中，只需实现三维航迹的控制跟踪。许宗飞等[1]通过在平面导航基础上引入高度控制，实现了无人机的三维航迹控制，但航迹跟踪效果存在一定误差。杨格等[2]采用PID神经网络方法设计了高度控制器，用于无人机的三维航迹控制中，与传统的PID 控制相比，明显改善了控制器的性能，提高了三维航迹跟踪的精度，但是无法满足按时到达目标位置，实时侦测打击的任务要求。管军等[3]通过滑模变结构控制理论和反步控制理论设计的控制器，能较好的跟踪三维空间航迹，但时间控制精度不高。

本文首先设计了四维导航系统的总体结构图，给出了导航过程中航向角、高度以及速度的求解方法以及平面航迹控制、高度控制以及速度控制的具体实现方法。然后分别给出了基于自适应模糊PID的高度、速度控制器的结构图，详细介绍了模糊PID控制器的具体设计过程，最后将设计的控制器组成一个完整的飞控、导航系统，用来实现包括按时到达(时间维度)的无人机四维航迹控制。

1 四维导航系统结构设计

无人机四维航迹控制不仅包括平面航迹控制和高度航迹的控制，还对到达时间以及飞行速度提出了要求。导航系统是在飞控系统作为内环路的基础上设计的导航外环路，主要负责控制量的解算和自主飞行任务。

平面航迹控制：由无人机的位置和给定的航线，计算偏航距和航线角，通过设计控制律，计算需要的航向角控制量，将其给入到飞行控制系统，飞行控制系统根据设计的航向控制率，通过调整副翼和方向舵的偏转角度，从而达到对无人机水平面的航迹修正和控制。

高度航迹控制：根据程序中给定的航程点位置，导航系统将航点高度信息提取后，根据无人机当前的位置，通过数学计算方法实时给出无人机处于任意位置时所需的高度控制量，将其送入到飞控系统的高度控制器中，通过调节升降舵的偏转角来实现高度轨迹的实时跟踪[2]。

速度控制：由给定时间和无人机距目标点的水平距离实时计算无人机所需的飞行速度，将该速度作为控制量给入到飞行控制系统的速度控制器中，通过对发动机推力的控制来实现飞行速度的跟踪控制。

四维导航总体结构如图1 所示，其中包括飞机模型、飞行控制系统、传感器模块(包括无人机三维位置信息、速度信息等采集模块)和导航解算单元(包括航向控制量、速度、以及高度的控制量计算)。

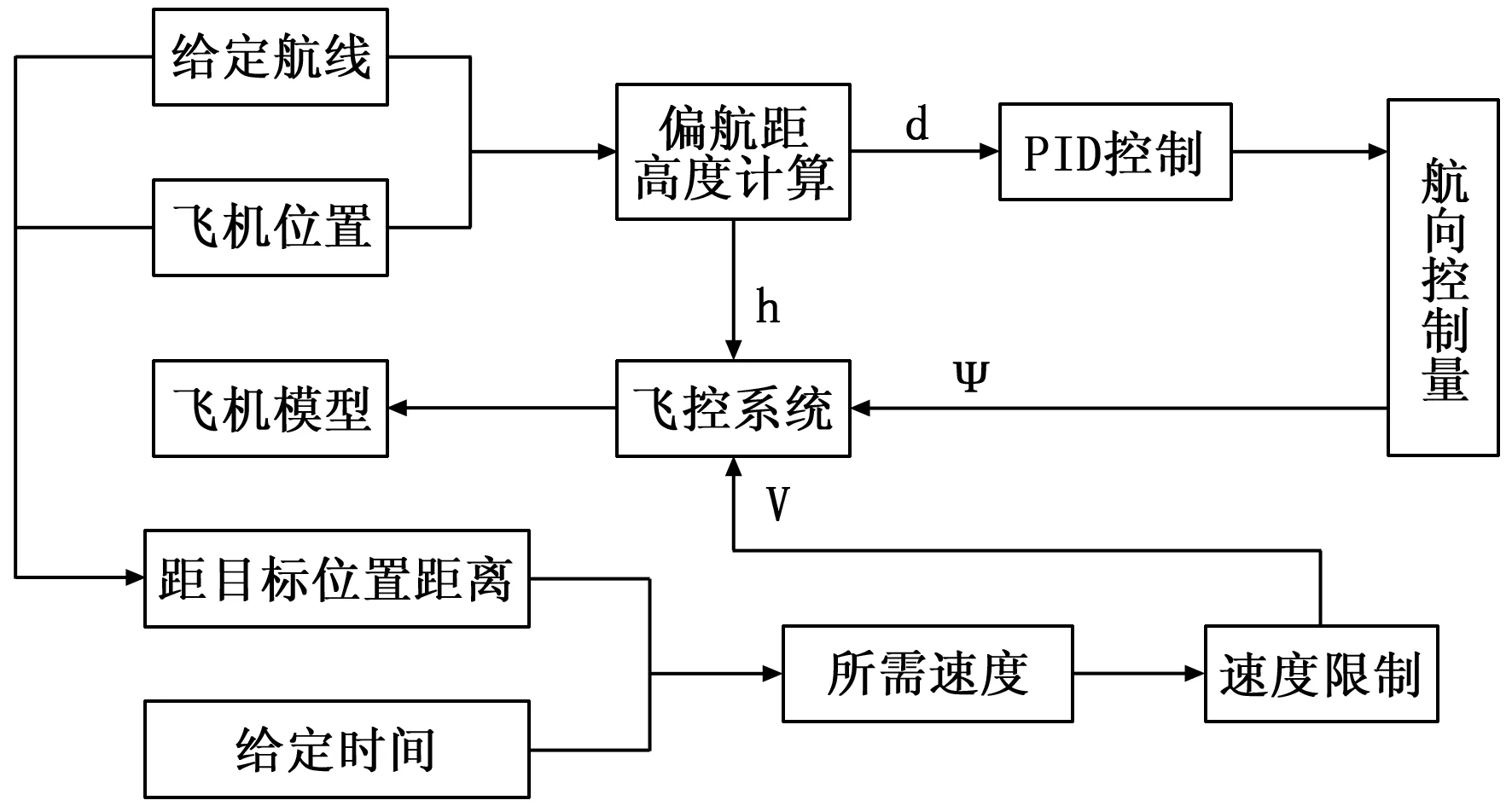
图1 无人机四维导航结构框图

2 高度控制器设计

由于无人机在进入自主导航时，所接收到的航线是离散的航程点，即只有航程点处的准确三维坐标，对于高度值而言，航程点之间的各点高度信息是未知的，为了实现准确的直线三维航迹跟踪，需要计算无人机任意位置对应的应飞高度，具体的高度计算方法参见文献[1]。

无人机的高度控制是实现三维航迹跟踪的基础，由于模糊控制是基于经验和知识的一种规则控制，在控制中可以对不精确的数学模型进行控制，且具有控制机制容易实现，过程简单的特点。将模糊控制理论应用到无人机的高度控制器设计中，作为无人机的纵向控制量，高度的控制需要通过俯仰角的变化进行调节，所以高度控制器的内回路为俯仰角控制回路，俯仰角控制仍然采用传统的PID控制[4]，其输出量作为升降舵偏的控制量。具体的高度控制结构如图 2 所示。

图2 基于自适应模糊PID的高度控制结构图

由导航系统计算出的高度控制量与传感器采集的无人机高度信号值，送入到高度控制器中，控制器的输出作为升降舵偏转角指令信号进行升降舵控制，从而实现无人机的高度控制。

3 速度控制器设计

无人机飞行速度的控制是在一般三维导航的基础上提出的更高的任务要求，由于要进行四维航迹控制，则需要实现无人机的速度控制以及速度控制量的计算。本文采用的发动机模型是通过控制风门开度来控制发动机推力，将速度控制器的输出量作为发动机的风门开度输入到发动机中，从而改变发动机的推力以达到速度控制的目的，考虑到模糊控制的优越性，将其应用到速度控制器的设计中，具体的速度控制器结构如图3所示。

图3 基于自适应模糊PID的速度控制结构图

根据发动机的特性，以及考虑到速度的快速响应，在进行速度的控制过程中，可使风门以较大的开度快速响应给定速度，当速度达到预定值后再自动调节，切换到小的开度。为保证发动机的正常工作，风门开度限制在10%～100%，即当速度控制器输出量小于10%时取风门开度为10%，当速度控制器输出量大于100%时取风门开度为100%。

速度控制量可以通过所剩航线的总长度和剩余航行时间的比值进行实时计算，将计算出的无人机所需速度给到速度控制器中进行速度控制。这样虽然能提高无人机的速度控制精度，但会使发动机的风门开度、推力值以及无人机的速度不断发生变化，这是工程上所不希望的。所以，本文中只在每次进行航程点切换时计算无人机的所需速度，在航线段上进行速度保持，当到达下一航线段再根据距离和时间的比值计算速度的给定量。且该无人机巡航速度范围为35～55 m/s。当计算出的速度大于55 m/s时，取速度为55 m/s，当计算出的速度小于35 m/s时，取速度为35 m/s。

速度控制的过程为：根据传感器采集的无人机速度与导航系统通过以上方法计算出的速度控制量，送入到速度控制器中，用经过模糊PID控制器后的输出量调节发动机风门开度的大小，最后通过发动机推力值的变化，实现无人机的速度控制。

左圆最大的建筑是喷泉，直径十多米的水池镶着马赛克，池子里用水泥钢筋搭建的假山，因多年不用，成了鸟儿们的乐园。有意的是假山上面雕塑着的那几只海鸥。有的平静地飞翔，有的欲飞欲止，最上面的那只折了一个膀的海鸥，看样子是凯旋归来？又像是在花样飞翔？让人浮想联翩……

4 自适应模糊PID控制器设计

根据以上两节设计的高度、速度控制器的结构，本文的模糊PID控制器设定为二输入，三输出的形式。以速度、高度的偏差e和偏差变化率ec为系统输入量，PID 参数的修正值ΔKP，ΔKI，ΔKD为系统输出量。最终控制器的控制量参数为PID控制器的初始值与PID参数的修正值之和，自适应模糊 PID 控制器的结构框图如图4所示。

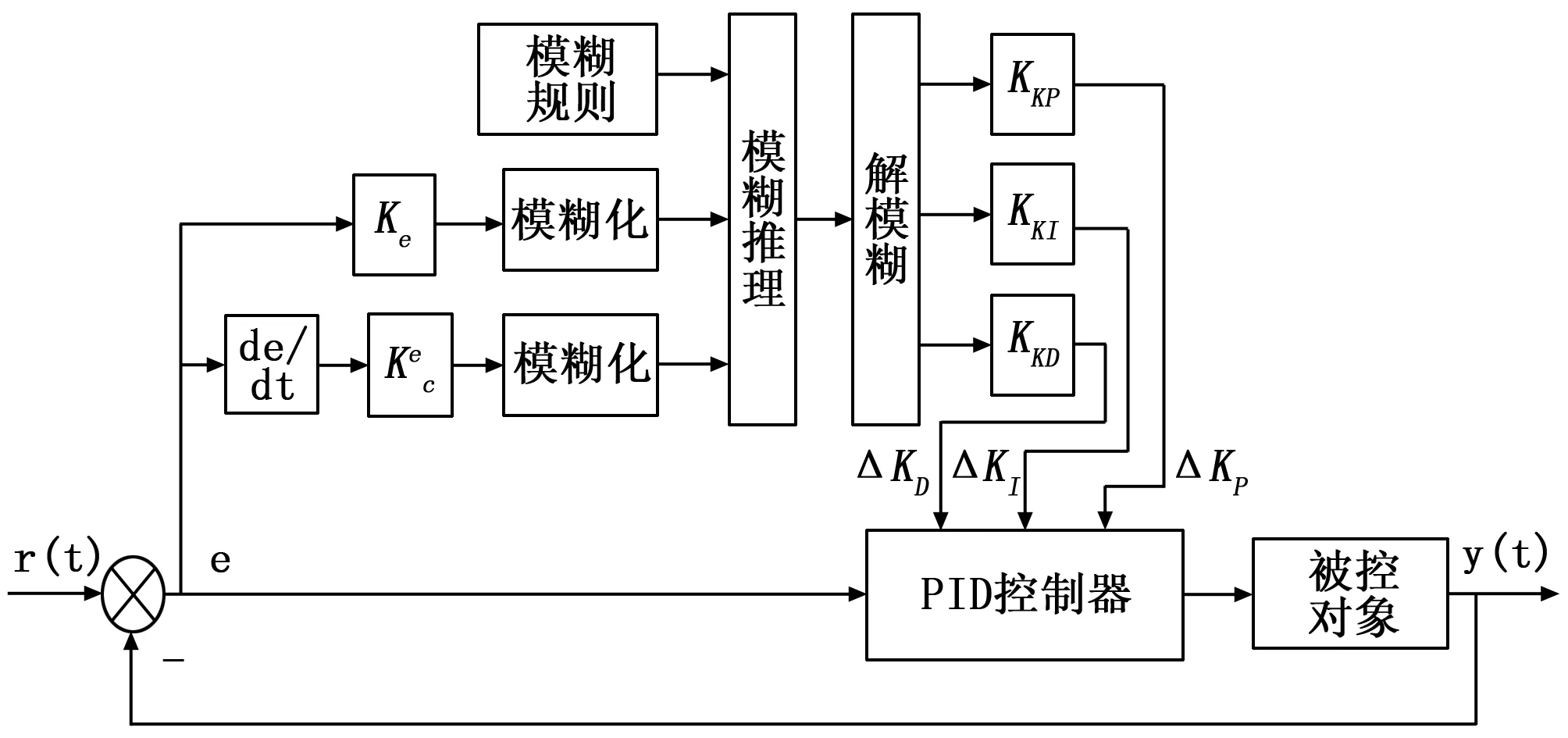
图4 自适应模糊PID控制器结构框图

语言变量：e，ec，ΔKP，ΔKI，ΔKD。

模糊子集：均为[ NB NM NS ZO PS PM PB ]。

基本论域和模糊论域：ec的论域取[-5,5]，其它变量的论域取[-6,6]。在进行模糊处理时，需要将基本论域转换到模糊论域，这就需要e、ec的输入量化因子Ke、Kec及输出变换比例因子KKP、KKI、KKD的调节，来实现论域的转换。

各个变量的隶属度函数均选为三角型。

4.1 模糊规则建立

自适应模糊 PID 控制器就是根据控制经验和实际调节过程中参数和控制效果的关系，建立一组控制规则，使其尽可能的满足在不同输入下，都能对应较好的控制参数和控制效果，而不同于传统的PID控制，在整个控制过程中控制律参数是不断进行自调整的[5]。使用模糊控制首先需要确定不同的偏差e和偏差变化率ec对应的调节方式，将其作为一组经验值设计成规则表，在控制过程中，由于e和ec是不断变化的，这就需要查表确定需要的输出量作为PID的修正量，对PID控制参数进行实时调节。

根据无人机控制系统调节过程中的参数变化趋势，以及控制经验知，控制过程中参数KP，KI，KD的取值变化如下[6-7]：

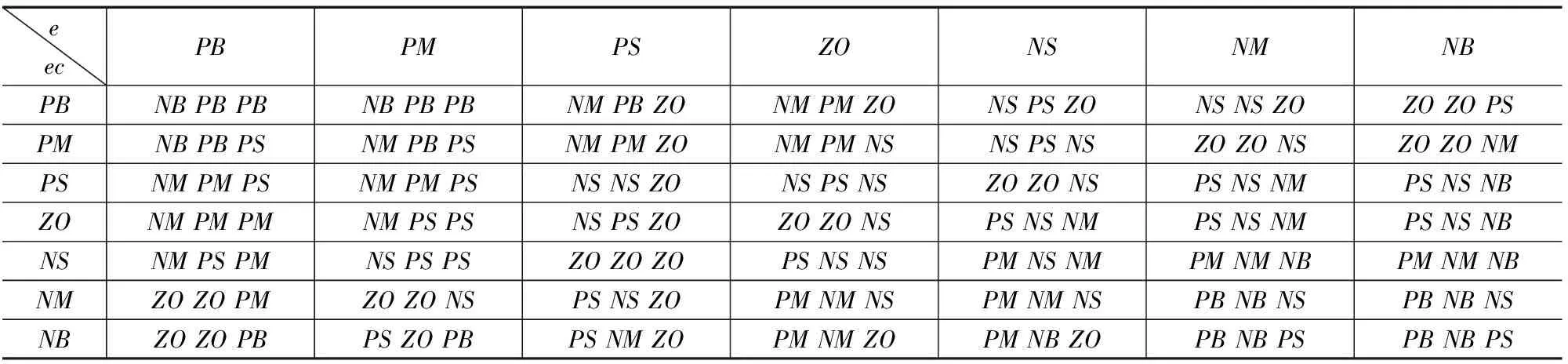
表1 ΔKP,ΔKI,ΔKD模糊规则表

注: 表 1 每格里有 3 个模糊控制规则，从左到右分别为ΔKP,ΔKI,ΔKD的模糊控制规则

1)当e较大时，需要较大的KP和较小的KD使控制器输出较大值，快速跟踪控制量，减小偏差，这种情况下一般令KI=0，用来防止积分饱和。当e较小时，KI的值需要适当增加，以减小系统的静态误差，同时取适当的KD以改善系统的动态特性；

2)当e和ec处于中等大小时，KP取值应减小，KI取值增加以减小系统超调量，KD的取值要适中以提高系统的响应速度；

3) 当ec较大时，应取较小的KP以减小超调，取较小的KD来减小调节时间，以及较大的KI。当ec较小时，一般取较大的KP和KD，较小的KI；

根据以上的分析以及对飞控系统控制器参数调节的经验，制定出如表1所示的模糊规则。

4.2 解模糊

在建立了模糊规则后，不同的输入量经过模糊规则处理后，输出的变量是一个不能直接当作控制量进行处理的模糊集，即为了得到实际的控制量，必须经过一定的方式进行处理，将其转化为控制系统能识别的数字量，进而计算控制器的实际参数。这种解模糊过程的处理方法有多种，本文中采用加权平均法对模糊量进行处理，具体的解模糊化过程参考文献[8]。

经过解模糊处理后得到的输出量即为PID参数的修正量，最后的PID参数调整值为PID控制器的初始值与模糊控制器输出的修正值之和。

5 仿真与分析

根据无人机风洞实验数据，进行无人机系统建模，根据四维航迹控制结构图以及第2、3节中的高度和速度控制器结构图，在Matlab/Simulink仿真环境下，分别设计包括传统PID的航向控制器、自适应模糊PID的无人机高度和速度控制器的飞行控制系统以及包括导航数据解算的导航系统。其中高度控制器中的PID参数分别为：比例KP=0.8,积分KI=0.08,微分KD=0.5，输入量化因子Ke=0.005,Kec=0.5,输出比例因子KKP、KKI、KKD均为1。速度控制器中的PID参数分别为：比例KP=0.8,KI=0.08,KD=0.5，输入量化因子Ke=0.25,Kec=0.01，输出比例因子为KKP=0.5、KKI=1、KKD=0.5。

将设计好的飞控/导航系统应用到四维航迹控制中，给定的航程点如下：(0, 0, 0)，(10 000, 0, 1 000)，(15 000, 0,1 000)，(15 000, 10 000, 1 500)，(15 000, 15 000, 1 500) (10 000, 20 000, 2 000)，(5 000, 25 000, 2 000)，(-10 000, 25 000, 1 500)，(-15 000, 25 000, 1 500)，(-15 000, 18 000, 1 000)，(-15 000, 15 000, 1 000)，(-7 000, 11 000, 500)，(-3 000, 9 000, 500)，规定沿航线到达最后一个航点的时间为1 800 s。到达目标航点后程序停止运行，初始时间为0 s，初始无人机速度为35 m/s，初始高度为0 m，初始航向角为0°。仿真结果图如下：

图5 无人机三维航迹仿真曲线

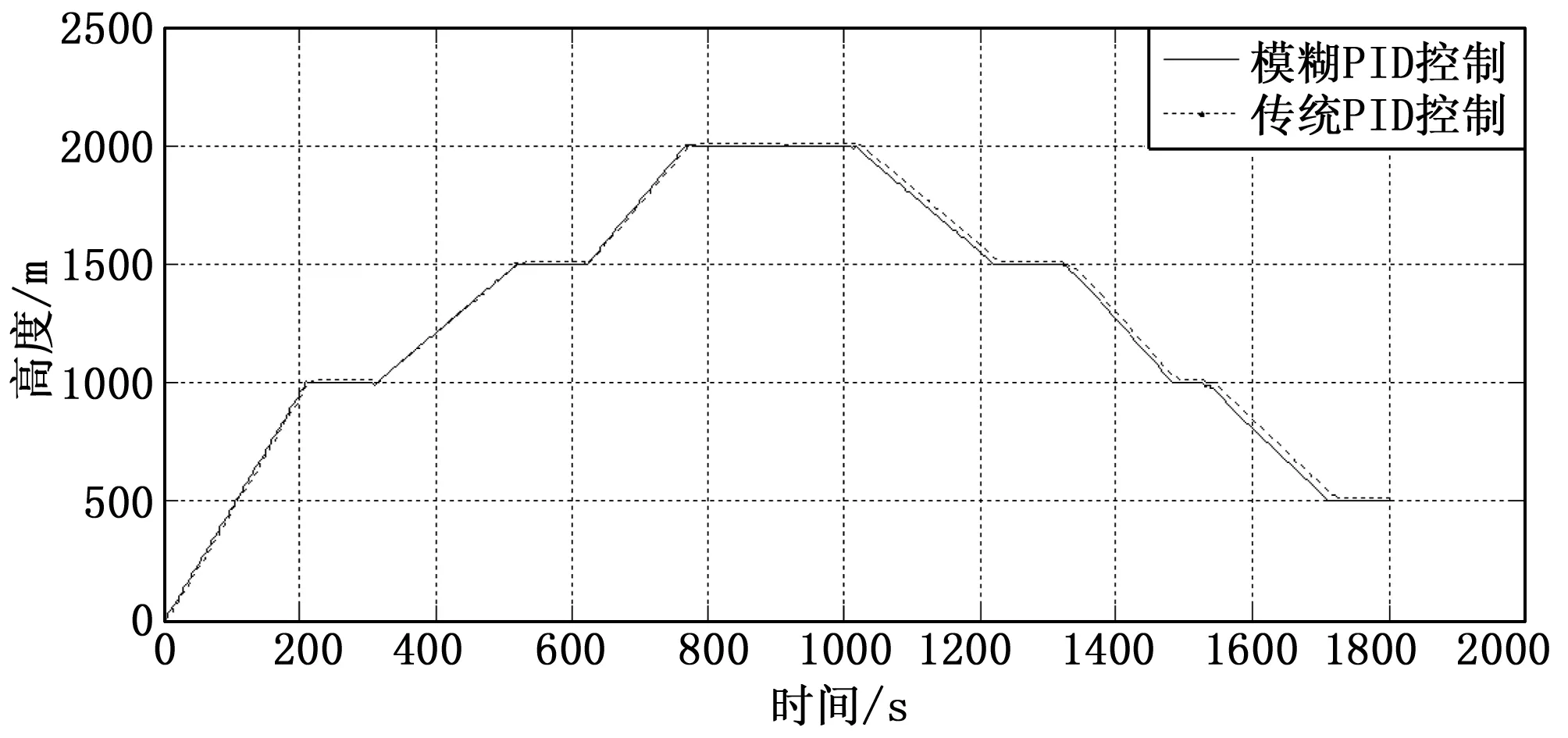
图6 无人机高度仿真曲线

图7 无人机飞行速度仿真曲线

图8 发动机风门开度仿真曲线

由图5可知，无人机从起点出发，经过各个航程点，最后到达目标点位置，两种控制器在一定程度上都能满足三维航迹跟踪的要求，但使用自适应模糊PID控制器的飞控、导航系统，具有较小的偏航距，很好的实现了航迹的跟踪，且在转弯时的掉高控制过程调节时间更短。从图6中可知，采用一般的PID控制器进行高度控制时，存在10 m左右的稳态误差，而通过模糊PID的自适应参数调节，很好地消除了系统的稳定误差，且系统的响应速度也有所提高。

为了直观的显示速度的响应曲线，将纵坐标从46 m/s开始(无人机初始速度为35 m/s)。如图7所示，当无人机到达最后航程点时，两种控制器用时均约为1 805 s，时间控制误差为1 min/6h，满足时间的控制精度。但明显可以看出当航线进行切换时，传统PID的速度控制图像存在较大的波动，且响应时间长。而模糊PID控制的速度图像存在速度波动小，响应快，超调量小的优点，这也是工程中所希望的，而且根据3中给出的速度计算方法可知，只在每次切换航线段时速度发生变化，在该航线上速度保持不变，当到达下一航线段再根据距离和时间的比值计算该航线段的速度，再进行速度控制，程序中给定的航程点共13个，即有12段航线，就会有12次的速度变化，这刚好对应速度图像中的12段速度值不同的曲线段。由图8可知，每当速度进行切换时，通过自动油门系统调节风门的开度，风门开度的快速变化可以使得发动机的推力快速响应速度控制量，从而实现速度的控制，由图可知模糊PID控制器的风门开度变化更快，调节范围更大，这也对应其速度的快速响应。

从图5～图8可知，用基于自适应模糊PID控制设计的高度、速度控制器进行无人机四维航迹控制，结果具有控制超调量小、调节过程平稳、稳态误差小等优点，不仅能实现很好的三维航迹跟踪效果，而且能很大程度的提高速度控制的响应时间和稳定性，使时间的控制误差为1 min/6h，很好的实现了四维航迹的跟踪控制。

6 结论

经过仿真分析表明：与传统的PID控制相比较，基于自适应模糊PID控制设计的高度和速度控制器具有超调量小、调节过程平稳、稳态误差小的优点，能满足无人机四维航迹控制的飞行要求。

[1] 许宗飞,袁冬莉,刘小俊,等. 小型无人机三维导航控制研究[J]. 计算机测量与控制,2010(4):827-829.

[2] 杨 格,闫建国. 基于PID神经网络的无人机三维航迹控制方法研究[J]. 现代电子技术,2014(8):46-50.

[3] 管 军,易文俊,常思江,等. 某型无人机三维空间航迹跟踪控制方法研究[J]. 兵工学报,2016(1):64-70.

[4] 王 健,王承龙,李 智,等. 基于自适应模糊PID的四旋翼飞行器悬停控制[J]. 桂林电子科技大学学报,2016(5):406-411.

[5] 王 博,陈万强,李祥阳. 基于模糊自适应PID控制的舵机系统仿真研究[J]. 重庆理工大学学报(自然科学),2015(10):52-56.

[6] Zhang Dizhou, Chen Zili, Xi Leiping. Adaptive dual fuzzy PID control method for longitudinal attitude control of tail-sitter UAV[A]. International Conference on Automation and Computing[C]. 2016:378-382.

[7] 吴 玲,闻 凯,董 敏,等. 自适应模糊PID控制在汽车ABS系统中的应用[J]. 自动化技术与应用,2016(1):26-31.

[8] 崔家山. 基于自适应模糊PID的飞航导弹控制系统设计[D].哈尔滨:哈尔滨理工大学, 2012.