基于ANFIS的振动筛控制系统设计

， ，，

(湖北大学 计算机与信息工程学院，武汉 430062)

0 引言

在矿石破碎筛分流程中，振动筛的的好坏直接关系到生产线的产量和成品品质。因此我们要选择质量可靠、处理量大的筛分设备，在正常运行前应将其振动频率和倾角进行调试。目前，筛分领域市场振动筛的振动频率和倾角主要依赖于操作人员的经验，而当矿浆粒度和浓度发生变化时，人工操作就会产生滞后，参数难以达到最佳状态，降低了筛分效率。模糊控制可以模拟人类的实际经验判断生产状况，辅以神经网络的自主学习能力便可实现振动频率与倾角的自动调节。本文将自适应神经模糊推理系统(ANFIS)应用于振动筛的控制，大大加强了系统的自适应能力，提高了生产效率。

1 振动筛工艺流程

振动筛是一种适用于细粒物料的湿式分级与固液分离的选矿设备，主要用在稀有、有色和黑色金属矿山、非金属矿山等领域。振动筛工作时，矿石经破碎机破碎后与水混合成流体进入振动筛，通过两电机同步反向旋转使激振器产生反向激振力使得物料随筛体带动筛网做纵向运而周期性向前抛出一个射程，从而完成矿料筛分作业，得到合格的筛下物料。

振动筛通过调节变频器的电流来改变振动筛的振动频率,达到调节振动筛振动频率的目的；通过改变伺服电流来控制筛机固定架后作支撑用的升降装置的左右两个丝杆升降机，从而实现对筛机倾角的控制。由于振动筛的生产效率和振动频率呈指数关系，生产效率随着振动频率的增加而迅速增加，能够有效避免堵塞网眼的现象。但是如果振动频率过大会加大振动电机转轴两端偏心块的摩擦导致电机损坏。除此之外虽然筛面倾角越大，其处理量越大，但筛分效率会下降，因此需要合理调整频率和倾角。

工作人员通过外部传感器检测到进料矿浆的粒度及浓度，根据进出料参数来调整筛机的工作倾角及振动频率，使筛网的处理效率及处理质量达到最佳，以获得最大筛分效率。PC机上的数据处理软件将数据实时或筛选后保存于数据库；如此反复模拟生产实际情况，得到大量的原始数据并保存到数据库，通过开发的大数据分析处理软件得出最佳工作倾角及振动频率参数与粒度及浓度之间的关系，将其拟合为数学函数曲线并写入控制程序，再次进行反复的模拟试验对拟合的数据进行验证，直至验证与原试验数据吻合。如图1所示。

2 系统的整体设计

该系统分为五大部分：数据采集部分、振动筛频率控制部分、倾角控制部分、控制信号I/O部分以及人机界面部分。试验数据经外部传感器进入采集板并通过TCP/IP端口协议与PLC控制器进行通讯，PLC实时返回相应的数据信息并保存到PC机的数据库中。利用大数据处理软件对数据进行分析筛选得到最佳频率与角度数据组以供模糊神经网络进行学习训练。

设备的状态通过S7-200PLC的DI输入检测，倾角通过PLC的高速计数输入检测，粒度及浓度经外部传感器传递给PLC的AI接口，通过嵌入PLC的模糊神经网络算法计算出调节振动筛频率和倾角的信号，该信号经D/A转换传入PLC自带的RS485接口来改变变频速率以及伺服电机的电流，从而实现了自动调节振动筛频率及倾角的功能。PC机上开发设备操作及数据采集记录程序实现试验所需功能；开发大数据分析处理软件，依据筛分效率和处理量计算公式，得出最佳倾角及振动频率参数与粒度及浓度之间的关系。如图2。

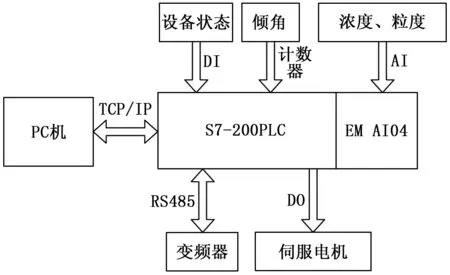
图2 控制系统硬件结构图

2.1 ANFIS结构与原理

ANFIS是MATLAB自带的一种模糊推理系统,可以将现场实际获得的输入输出数据作为训练样本，是模糊推理系统能够“学习”到从输入映射到输出之间的规律，从而在系统内部建立起实际应用的模糊规则。网络首先将输入量载入进行数据的正向传播。第一层有2个神经元作为网络的输入清晰量；第二层神经元是将输入的清晰量量化为模糊语言量，计算各输入量的隶属度并同时划分出模糊子集；第三层神经元是将量化后的模糊量进行规则匹配，神经元节点内部执行“与”运算；第四层神经元将根据第三层网络的规则匹配的结果计算每条规则的激活度；第五层神经元将根据加权平均法对输出的模糊语言量一一进行清晰化。数据正向传播完成后得到的实际信号将于事先给予的导师信号作比较，根据比较后得到的差值按照负梯度方向反向修改网络的参数，此时网络为反向传播。

本文的ANFIS结构采用5层前馈网络结合T-S模糊推理模型，根据筛选出的输入-输出数据进行结构、参数的辨识，从而建立相应的模糊规则及调整网络隶属度函数的参数。该控制模型的输出量是输入变量的线性函数。整个模糊神经网络结构为5层，包括：输入层、隶属度函数层、模糊规则层、模糊判决层和输出层。如图3。

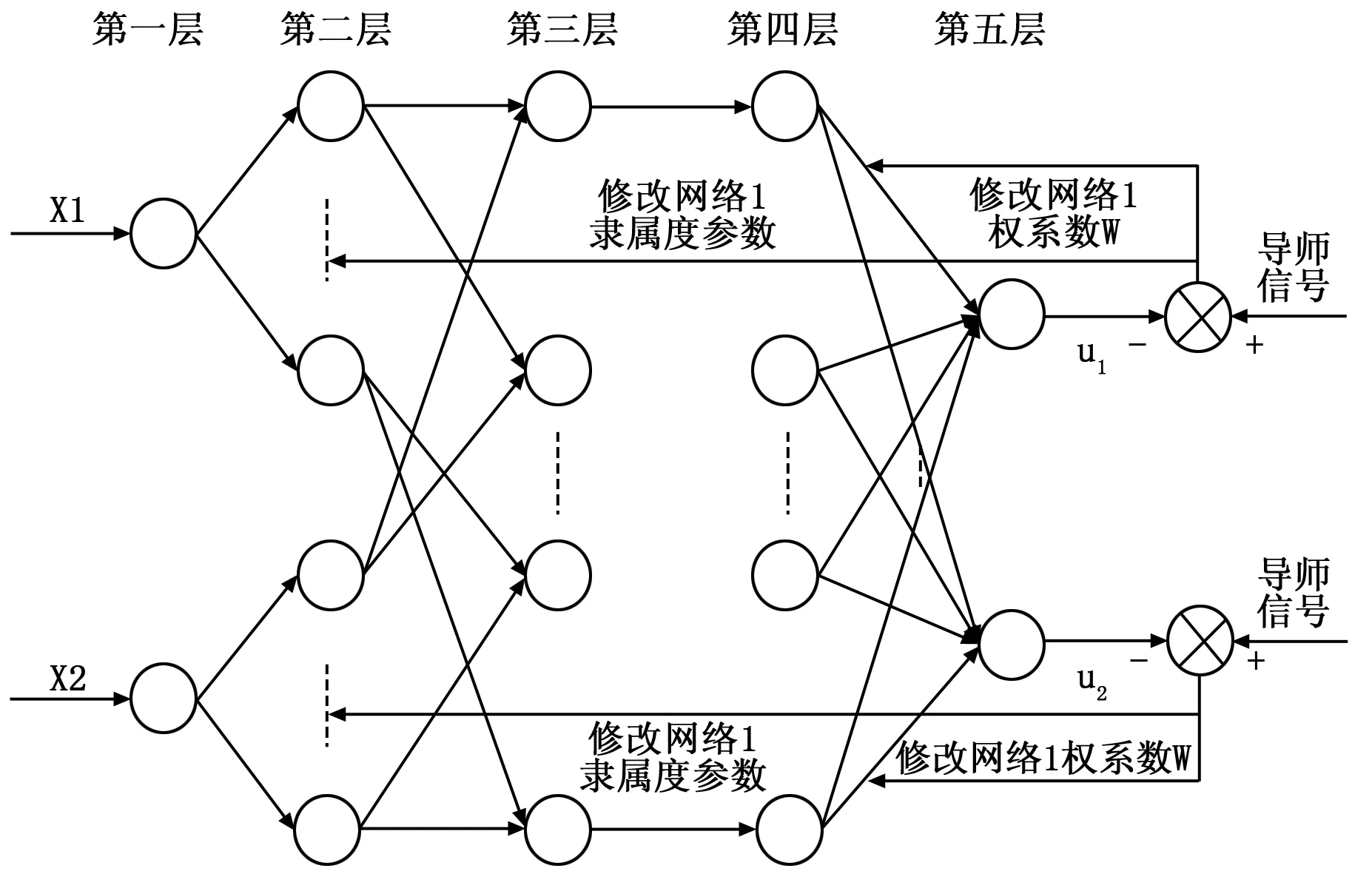
图3 模糊神经网络结构图

2.2 网络构成原理

第一层是输入层，需要完成接收粒度与浓度参数并将其传递到下一层的功能，该系统有2个输入量即节点数i等于2，x1为矿料粒度的参数，x2为浓度的参数。第一层输出与输入的关系为：

(1)

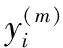
第二层是隶属度函数层，本层需要完成输入量模糊化的功能，两个输入量均采用高斯型隶属度函数，将每个输入量的基本论域划分为4个模糊子集：{NS,ZO,PS,PL}，对应的模糊语言量为{稍小，不变，稍大，极大}。第二层节点数k等于模糊子集数，而隶属度函数的形状会在样本训练结束后有一定地改变。1,2层之间的权系数为1，第二层输入为：

宝宝贫血一般都是缺铁性贫血，需要补铁。但是妈妈们要注意生理性贫血是正常的，无须任何治疗和补铁。宝宝出生时血红蛋白高达 190 g/L,然后逐渐下降，2个月之后，宝宝的骨髓造红细胞的功能才开始活跃。在2～3个月的时候为 90～110g/L，早产儿在3～6周的时候可以低到70～90g/L，这些都是正常的。

(2)

第二层输出与输入关系为：

(3)

第三、四层是模糊推理层，本层需要完成建立模糊规则及模糊规则匹配的功能。第三层根据推理规则产生前件的适合度，计算模糊规则的激励强度；第四层产生推理结果，完成各条规则适合度的归一化计算。因此第三层节点数j等于模糊规则数，节点内部执行“AND”运算。第四层完成规则后件且节点数等于第三层的数目j，计算出建立的每条规则的激活度。第二层和三、四层之间的权系数为1,其输入输出关系为:

(4)

(5)

第五层是输出层，本层需要完成将模糊量转化为精确量的功能。每个神经元节点代表着一个输出量即节点数为2。由于本文采用的模糊推理模型为Sugeno型，其输出函数为输入函数的线性函数，Wj表示最后输出各规则在总输出中所占的权重。采用加权平均法去模糊化。加权平均法是将输出量模糊集合中所有元素进行加权平均作为输出量执行，即输入乘以相应隶属度的累加和与各隶属度累加和的比值。如下式：

f=Ax1+Bx2+C

(6)

(7)

其中：f是模糊输出函数，A、B、C为该函数的学习参数。

2.3 参数学习

该网络采用BP学习算法，首先对隶属度函数的2个参数和4、5层网络之间的权系数进行初始化，然后根据教师信号与实际输出相比较得到的误差信号来修改隐层网络的各参数。误差公式为：

(8)

式中，xi为导师信号即期望信号，y(5)为网络控制器的实际输出，BP算法按误差J的负梯度方向修改神经网络的权系数和隶属度函数中的参数，经过多次训练使得误差J的取值小于设定值。则4,5层权系数Wj及隶属度函数参数的学习公式为：

(9)

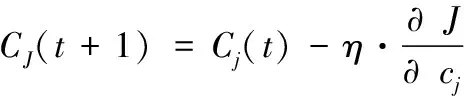
(10)

(11)

3 MATLAB试验仿真

将振动筛的不同状态输入数据作为离散点，根据振动筛最大筛分效率的公式，分别将每个离散点代入公式计算得到此输入状态下的最佳振动频率和倾角的输出，然后将对应的输入输出点存入数据库作为备选的训练样本，并将训练样本嵌入自适应模糊神经推理系统用作训练控制器的参数，从而得到控制器的控制规律。由于MATLAB的自适应模糊推理系统只能完成多输入-输出的结构，因此需要分别根据不同的输出量进行仿真，最后得到振动频率和倾角的绚丽按误差-训练次数的曲线。

3.1 基于ANFIS的系统建模

1)数据的载入 以DZSF-520型高频振动细筛筛分赤铁矿为例，通过现场试验台采集大量数据，从中筛选出14组数据作为网络的样本。如表1所示。赤铁矿的粒度x1(mm)和浓度x2(%)为网络的学习输入，振动筛的最佳频率y1(赫兹)和倾角y2(度)为网络的输出，每个输入、输出量有3个隶属度。由于该模型为多输入多输出模型，而ANFIS只能提供多输入单输出模型的仿真，因此本文将两个不同的输出分别进行仿真。将筛选出的14组数据作为训练样本，后5组作为测试样本，然后利用ANFIS编辑器数据载入MATLAB工作空间。如图4。

2)生成初始FIS 用ANFIS构造FIS时必须有一个初始的FIS结构，ANFIS在此基础之上才能根据已有的数据修改模糊结构直至该结构符合要求。本文采用相减聚类法(Genfis2函数)自动生成模糊推理系统的初始FIS。

表1 训练样本数据表

图4 ANFIS数据载入界面

3)网络的学习训练 采用backpropa方法训练网络，从而建立了与网络输入输出相适应的模糊规则(T-S型模糊模型的输出为输入的线性函数)，训练结束后可以看到隶属度函数的形状发生了变化，这是由输入输出数据所决定的。图5为训练结束后得到的输入隶属度函数，图6分别为系统振动频率和倾角输出的模糊规则观测窗。

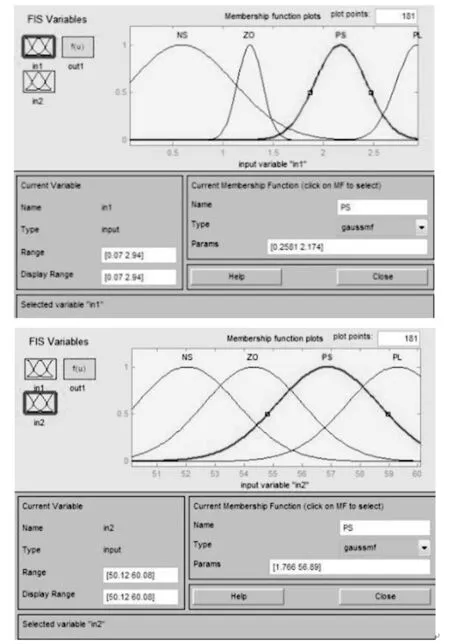
图5 训练后的输入隶属度函数

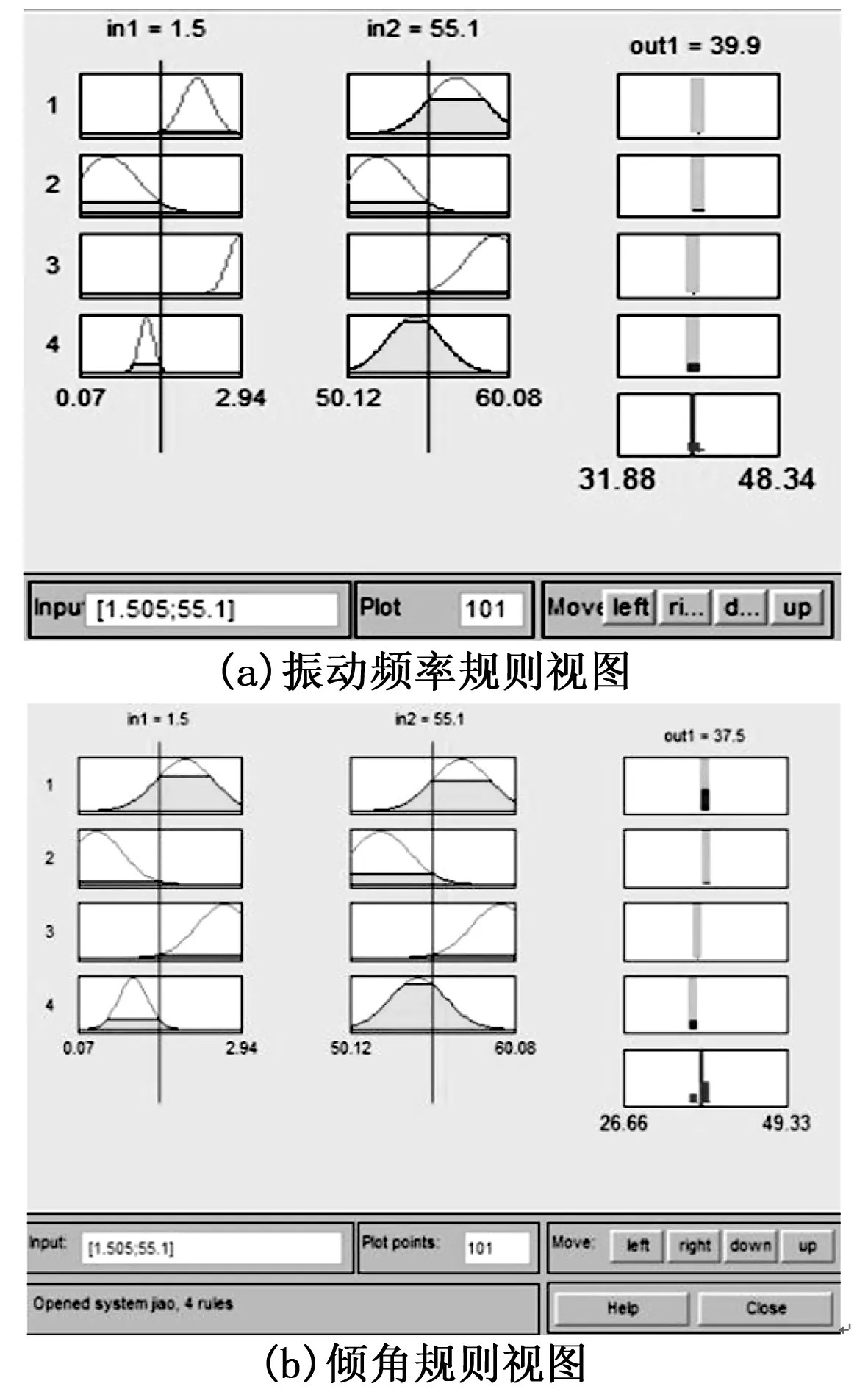
图6 模糊规则观测窗

将网络目标输出与实际输出作差得到均方差E，判断误差E是否小于0.05，若不满足条件，则加大训练次数直至满足要求，最后得到的误差-训练次数关系图如图7。从图中可以看出：网络经过150次训练后的输出振动频率训练误差为0.046564，输出倾角的训练误差为0.0084107。

从图7可以看出，振动筛的振动频率和倾角的输出的训练误差较小好且具有较快的收敛速度，能够满足要求。

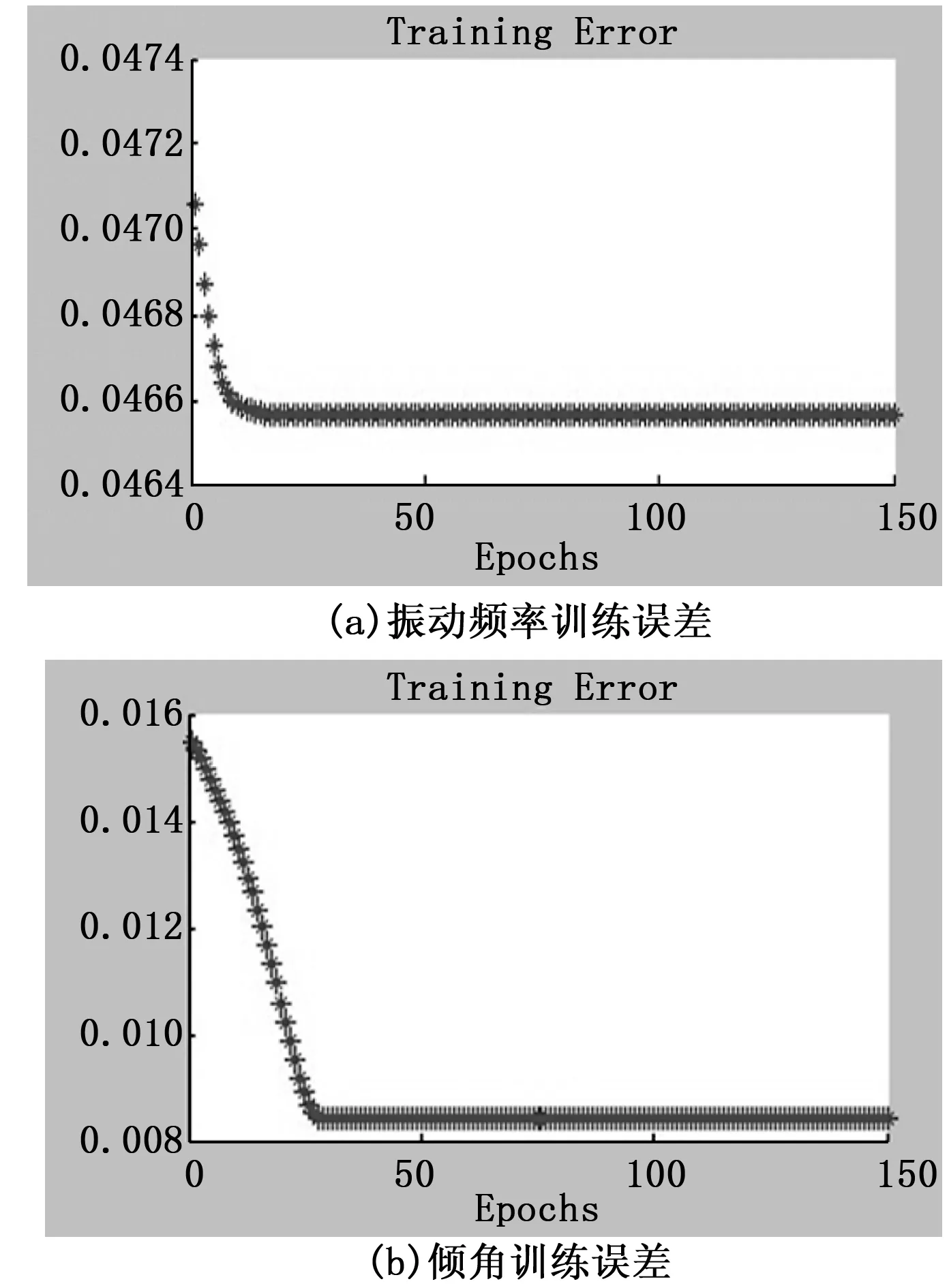
图7 训练误差-训练次数关系曲线

3.2 模糊推理数据表

根据图5所示模糊规则观测窗的显示内容可知：当输入量粒度x1=1.5，浓度x2=55.1时，相应的输出量振动频率y1=39.9，倾角y2=37.5。因此可以拖动观测窗上的游标线得到表2，与现场采集到的数据表1内容基本吻合，这表明模糊神经网络算法在振动筛输入输出量自动调节过程当中的应用史可行的。

4 结束语

本文将自适应模糊控制算法应用于振动筛工艺智能化控制系统，使得模糊系统更具灵活性，弥补了由于模糊控制系统过于依赖专家经验而导致的经验之外的失误。这样可以减少甚至消除现场使用时的工艺试验，不依靠操作者的经验积累就能使振动筛达到既定的使用效果和设备的处理能力,提高了筛网的筛分效率。仿真结果表明：利用模糊神经网络算法可以获得最佳参数，从而实现振动筛控制系统频率和角度的自动调节,因此该算法具有一定的应用前景。

[1] 陈 洋，吴怀宇.基于ANFIS的焦炉火道温度预报模型研究[J].计算机测量与控制，2007,15(2):462-464.

[2] 王 冷.基于模糊神经网络信息融合的采煤机煤岩识别系统[J].现代电子技术，2015(12)：38.

[3] 席爱民.模糊控制技术[M].西安：西安电子科技大学出版社，2010.

[4] 石辛民，郝整清.模糊控制及其MATLAB仿真[M].北京：清华大学出版社，北京交通大学出版社，2008.

[5] 秦 海,刘清平.基于ANFIS的汽车主动悬架仿真[J].农机化研究，2007(12)：55-58.

[6] 吴江燎，易灵芝.开关磁阻电机自适应模糊神经网络系统无位置传感器控制[J].煤炭学报，2010(8):35.

[7] 刘 鸣，张宝钢.基于ANFIS的蓄冷系统模糊控制设计[J].沈阳建筑大学学报(自然科学版)，2010(3):26.