基于网络分析的城区中小学服务区划分方法及其推广

李明轩 西北大学附属中学

中小学是满足居民基本生活需求的重要城市公共服务设施。面对中心城区建设用地相对紧张的窘境，如何结合实际情况合理划分中小学的服务范围具有重要的现实意义和理论价值。本文现以某市中心城区为例，对基于网络分析的城区中小学服务区划分方法进行演示。

1 研究区域情况

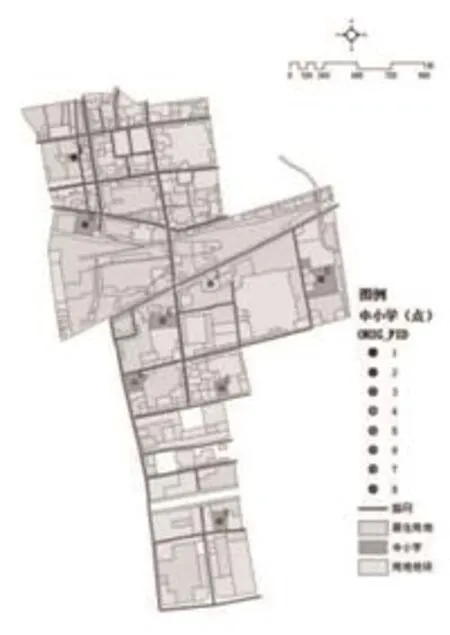
图1 中小学现状

研究区域位于某市市中心城区，区域呈长条状，南北长约2.2公里，东西宽约0.9公里，是该市城市总体规划确定的北部商住组团。研究区域内现状用地以居住小区和商业设施为主，其中，居住用地占建设用地的比例为37.11%，商业用地占建设用地的比例为25.93%，公共管理与公共服务设施用地占建设用地的比例为17.48%。研究范围内共有8所中小学，道路情况和居住情况如下（图1）。

2 研究方法选择

第一种方法：传统缓冲区法，即单纯按照国家标准规定的500m服务半径划分学区。该方法相对粗糙，会造成学区重叠或无法全覆盖（图2（1））。老城区人口密度高，能够用于建设中小学的城市建设用地十分紧张，因此，传统缓冲区法的实用性不强。

第二种方法：泰森多边形法，即按照学生住所到学校的最短直线距离划分中小学的服务范围，优点是无缝衔接，不会产生重叠或缝隙，能够避免传统缓冲区法的缺陷。该方法的缺点在于计算依据是直线距离，与实际道路存在显著差异，因此误差较大（图2（2））。

第三种方法：网络分析法，即基于地理信息系统（GIS）建立实际道路网络模型，按照学生住所到学校的最短实际距离的划分中小学的服务范围。与泰森多边形法相比，网络分析方法的最大改进在于计算依据由直线距离变为实际距离，优点是更加符合实际交通出行状况，精度更高。网络分析法的理论探讨和实践应用逐渐增多，技术路线现在也已经相对成熟。本文研究方法采用网络分析法。

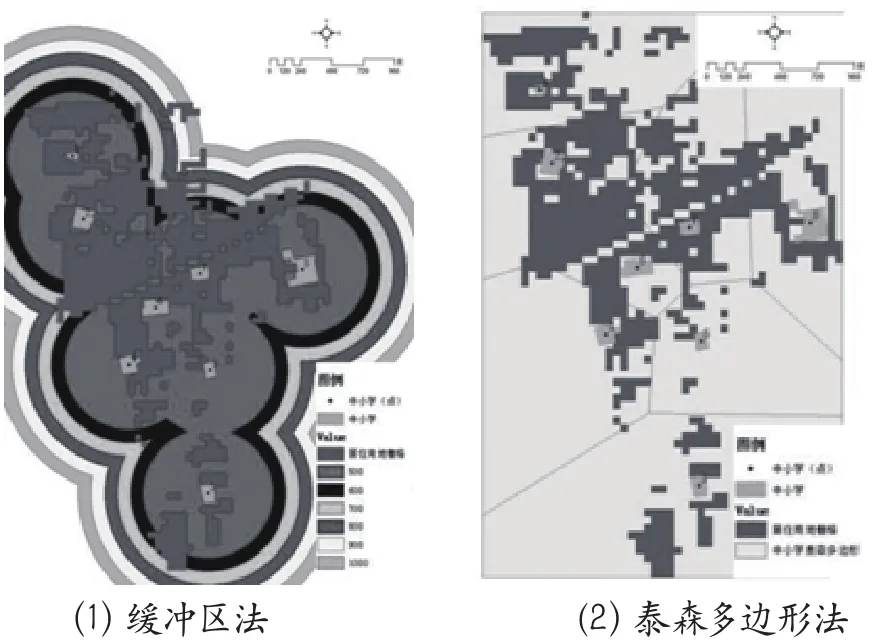
图2 学校服务区划分方法

3 基础数据处理

3.1 道路网络数据处理

在此，首先应该建立网络分析法需要的基础网络。中小学生从住所到学校的出行是依托城市道路系统，出行距离长短是本研究分析的重点问题。建立基础网络时应当以现有城市道路作为网络数据基础，道路的信息中包含长度属性。

3.2 学生住所数据处理

网络分析法的数据格式必须是点状要素，但是学生住所数据的格式是面状要素，因此，必须对学生住所数据进行格式转换，变为点状要素。首先，使用栅格方法平均划分居住用地，对学生住所进行逻辑抽象。理想状态下（即在居住密度一定的情况下），学生数量和居住面积是成正比的。以50m为边长把居住用地平均划分为一定数量的小栅格（正方形），每个栅格代表一定数量的学生。这样，学生住所之间的距离与用地现有住宅之间的距离相近，接近实际情况。其次，将栅格转化为点。点和栅格之间具有一一对应的关系。经过上述两个步骤后，共计产生面状栅格和点状要素两个图层，其中，栅格和点的数量均为829个，一一对应（图3（1））。

4 计算住所到学校的最短距离

使用GIS网络分析功能模块的最近服务设施计算方法，输入学生住所数据点状要素和学校位置点状要素，分别计算出每个学生住所数据点状要素对应的中小学，两者之间的出行距离是最短的。具体数据格式是路径，共计829条，每条路径包含路径编号、学生住所数据点状要素及所属小学编号等属性数据。（图3（2））

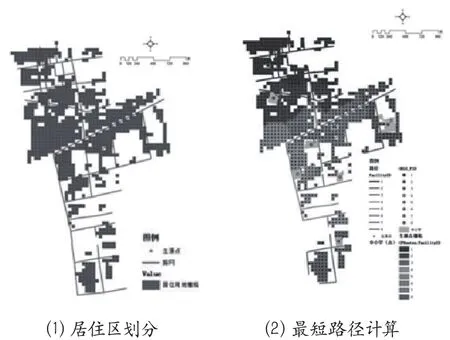
图3 居住区划分及最短路径计算

5 划分学校的服务范围

由于住所数据点状要素编号和居住地块栅格编号具有一一对应关系，同时，住所数据点状要素编号与路径数据编号（包含所属中小学编号）也具有一一对应关系，因此就可以将居住地块栅格编号与所属中小学编号连接起来。

通过属性查询计算可得到每个学校服务的居住地块栅格数，乘以每个栅格的面积2500平方米（50米*50米）。例如，编号为1的学校对应的栅格数为154个，服务的居住用地面积385000平方米。如果能够获得单位居住用地面积上的学生密度，就可以计算学校的学生规划，明确学校的建设标准。

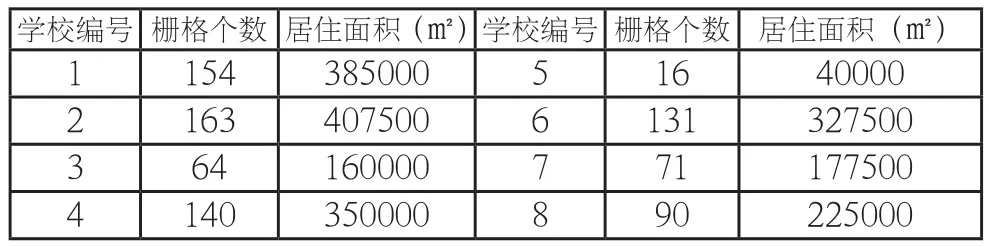
表1 各学校服务区划分结果

6 总结

通过GIS中的网络分析法划分中小学的学区范围既可以避免传统缓冲区法无法无缝衔接的问题，确保所有区域照顾到位，又可以避免泰森多边形法的数据失真问题，提高计算精度，具有较强的理论价值和实践作用，是一种重要的空间技术方法。实际生活中，商场、医院、社区服务中心、消防站、公园等公共设施和中小学一样都需要划分一定的服务范围，确保使用者与服务设施之间的距离能够保持在合理的范围内，因此，网络分析法也可以应用到上述设施的服务范围划分上，具有推广应用的可行性和必要性。