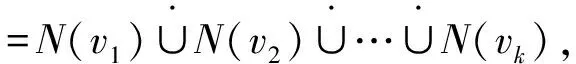几类特殊图的符号差
,
(上海理工大学 理学院,上海 200093)
1 基本概念及背景介绍
本文研究的图都是无环、无重边的简单图.令G=(V,E)是n阶的图,顶点集为V(G)={v1,v2,…,vn},边集为E=E(G).G的邻接矩阵A(G)=(aij),当且仅当vi和vj之间有边连,aij=1;否则,aij=0.邻接矩阵的正特征值个数、负特征值个数、零特征值个数分别称为图的正惯性指数、负惯性指数、零度,分别记为p(G),n(G)和η(G). 正、负惯性指数之差称为图的符号差,记为s(G).正、负惯性指数之和称为图的秩,记为r(G).n阶的完全图、路、圈、星图分别记为Kn,Pn,Cn,K1,n-1.N(v)表示v点的邻点集合,d(v)表示v点的度.若图G满足|E(G)|=|V(G)|+k-1,其中,|E(G)|是图G的边数,|V(G)|是图G的点数,则图G称为k圈图.由k个仅相交于一个点的圈构成的图(图1)称为α-图,连接起点和终点的k条内点不交的路构成的图(图2)称为θ-图.φ1={所有恰含一个α-图作为导出子图的k圈图}和φ2={所有恰含一个θ-图作为导出子图的k圈图}是两类k圈图.对于给定的H∈φ1∪φ2,H所含的导出子图a-图或θ-图称为图H的核,记为χH.对于每一个点v∈χH,将包含顶点v且不包含χH上其他点的H的最大连通导出子图记为H{v},易知H{v}是一棵树.
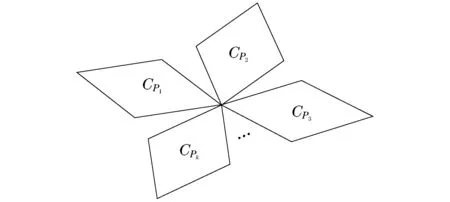
图1 k个仅相交于一个点的圈构成的图Fig.1 Graph made up of k cycles onlyintersected by one point
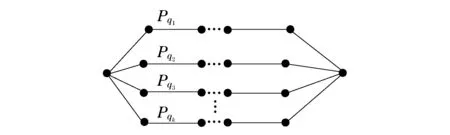
图2 连接起点和终点的k条内点不交的路构成的图Fig.2 Graph made up of k roads that connect thestarting point and the end point and arenon-intersected by the internal points
因为,分子的稳定性和分子图的零度有关,所以,吸引了一大批学者对图的零度进行研究.而图的正、负惯性指数和图的零度密切相关,关于图的正、负惯性指数的研究也引起了学者们的重视.文献[1]提出了一个关于符号差的猜想:
-c3(G)≤s(G)≤c5(G)
(1)
式中,c3(G)和c5(G)分别表示G中长为4k+3和4k+5 (k为非负整数)的圈的数目.
2012年,文献[1]证明了任意简单图的符号差满足s(G)≤c1(G),其中,c1(G)表示G中的奇圈数,并证明了树、单圈图和双圈图对于式(1)成立.2014年,文献[2]证明了简单图的线图对于式(1)成立.2014年,文献[3]证明了边不交圈的图的符号差满足猜想.2015年,文献[4]构造了一些满足式(1)的k圈图.2016年,文献[5]研究了符号差等于奇圈数的图所满足的条件.本文证明了n阶图G中若存在点v,满足d(v) 令A,B是n阶的实对称矩阵,若存在n阶的可逆矩阵P,使得PTAP=B,则称A和B合同,记为A≃B. 引理1[1]若G是树、单圈图或双圈图,则-c3(G)≤s(G)≤c5(G). 引理2[6]令A,B是同阶的实对称矩阵,且A≃B,则p(A)=p(B),n(A)=n(B),η(A)=η(B),s(A)=s(B). 引理4(特征值交错定理)[7]若A是实对称矩阵,B是A的主子矩阵,则B的特征值交错于A的特征值.特别地,若n阶的图G有特征值λ1≥λ2≥…≥λn,且H是G的一个删点子图,有特征值μ1≥μ2≥…≥μn-1,则λi≥μi≥λi+1,1≤i≤n-1. 引理5设v是图G中的一点,则 s(G)-s(G-v)≤1 r(G)-2≤r(G-v)≤r(G) 证明设n阶的图G有特征值λ1≥λ2≥…≥λr≥…≥λs-1≥λs≥λs+1≥…≥λs+r≥λs+r+1≥…≥λn.设H=G-v,H有特征值μ1≥μ2≥…≥μr≥…≥μs-1≥μs≥μs+1≥…≥μs+r≥μs+r+1≥…≥μn-1.由特征值交错定理可知,λ1≥μ1≥λ2≥μ2≥…≥λr≥μr≥…≥λs-1≥μs-1≥λs≥μs≥λs+1≥μs+1≥…≥λs+r≥μs+r≥λs+r+1≥μs+r+1≥…≥μn-1≥λn,设λs为λi(1≤i≤n)里面最后一个正数. a. 若μs>0,则p(G)=p(H);若μs+r=0,则n(G)-1=n(H);若μs+r<0,则n(G)=n(H). b. 若μs<0,则p(G)-1=p(H),n(G)=n(H). c. 若μs=0,则p(G)-1=p(H);若μs+r=0,则n(G)-1=n(H);若μs+r<0,则n(G)=n(H). 则对应的r(G)和s(G)可以表示为: a.r(G)-1=r(H)或r(G)=r(H);s(G)+1=s(H)或s(G)=s(H). b.r(G)-1=r(H);s(G)-1=s(H). c.r(G)-2=r(H)或r(G)-1=r(H);s(G)=s(H)或s(G)-1=s(H). 综上所述,r(G)-2≤r(G-v)≤r(G),|s(G)-s(G-v)|≤1. 引理6[2]设v是图G的一个点,若r(G-v)=r(G)或r(G-v)=r(G)-2,则s(G)=s(G-v). 图G的一个匹配是指G的一个独立边集,图G含边最多的一个匹配称为G的一个最大匹配.设G是一个图,v∈V(G).若存在G的一个最大匹配覆盖点v,则称点v是G的一个可匹配点;否则,称点v是G的一个不可匹配点.若图G仅由一个点组成,约定这个点是G的不可匹配点. 设图G1和图G2顶点不相交,u∈V(G1),在G1∪G2中将点u和G2的任意k个点连接得到的图称为G1和G2的关于点u的一个k-连图,记为G1(u)⊙kG2.注意,当k小于G2的阶数时,图G1(u)⊙kG2并不唯一. 引理7[1]设G是n阶图,u是树T的一个可匹配点,则对每一正整数k(1≤k≤n),有 a.p(T(u)⊙kG)=p(T)+p(G); b.n(T(u)⊙kG)=n(T)+n(G); c.η(T(u)⊙kG)=η(T)+η(G). 引理8-c3(Kn)≤s(Kn)≤c5(Kn)成立. 其中,4k+3是小于n的最大整数,且k为整数.显然, 综上所述,-c3(Kn)≤s(Kn)≤c5(Kn)成立. 引理9设e是Kn中的任意一条边,则-c3(Kn-e)≤s(Kn-e)≤c5(Kn-e)成立. 证明当n≤3时,结论显然成立.以下假设n≥4,设Kn-e的邻接矩阵为A,排列一下Kn-e中点的位置,则邻接矩阵A可写为 经计算,|λE-A|=λ[λ2-(n-3)λ-2(n-2)](λ+1)n-3.故p(Kn-e)=1,n(Kn-e)=n-2,η(Kn-e)=1,从而,s(Kn-e)=p(Kn-e)-n(Kn-e)=3-n<0≤c5(Kn-e).以n3(Kn-e)表示Kn-e中3-圈的个数,则 故-c3(Kn-e)≤2-n,从而s(Kn-e)≥-c3(Kn-e). 综上所述,-c3(Kn-e)≤s(Kn-e)≤c5(Kn-e)成立. 定理1若n阶图G中存在点v,满足d(v) 证明设G是由Kn删k条边得到的n阶图.若k=0或k=1,由引理8和引理9可知结论成立.下面假设k≥2. 由于图G中存在点v满足d(v) 推论1若G中存在孤立点,则-c3(G)≤s(G)≤c5(G). 证明设H=G-v,则 故r(G)=r(G-v),由定理1可知,-c3(G)≤s(G)≤c5(G). 定理2设H是k圈图,若存在点v∈χH是H{v}的可匹配点,则H满足-c3(H)≤s(H)≤c5(H). 证明对于k=0(树),k=1(单圈图),结论成立.下面假设k≥2. 因为,存在点v∈χH是H{v}的可匹配点,且H是H{v}⊙2(H-H{v})中的一个图,则由引理7可知,p(H)=p(H{v})+p(H-H{v}),n(H)=n(H{v})+n(H-H{v}),故p(H)-n(H)=[p(H{v})-n(H{v})]+[p(H-H{v})-n(H-H{v})],即s(H)=s(H{v})+s(H-H{v}).由于v∈χH,则v属于某个圈,删去H{v}至少会破坏一个圈,故H-H{v}的每一个连通分支都满足圈数小于k.假设H-H{v}的所有连通分支为H1,H2,…,Hm,由归纳法可知,-c3(Hi)≤s(Hi)≤c5(Hi)(i=1,…,m),从而有 由引理3可知, 由c3(H),c5(H)的定义可知,-c3(H-H{v})≤s(H-H{v})≤c5(H-H{v}).由于H{v}是树,则s(H{v})=0,从而s(H)=s(H-H{v}).而删点子图中的圈数不会超过原图中的圈数,则-c3(H)≤s(H)≤c5(H). 推论2设G是n(n≥2)阶的图,若G中存在不相邻的两点u,v,满足N(u)=N(v),则-c3(G)≤s(G)≤c5(G). 证明由于uv∉E(G)且N(u)=N(v),所以,A(G)中u,v对应的两行完全相同,故r(G)=r(G-v)成立,由定理1可知,-c3(G)≤s(G)≤c5(G). 证明因为,N(u)是N(v1),N(v2),…,N(vk)的不交并,所以,在G的邻接矩阵中可以通过v1,v2,…,vk对应的行将u对应的行变为全零行.故r(G)=r(G-u)成立,且u和v1,v2,…,vk不相连,因此,d(u) 推论4设G是n(n≥3)阶的图,若G中存在悬挂点,则-c3(G)≤s(G)≤c5(G). 证明G的邻接矩阵可写为 其中,1对应的是悬挂点v,则r(G)=r(G-v)+2,且d(v) [1] MA H C,YANG W H,LI S G.Positive and negative inertia index of a graph[J].Linear Algebra and its Applications,2013,438:331-341. [2] WANG L,FAN Y Z.The signature of line graphs and power trees[J].Linear Algebra and its Applications,2014,448:264-273. [3] JIANG Y M.The signature of edge-disjoint cyclic graphs[J].Advances in Mathematics (China),2014,43(6):863-868. [4] WANG D Y,TIAN F L.The signature ofk-cyclic graphs of ∞-type[J].Linear and Multilinear Algebra,2016,64(3):375-382. [5] MA X B,WONG D,TIAN F L.Characterization of graphs whose signature equals the number of odd cycles[J].Linear Algebra and its Applications,2016,511:259-273. [6] LANCASTER P,TISMENETSKY M.The theory of matrices[M].2nd ed.Orlando,FL:Academic Press,1985.2 主要引理
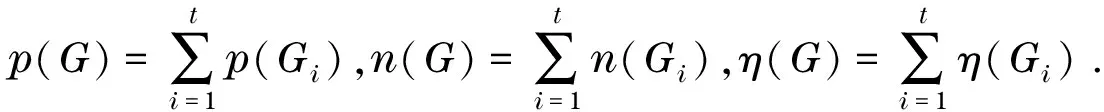
3 主要结论
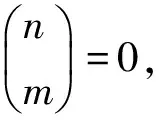

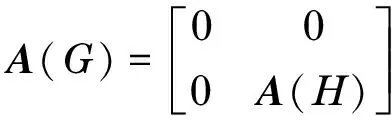
4 满足r(G)≠r(G-v)+1的特殊图