基于缝翼位置参数的多段翼型噪声性能分析
王红建,罗望,张锐
(西北工业大学 航空学院,西安 710072)
0 引 言
随着科学技术的高速发展,现代民航工业已将飞机的绿色环保、安静舒适纳入研究范畴。同时,由于高涵道比发动机的出现以及发动机降噪技术的不断成熟,发动机噪声得到了显著降低,致使机体噪声成为了飞机总噪声的重要来源[1]。众多实验研究表明,缝翼噪声是大型客机起降过程中机体噪声的主要贡献者之一[2-8]。因此,研究前缘缝翼的发声机理、探索有效的缝翼降噪技术,对新一代民航飞机噪声性能的提高具有重要意义。
缝翼因其特殊的几何外形,使得流体流经其外表面时形成复杂的流动形态,尤其是在缝翼前缘尖点(cusp)处生成的剪切层的发展变化以及缝翼凹面回流区内的流动演化,均十分复杂。因此,缝翼近场流动及其噪声源的生成机理一直都是缝翼噪声研究的热点[8]。
研究表明,缝翼噪声主要包括三个典型部分:宽频噪声[3,8]、高频窄带噪声[2,9]、在低频部分的多峰值窄带噪声[3,7,10]。高频窄带噪声是由于缝翼尾缘涡脱落产生的[11],这一现象通常只在等比例缩小模型上才会出现。对于宽频噪声,尽管其机理目前尚未明确,但有研究表明宽频噪声与缝翼空腔内剪切层和缝翼压力面的相互作用有关[8,12-13]。目前,对于低频多峰值噪声产生的机理同样未有明确定论,但随着谐振和声反馈相关模型的提出[7,14-15],越来越多的证据表明Rossiter-type原理[16]是这种低频多峰值噪声产生的原因[15]。
改变缝翼位置参数会改变缝翼/翼型的流动状态,并对缝翼噪声产生重要影响,因此,缝翼位置参数始终是研究的热点。S.Olson等[17]研究发现,缝翼位置参数能够影响缝翼压力场,并主导着涡脱落以及产生噪声的共振反馈机制。随着缝翼与主翼之间缝道宽度或缝翼角度的增加,宽频噪声随之增加[4,18-20],但获得上述结论的试验[4,18,20]和数值模拟[19]所涉及的参数比较有限,且主要关注的是缝翼噪声的宽频部分。另有研究发现,缝翼角度增加会产生多与涡脱落机理有关的气动噪声。例如,M.R.Khorrami等[11]在进行三维数值仿真时发现,当缝翼角度从30°减小至20°的过程中,由于缝翼钝后缘引起的涡脱落导致的高频峰值噪声被强烈抑制了。改变缝翼与主翼之间的缝道宽度不会对由缝翼尾缘发声的频率产生显著影响[21-22]。C.C.Pagani等[23]通过实验分析了不同缝翼角度、重叠量、缝道宽度对缝翼噪声的影响特性,发现产生最小噪声所对应的缝翼位置与考虑气动力优化的基准位置完全不同。刘志仁等[24]通过仿真发现,当缝道宽度减小而重叠量增加时,噪声总声压级持续减小,缝道宽度与重叠量都很大或很小时,噪声总声压级显著增大;但该研究只考虑了缝道宽度与重叠长度的影响,并未考虑缝翼角度的影响。
本文在上述研究的基础上,综合考虑缝翼角度、缝道宽度和重叠长度的改变,利用数值仿真方法,研究缝翼不同位置对其流场特性及噪声特性的影响规律;着重研究缝翼位置改变对翼型气动力及缝翼远场噪声的作用规律。
1 缝翼噪声分析模型
选用麦道公司(现已并入波音公司)的30P-30N二维机翼作为研究对象,该翼型包括缝翼、主翼和襟翼三部分。当缝翼和襟翼收起来时,称为干净翼型,为了便于和NASA PIV[25]实验进行对比,选取干净翼型的模型弦长c为0.457 m。在原始位置下,缝翼、襟翼与主翼的偏角均为30°。缝翼缝道宽度(Gap,简称G)为2.95%c,缝翼交叠量(Overhang,简称OP)为-2.5%c;襟翼缝道宽度为1.7%c,襟翼交叠量为0.25%c。30P-30N机翼外形及其细节如图1~图2所示[26]。
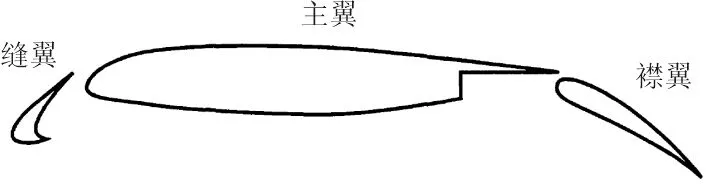
图1 30P-30N外形Fig.1 Shape of 30P-30N
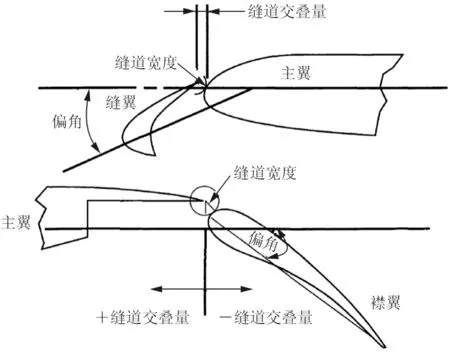
图2 30P-30N细节Fig.2 Details of 30P-30N
2 缝翼流场分析
2.1 流场网格划分
采用C型结构网格计算,网格节点约为3×105,计算区域约为25倍机翼巡航弦长。为了保证缝翼空腔内非定常流动的精准性,在缝翼空腔内采用网格加密处理。边界层划分25个节点,为了保证计算的收敛性,第一层附面层网格满足y+= 0.3~1.2,其具体网格如图3~图4所示。

图3 30P-30N结构网格Fig.3 Structured mesh of 30P-30N model

图4 缝翼处网格Fig.4 Grids in the vicinity of slat
2.2 流场仿真分析
首先,基于SSTk-ω湍流模型初始化流场,压力速度耦合方法选用SIMPLE算法,由于网格横纵比较大,空间离散方法采用双精度格式计算,若监测到的升力系数与阻力系数的变化小于0.1%,则认为流场稳定,将上述计算结果作为非定常计算的初始值;其次,将上一步计算得到的初始值采用基于LES大涡模拟模型进行非定常计算,计算时间步长为6 000步,以消除稳态流场的影响;最后,继续采用LES大涡模拟模型计算瞬态流场,同时引入FW-H声学模型求解噪声,FW-H积分面选择缝翼外壁面作为声源面来求解远场噪声,计算步长为15 000步,得到的数据用以统计分析远场噪声特性,其无量纲时间步长为2×10-6。计算条件为:攻角α=8°,来流速度M∞=0.17Ma,Re=1.7×106。
2.3 计算方法验证
为了验证仿真的正确性,采用来流速度为0.2Ma,攻角α=8°,将流场分析所得表面压力系数时均值与NASA实验结果[26]进行对比,如图5所示,可以看出:本文计算结果与实验结果吻合较好。
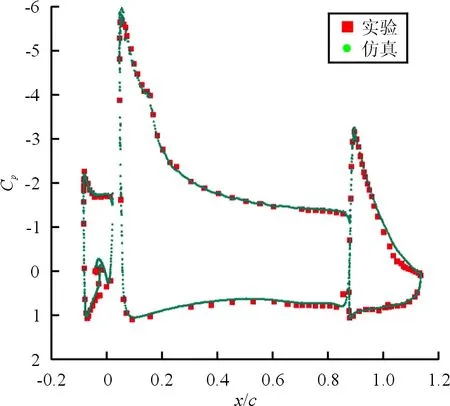
图5 压力分布仿真结果与实验对比Fig.5 Comparison of surface pressure distribu- tion between simulation and experiment
α=8°,M∞=0.17Ma条件下,时间平均后,仿真与PIV实验[25]沿流线方向速度云图U/U∞、沿流线垂线方向速度云图V/U∞分别如图6~图7所示,可以看出:仿真结果与实验结果基本吻合。
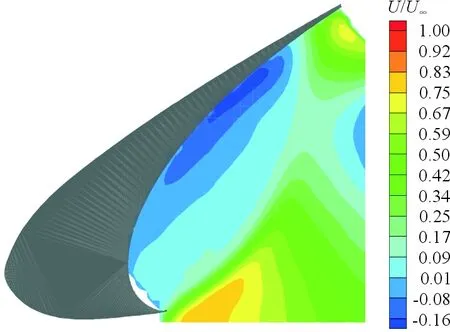
(a) PIV实验
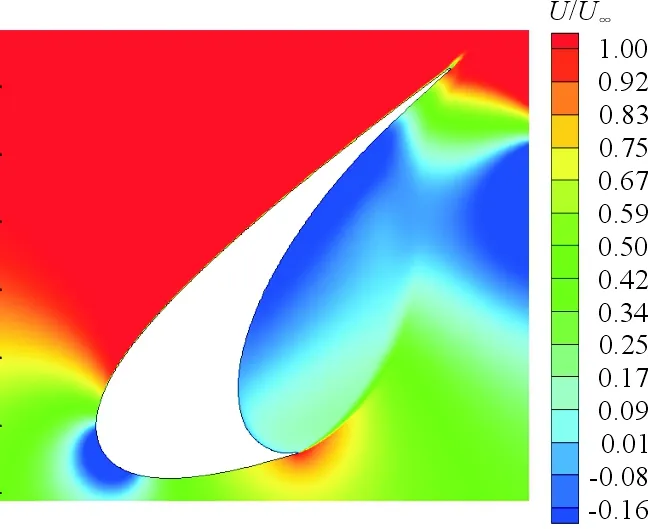
(b) 仿真图6 U/U∞对比图Fig.6 Comparison of U/U∞ between simulation and experiment
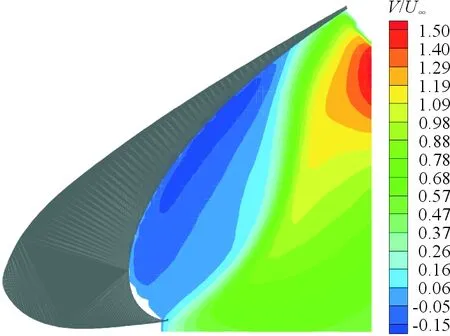
(a) PIV实验
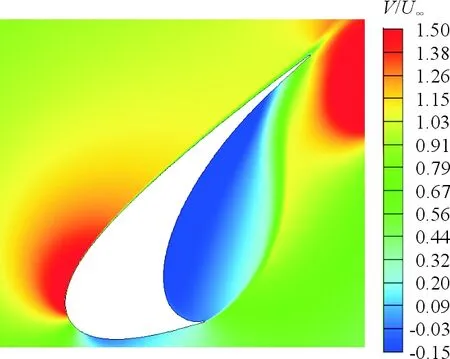
(b) 仿真图7 V/U∞对比图Fig.7 Comparison of V/U∞ between simulation and experiment
α=8°,PIV实验缝翼空腔位置的流线图与数值仿真时间平均后的流线图的对比,如图8所示,可以看出:仿真得到的流线图与PIV实验吻合较好,平均回流在附着点位置为11.16 mm,与PIV实验的10.93 mm十分接近。
2.4 剪切层压力脉动
为了研究噪声源的频率特性,在缝翼空腔内沿剪切层的起点、中点和终点附近,分别布置三个压力脉动监测点,用来监测近场噪声,如图9所示。
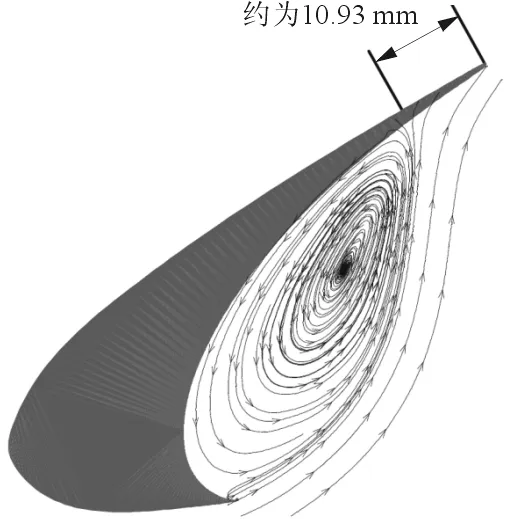
(a) PIV实验
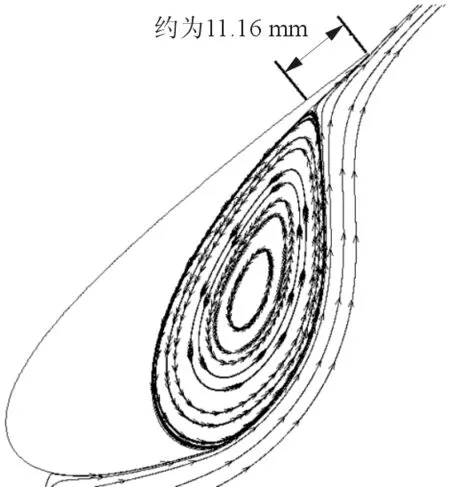
(b) 仿真图8 空腔处流线对比Fig.8 Comparison of streamline at the cavity between simulation and PIV experiment
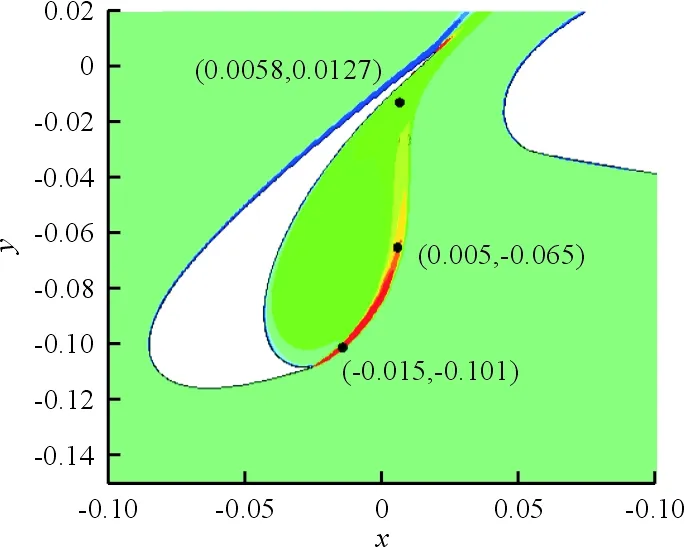
图9 压力脉动监测点Fig.9 Microphone positions of pressure pulsation
不同监测点的噪声频谱如图10所示,可以看出:点1处的噪声最小,点3处的噪声最大,反映了缝翼尾缘附近由于剪切层涡流与缝翼尾缘壁面碰撞产生高分贝噪声的特性;缝翼噪声具有明显的宽频特性,主要能量集中在低频到中频段,且随着频率的增加而衰减。
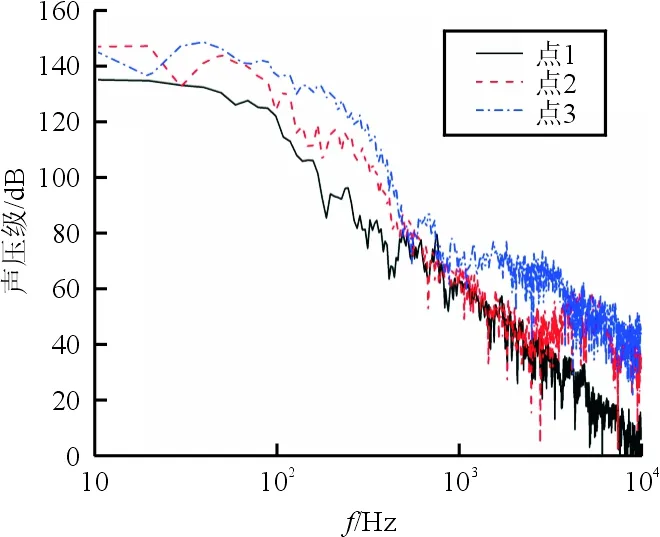
图10 不同监测点噪声频谱Fig.10 The noise spectrum in different microphone positions
3 缝翼位置参数的影响
3.1 远场噪声计算
为了研究前缘缝翼远场噪声的特性,对缝翼原始位置进行分析,在非定常流场中引入FW-H声学模型来计算噪声,FW-H积分面选择缝翼外固壁面,进行15 000次迭代后得到了噪声声压数据。在距离模型50倍巡航弦长处的圆周上每隔5°布置一个远场噪声观测点,得到缝翼噪声指向性图,如图11所示,可以看出:缝翼噪声辐射为一偶极子形态,与缝翼产生噪声的机理一致。
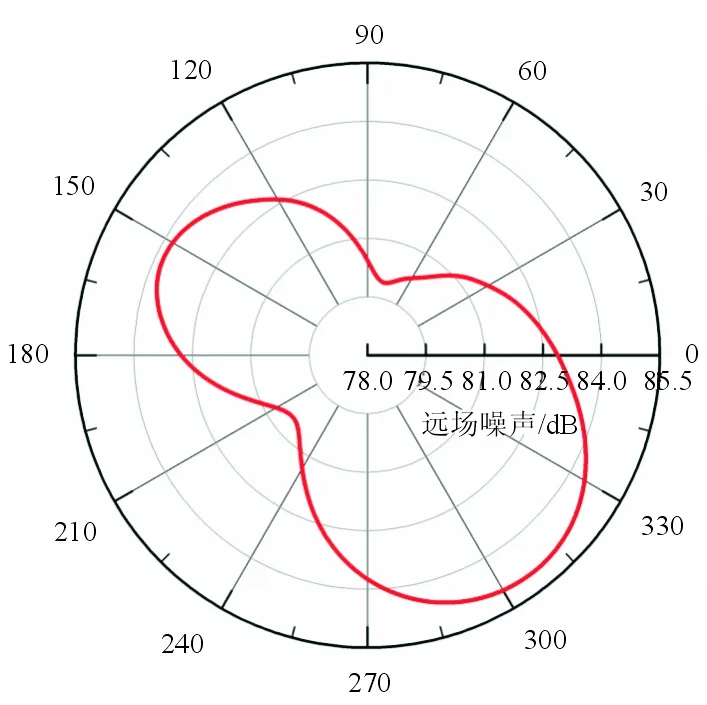
图11 原始位置下缝翼远场噪声指向性图Fig.11 The Far field directivity pattern of slat noise in original position
3.2 缝翼位置参数对噪声的影响
为了研究缝翼位置改变对缝翼远场噪声(即流场特性)的影响,从以下两种情况进行分析:①重叠长度、缝道宽度均保持在原始位置不变,只改变缝翼偏转角αslat;②令缝翼偏转角αslat不变,研究重叠长度、缝道宽度同时作用下的远场噪声及气动力特性。
3.2.1 缝翼偏转角度αslat的影响
以30P-30N的基准模型作为参考,在保证缝翼缝道宽度为2.95%c且重叠长度为-2.5%c不变的基础上,研究前缘缝翼在10°~38°偏转范围内的气动及噪声特性。角度偏转值分别为10°、16°、20°、22°、24°、26°、27°、28°、29°、30°、31°、32°、34°和38°。按照上一步计算远场噪声的方法,在距离模型50倍机翼巡航弦长下,每隔22.5°设置一个观测点,共计16个观测点,计算该16个观测点噪声声压平均值(OASPL Average,简称OASPLA),计算结果如图12所示。前缘缝翼在不同偏角下,稳态流场下的气动特性(用气动升力系数的变化来反映)如图13所示。
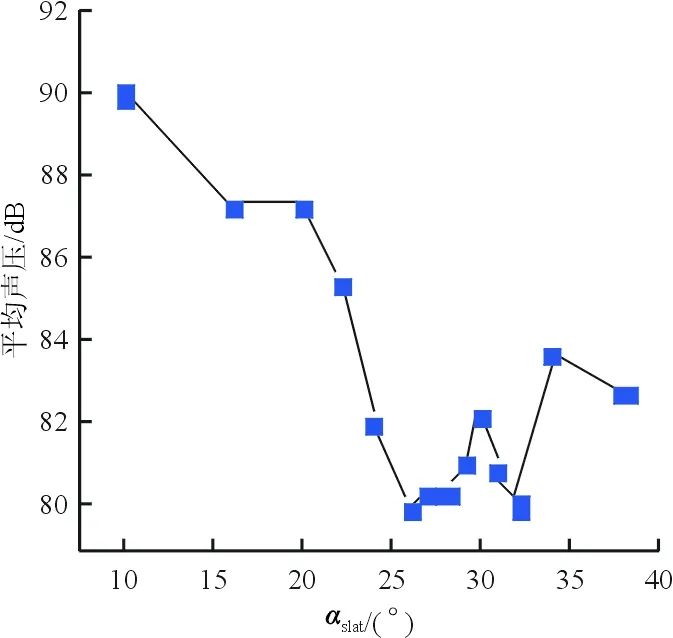
图12 不同角度下的缝翼平均声压Fig.12 The OASPLA at different angles
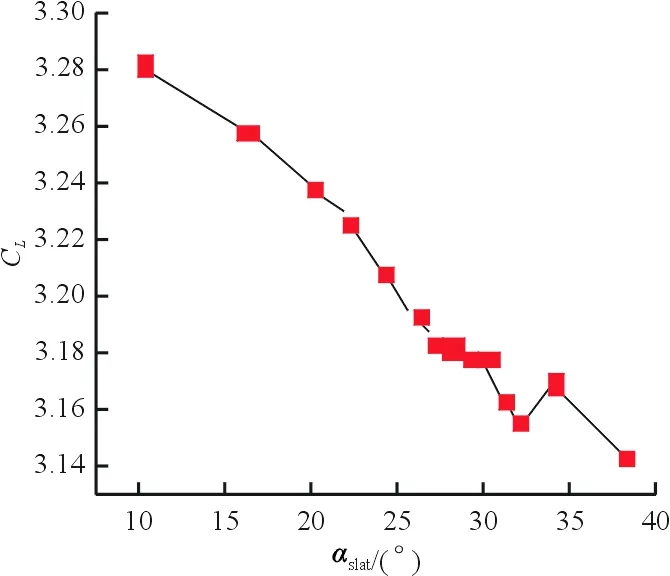
图13 不同角度下的多段翼升力系数Fig.13 The airfoil lift coefficient at different angles
从图12~图13可以看出:在气动升力系数没有减小的条件下,当αslat=26°时,可有效降低远场噪声的总声压级。
缝翼角度在26°、30°和34°三个典型位置的时均涡量图及湍动能云图分别如图14~图15所示,可以看出:当αslat=26°时,缝翼空腔内的涡量强度、湍动能强度均处于最小;在缝翼空腔与靠近剪切层附近,湍流强度的大小基本反映了远场噪声的声压级大小,证明剪切层湍流与缝翼后缘壁面的相互影响的剧烈程度对缝翼远场噪声具有重要影响。
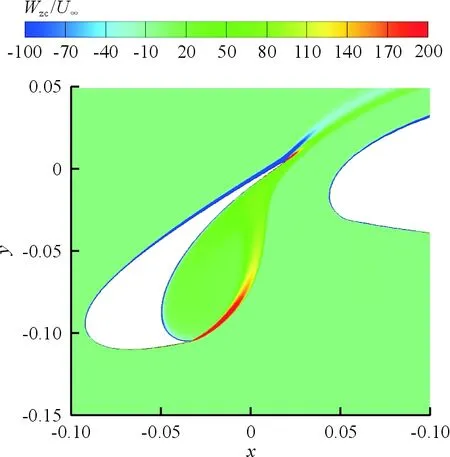
(a) αslat=26°
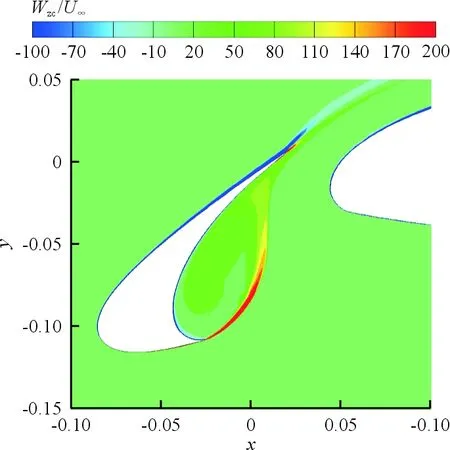
(b) αslat=30°
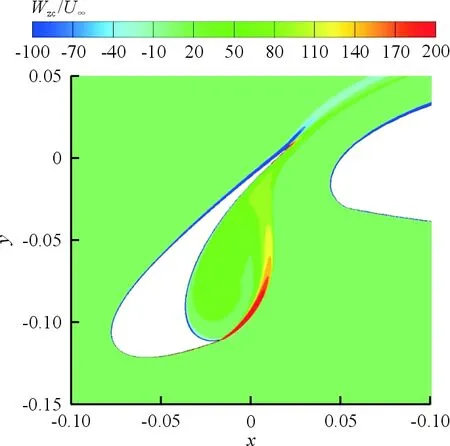
(c) αslat=34°图14 典型状态下的时均涡量Fig.14 Average vorticity under typical conditions
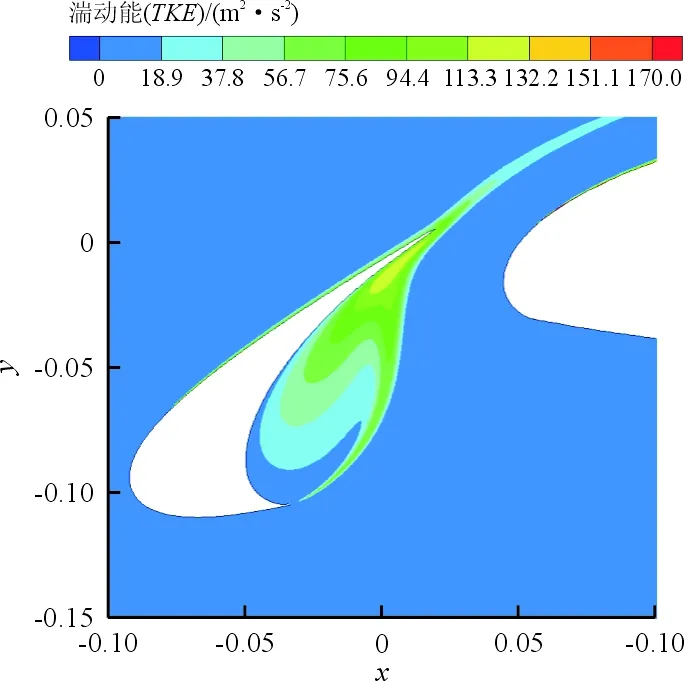
(a) αslat=26°
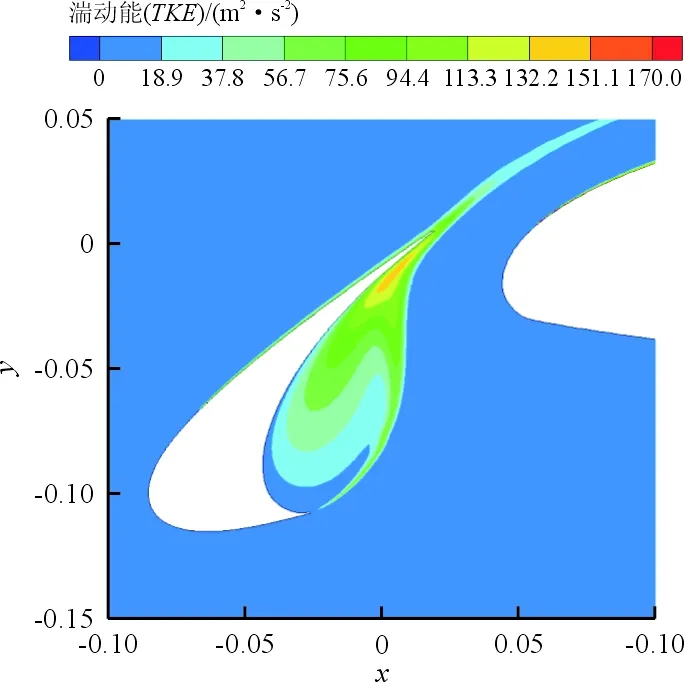
(b) αslat=30°
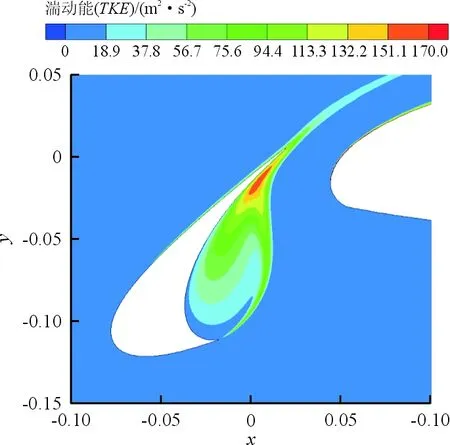
(c) αslat=34°图15 典型状态下湍动能Fig.15 Turbulent kinetic energy under typical conditions
3.2.2 缝道宽度及重叠长度的影响
当缝道宽度减小而重叠量增加时,噪声总声压级持续减小;缝道宽度与重叠量都很大或很小时,噪声总声压级显著增大[25]。本文根据上述结论,选择αslat=26°并保持不变时,改变缝道宽度和重叠长度,计算其缝翼噪声平均声压级OASPLA。位置选择情况和计算结果如表1所示。

表1 不同缝翼位置下的噪声Table 1 Slat noise in different slat configuration parameters
为了进一步分析不同缝翼位置下的远场噪声特性,计算表1中五个不同缝翼位置参数下50倍弦长的远场噪声,其相性图如图16所示(坐标轴表示远场噪声,单位是dB),可以看出:各缝翼远场噪声指向性图均接近于偶极子,且当缝翼位置处于缝道宽度1.0%c、重叠长度-0.5%c时,噪声最小。
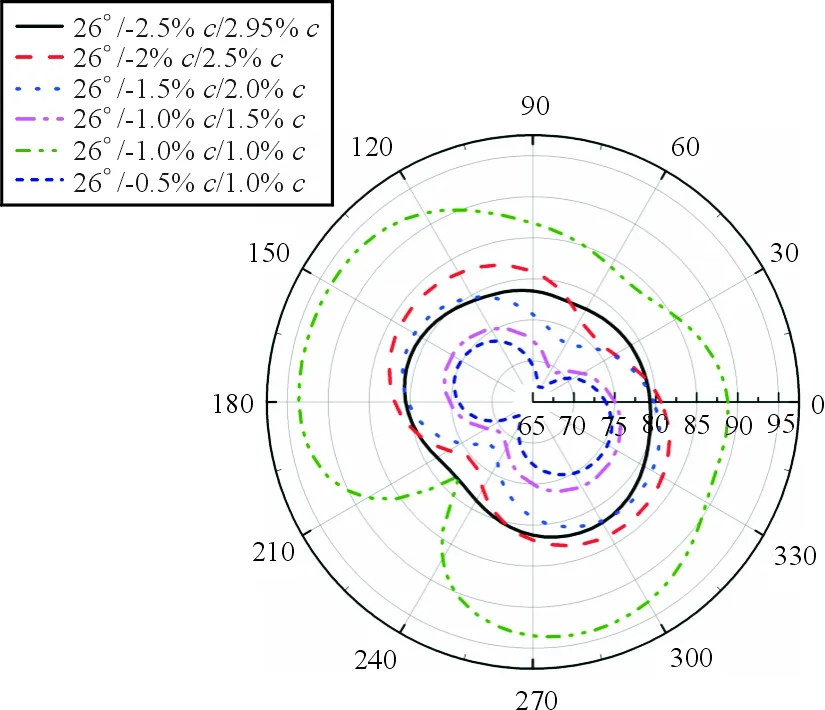
图16 不同位置下的远场噪声指向性图Fig.16 Far field directivity pattern of slat noise in different slat configuration parameters
通过对比发现,在距离机翼50倍弦长且角度在310°下,远场噪声最大。因此,在310°下距离机翼50c处设置一个远场噪声监测点,不同位置下该点的远场噪声频谱图如图17所示;并着重对比频率范围在100~10 000 Hz下的远场噪声频谱,如图18所示。
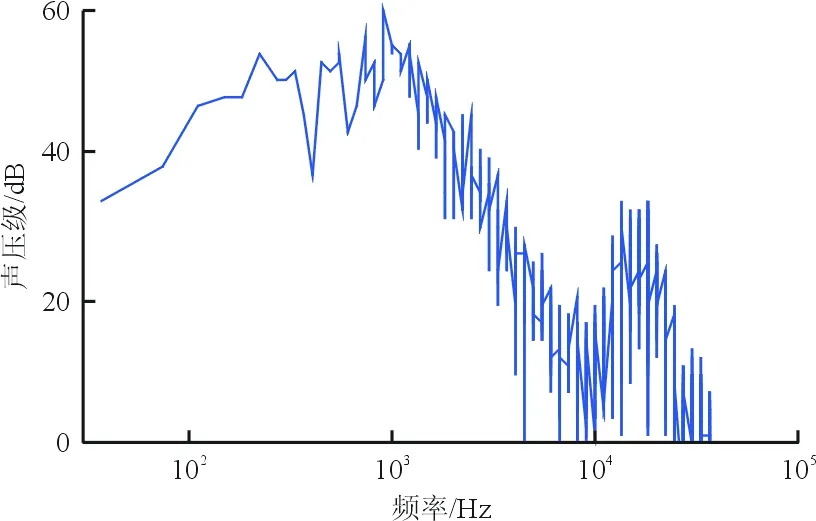
(a) 缝道宽度2.5%c,重叠长度-2.0%c
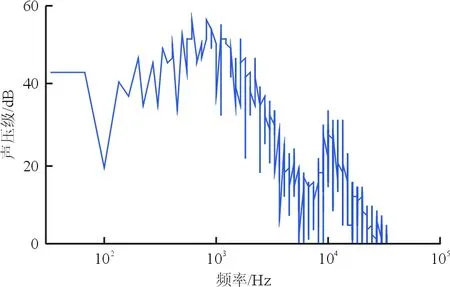
(b) 缝道宽度2.0%c,重叠长度-1.5%c
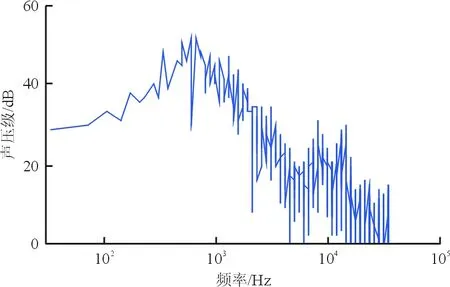
(c) 缝道宽度1.5%c,重叠长度-1.0%c
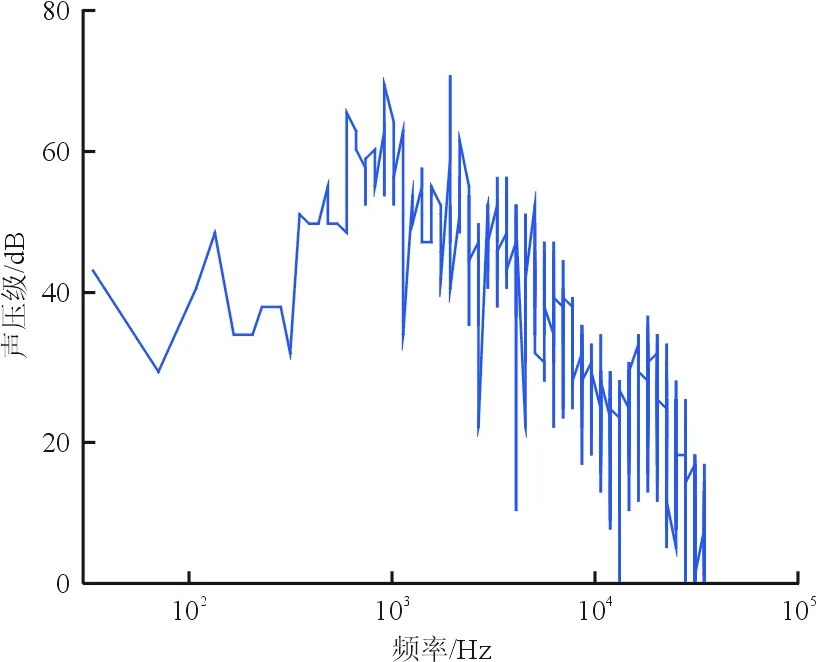
(d) 缝道宽度1.0%c,重叠长度-1.0%c
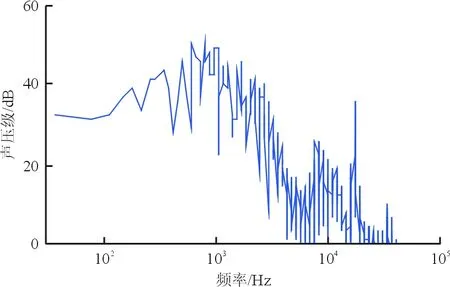
(e) 缝道宽度1.0%c,重叠长度-0.5%c图17 不同缝翼位置下的频谱图Fig.17 Noise spectrum in different slat configuration parameters
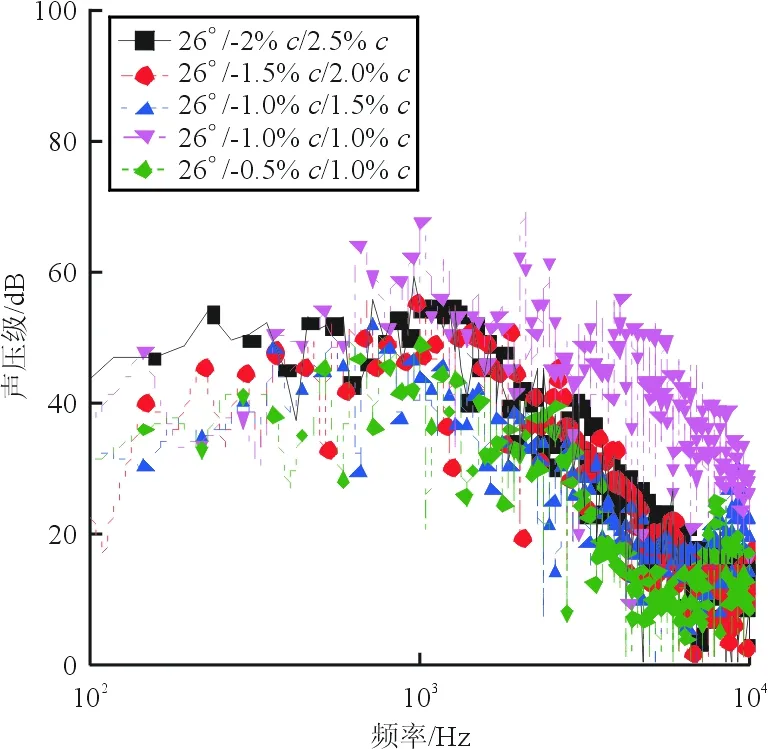
图18 不同位置下远场声压级频谱Fig.18 The slat noise in different slat configuration parameters
从图17~图18可以看出:当缝道宽度减小而重叠长度增大时,缝翼噪声减小,且噪声减小段主要在中低频范围内;对比重叠长度均为-1.0%c,缝道宽度分别为1.5%c和1.0%c的状态,发现当缝道宽度变为1.0%c时远场噪声明显增大,这可能是由于缝翼在此位置相对于主翼位置太过偏下,对流场状态改变有较大影响。
4 结 论
(1) 当缝翼角度在10°~26°范围内,缝翼噪声随缝翼角度的增大而减小;当缝翼角度在26°~30°范围内,缝翼噪声随缝翼角度的增加而增加;当缝翼处于26°且在50倍弦长下,远场噪声减小了约2 dB。
(2) 当缝翼角度进行小角度改变,例如26°~34°,升力系数的变化不大,即对升力特性的影响不大。
(3) 通过调整缝翼角度、缝道宽度以及重叠长度,能够在保证升力系数不受折损的前提下,有效降低缝翼噪声;当缝翼处于26°/-0.5%c/1.0%c参数下,在50倍弦长下远场噪声降低约8 dB。
(4) 优化缝翼位置参数是提高翼型气动性能、控制缝翼噪声的一种有效途径。
[1] Dobrzynski W. Almost 40 years of airframe noise research: what did we achieve?[J]. Journal of aircraft, 2010, 47(2): 353-367.
[2] Storms B L, Hayes J A, Moriarty P J, et al. Aeroacoustic measurements of slat noise on a three-dimensional high-lift system[R]. AIAA-99-1957, 1999.
[3] Dobrzynski W, Nagakura K, Gehlhar B, et al. A airframe noise studies on wings with deployed high-lift devices[R]. AIAA-98-2337, 1998.
[4] Mendoza J F, Brooks T F, Humphreys W M. Aeroacoustic measurements of a wing/slat model[R]. AIAA-2002-2604, 2002.
[5] Smith M, Chow L. Aerodynamic noise sources on high lift slats and flaps[R]. AIAA-2003-3226, 2003.
[6] Imamura T, Ura H, Yokokawa Y, et al. A far-field noise and near-field unsteadiness of a simplified high-lift-configuration model(slat)[R]. AIAA-2009-1239, 2009.
[7] Kolb A, Faulhaber P, Drobietz R, et al. Aeroacoustic wind tunnel measurements on a 2d high-lift configuration[R]. AIAA-2007-3447, 2007.
[8] Dobrzynski W, Pott-Pollenske M. Slat noise source studies for farfield noise prediction[C]∥7th AIAA/CEAS Aeroacoustics Conference and Exhibit, 2001: 2158.
[9] Choudhari M M, Lockard D P, Macaraeg M G, et al. Aeroacoustic experiments in the NASA langley low-turbulence pressure tunnel[R]. NASA/TM-2002-211432, 2002.
[10] Pascioni K, Cattafesta L N, Choudhari M M. An experimental investigation of the 30P30N multi-element high-lift airfoil[C]∥20th AIAA/CEAS Aeroacoustics Conference, 2013:1-13.
[11] Khorrami M R, Berkman M E, Choudhari M. Unsteady flow computations of a slat with a blunt trailing edge[R]. AIAA-99-1805, 1999.
[12] Choudhari M M, Khorrami M R. Effect of three-dimensional shear-layer structures on slat cove unsteadiness[J]. AIAA Journal, 2007, 45(45): 2174-2186.
[13] Molin N, Roger M. The use of Amiet’s methods in predicting the noise from 2D high-lift devices[C]∥6th AIAA/CEAS Aeroacoustics Conference and Exhibit, 2000:2064.
[14] Roger M, Perennes S. Low-frequency noise sources in two dimensional high-lift devices[R]. AIAA-2000-1972, 2000.
[15] Terracol M, Manoha E, Lemoine B. Investigation of the unsteady flow and noise sources generation in a slat cove: hybrid zonal RANS/LES simulation and dedicated experiment[C]∥20th AIAA Computational Fluid Dynamics Conference, 2011: 3203.
[16] Rossiter J E. Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds[R]. London, UK: Aeronautical Research Council, 1966: 3438.
[17] Olson S, Thomas F, Nelson R. A preliminary investigation into slat noise production mechanisms in a high-lift configuration[R]. AIAA-2000-4058, 2000.
[18] Pott-Pollenske M, Alvarez-Gonzales J, Dobrzynski W. Ef-fect of slat gap on farfield radiated noise and correlation with local flow characteristics[C]∥9th AIAA/CEAS Aeroacoustics Conference and Exhibit, 2003: 3228.
[19] Emunds R, Fischer M. Effect of slat settings(gap overlap) on slat noise based on a test vortex injected upstream of the SLAT-Hook[C]∥12th AIAA/CEAS Aeroacoustics Conference, 2006: 2665.
[20] Guo Y P, Yamamoto K J, Stoker R W. Component-based empirical model for high-lift system noise prediction[J]. Journal of Aircraft, 2003, 40(5): 914-922.
[21] Takeda K, Zhang X, Nelson P. Unsteady aerodynamics and aeroacoustics of a high-lift device configuration[R]. AIAA-2002-0570, 2002.
[22] Takeda K, Zhang X, Nelson P A. Computational aero-acoustic simulations of leading-edge slat flow[J]. Journal of Sound & Vibration, 2004, 270(3): 559-572.
[23] Pagani C C, Souza D S, Medeiros M A F. Experimental investigation on the effect of slat geometrical configurations on aerodynamic noise[J]. Journal of Sound & Vibration, 2017, 394: 256-279.
[24] 刘志仁, 王福新, 宋文滨, 等. 二维增升装置前缘缝翼的远场噪声分析[J]. 空气动力学学报, 2012, 30(3): 388-393.
Liu Zhiren, Wang Fuxin, Song Wenbin, et al. Far-field aeroacoustic analysis for slat of a two-dimensional high-lift configuration[J]. Acta Aerodynamica Sinica, 2012, 30(3): 388-393.(in Chinese)
[25] Jenkins L N, Khorrami M R, Choudhari M. Characterization of unsteady flow structures near leading-edge slat: Part I. PIV measurements[R]. AIAA-2004-2801, 2004.
[26] Klausmeyer S, Lin J. Comparative results from a CFD ch-allenge over a 2D three-element high-lift airfoil[R]. NA-SA/TM-1997-112858, 1997.

