台阶式溢洪道相对比能影响因素研究
谭相文
(菏泽市水利局,山东 菏泽 274000)
台阶式溢洪道的历史可以追溯到两千多年以前,最初使用在跌水和塘坝上。随后人们对台阶式溢洪道的消能与泄水功能越来越认可,将其应用到中小型水利工程之中[1]。近年来,中国加大了对台阶式溢洪道的研究和应用,在各地方水电站泄洪中起到了巨大作用,如:江垭水电站、大朝山水电站等。为了解台阶式溢洪道的水力特性,水利工作者对其理论进行了深入的研究与验证。现阶段台阶溢洪道的研究方法包括:理论分析、模型试验、数值模拟、原型观测等[2]。利用能量特性研究台阶结构的水力特性早在19世纪就已经被提出,比能成为非常重要的水力指标[3-4]。本文通过将水力计算理论已成熟的光滑溢洪道,与台阶式溢洪道对应断面的比能进行比较,引入相对比能概念,分析台阶溢洪道相对比能计算理论的必要性,并指出台阶溢洪道相对比能的影响因素,为进一步深入研究台阶溢洪道水利特性提供理论依据[5]。
1 台阶式溢洪道相对比能及计算方法
比能是指以断面最低点为基准,单位重量液体具有的势能与动能之和,其在断面总机械能中可反映水流状况[6]。通过引入相对比能概念,对台阶式溢洪道水流与光滑溢洪道水流从能量角度分析,比较相同条件下光滑溢洪道与台阶溢洪道对应断面比能差值。
ΔES=Esg-Est
(1)
式中Esg——光滑溢洪道断面比能,m;Est——台阶溢洪道对应位置断面比能,m。
光滑溢洪道与台阶溢洪道差值与相对断面比能相同,可知相对比能大则可采用台阶溢洪道,减少水头损失。设台阶溢洪道水深为ht,断面平均流速为vt,则台阶水流比能计算式为
(2)
如将台阶溢洪道的台阶去掉变成光滑溢洪道,在坡度、单宽流量等因素不变的条件下,可得出光滑水流比能计算式为
(3)
式中vi——各断面的平均流速,m/s;hi——各断面的平均水深,m。
2 模型试验概况
通过观测四种不同坡度(48.0°、38.7°、32.0°、26.6°)的台阶溢洪道模型,总结在不同单宽流量台阶高度、坡度及流程长度条件下,断面比能与相对比能变化关系。工程模型具体资料见下表。试验按重力相似准则进行,水深测量以台阶阶顶连线为准,采用测针多次测量取平均值。过流流量用矩形薄壁堰和三角堰测量。
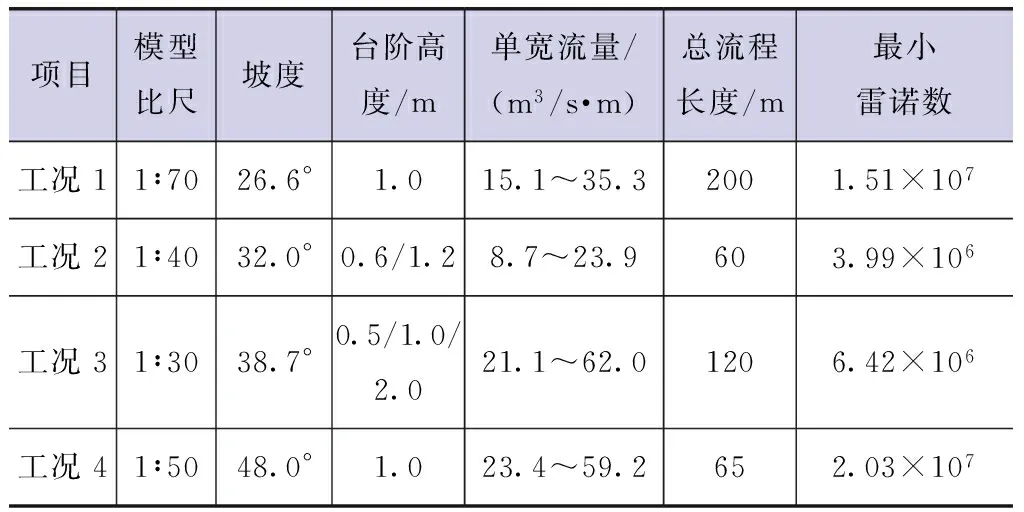
工程试验模型基本资料表
以工况3为分析对象,相对比能、台阶溢洪道比能、光滑溢洪道比能之间的关系见图1。
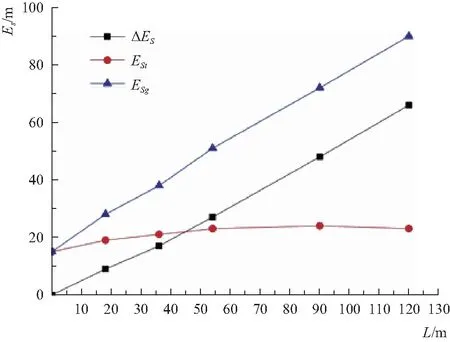
图1 相对比能、台阶溢洪道比能、光滑溢洪道比能沿程变化对比
图1中Es表示水流能量,ΔEs表示同体积光滑溢洪道与台阶溢洪道同断面处比能差值,Est表示台阶水流比能,Esg表示光滑水流比能。分析可知,台阶溢洪道与光滑溢洪道水流断面比能沿程呈现曲线变化,而相对比能呈现良好的线性变化;光滑溢洪道断面比能与相对比能随沿程增加而增大,台阶溢洪道断面比能随沿程增加,先增大后保持平稳。主要原因是光滑溢洪道水深随沿程递减,断面比能随沿程递增,位能主要转化为水流动能;台阶溢洪道通过台阶的旋滚消能,断面比能基本保持不变,位能被台阶损耗,每级台阶水流达到平稳状态。
3 相对比能影响因素分析
3.1 单宽流量
选取工况3模型为研究对象,分析单宽流量与台阶溢洪道相对比能间的关系,试验单宽流量分别为62.2m3/(s·m)、46.6m3/(s·m)、35.7m3/(s·m),水流均为滑行流。不同单宽流量对台阶水流比能与沿程、台阶水流动能与沿程关系的影响如图2、图3所示。
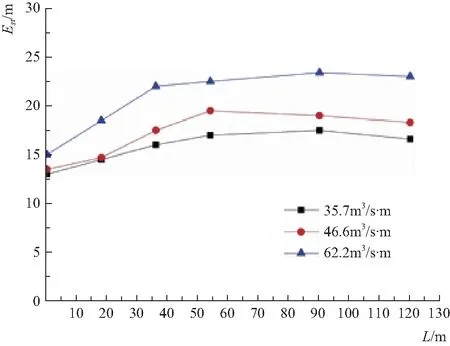
图2 不同单宽条件下断面比能与沿程关系比较
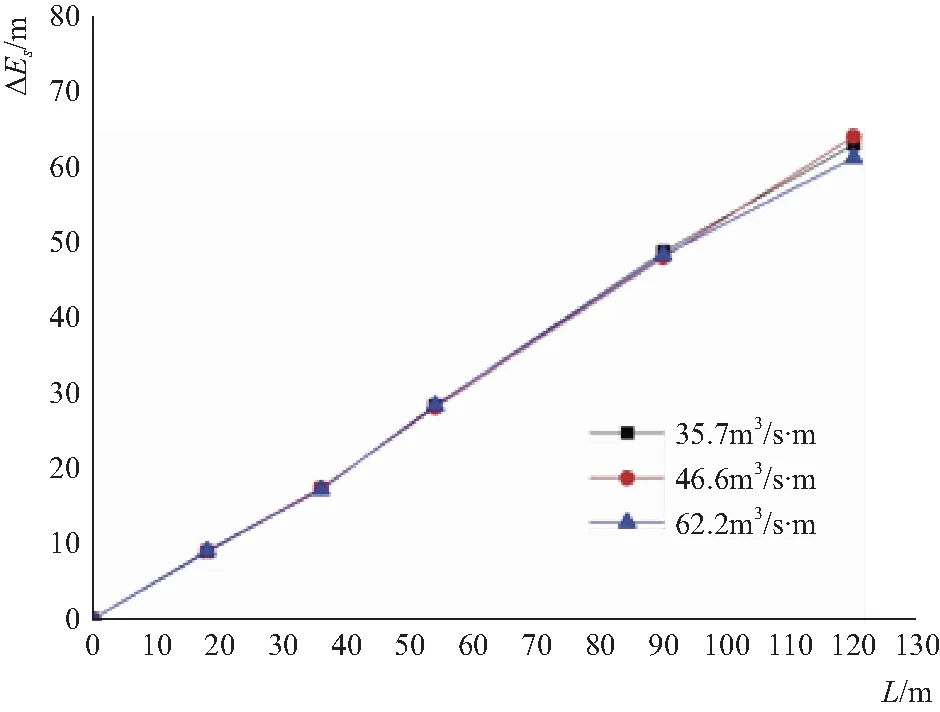
图3 不同单宽条件下相对比能与沿程关系比较
从图2和图3中可以看出,在三种不同单宽流量条件下台阶溢洪道断面比能Est均随流程增加呈现出先增加后平稳的趋势,而相对比能ΔEs则均表现为线性递增趋势,其相关系数为0.9981~0.9997。比较Est与ΔEs规律可以发现,同一断面不同单宽流量时断面比能Est数值不同,共绘制出3条曲线,而相对比能ΔEs数值基本相同,相对误差低于4.5%,可用一条曲线进行模拟说明规律。按照台阶相对比能的物理意义,可得出在同体型条件下台阶溢洪道超出光滑溢洪道的水头损失部分随流程增加而呈线性递增,单位宽度、流程上超出的水头损失是定值,且与单宽流量大小无关。
3.2 台阶高度
选取工况3为研究对象,分析台阶高度与台阶溢洪道相对比能间的关系,试验台阶高度分别为0.5m、1.0m、2.0m,单宽流量为35.7m3/(s·m),水流均为滑行流。坡度相同但台阶高度不同的溢洪道沿程断面比能及相对比能的规律如图4、图5所示。

图4 不同台阶高度条件下断面比能与沿程关系比较
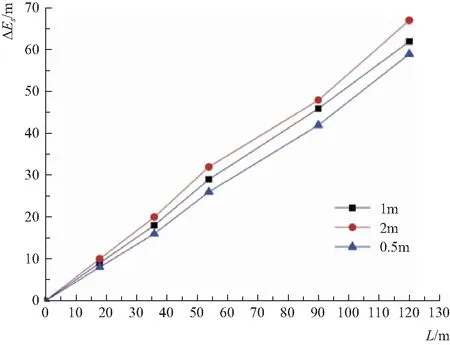
图5 不同台阶高度条件下相对比能与沿程关系比较
从图4中可以看出,在同一流量下不同台阶高度断面比能均呈现随流程增加先升高后稳定的规律,但台阶高度与断面比能之间未表现出良好规律;台阶下游断面比能相对稳定,台阶高度与断面比能间呈负相关关系。在同一流量下不同台阶高度相对比能与流程长度均表现为极显著的线性关系,相关系数在0.9991~0.9995,斜率随高度增加而增加,按台阶高度排列分别为0.510、0.533、0.569,表明台阶越高对水流能量损耗越大,但由于三者间差距不大,说明台阶高度对水头损失的影响有限。综上所述,台阶高度能够影响水流能量的耗损程度,而增加台阶高度对消能有利。
3.3 坡度
选取工况3为研究对象,分析坡度与台阶溢洪道相对比能间的关系,试验台阶坡度分别为1∶0.9、1∶1.25、1∶2,坡角分别为48.0°、38.7°、26.6°,台阶高度为1m,单宽流量为35.7m3/(s·m),水流均为滑行流。不同坡度断面比能、相对比能沿程变化见 图6、图7。
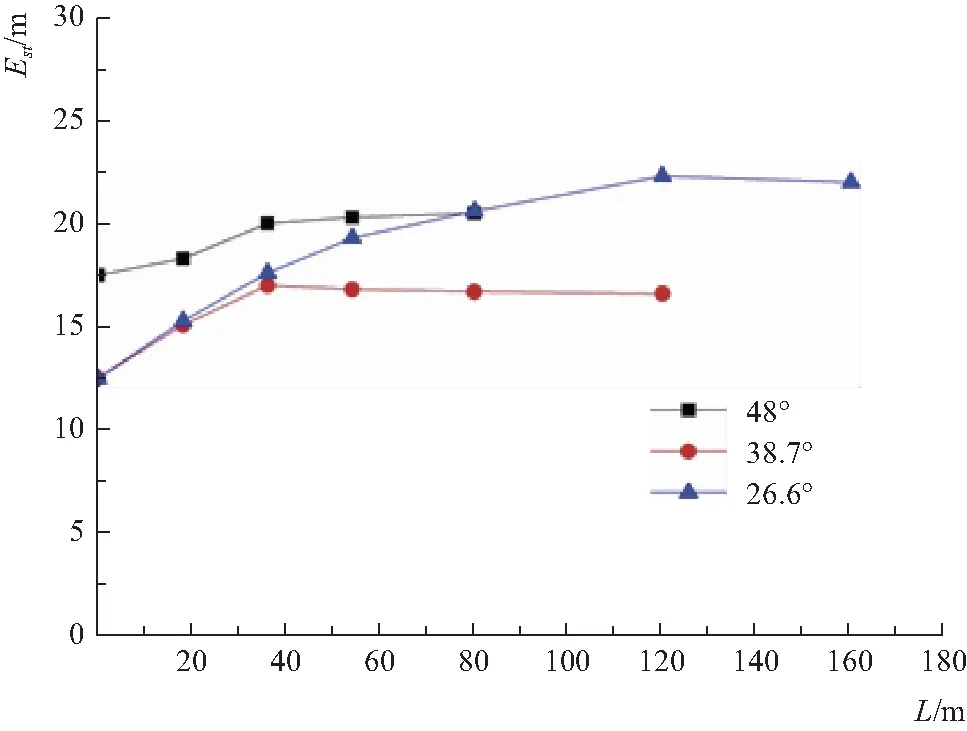
图6 不同坡度条件下断面比能与沿程关系比较

图7 不同坡度条件下相对比能与沿程关系比较
从图6中可以看出,不同坡度的台阶溢洪道断面比能均随流程增加先升高后平稳,但坡度间变化不规律,48.0°坡角断面比能平稳后介于38.7°与26.6°坡角之间;从图7中可以看出,不同坡度相对比能随流程呈线性变化,同流程长度断面处相对比能随角度增加而增加,说明增加台阶溢洪道坡角可以加大损耗水流能量。
4 水头损失分析
台阶溢洪道水头损失是由于各级台阶结构对水流产生局部水头损失,如“糙率”泄水槽,形成全流程中沿程水头损失规律。对比光滑溢洪道与台阶溢洪道对应位置处水头损失可知,可将台阶溢洪道水头损失hwt分为光滑溢洪道沿程损失hwg、台阶溢洪道高于光滑溢洪道水头损失部分ΔEs。则
hwt=hwg+ΔEs
(4)
光滑溢洪道沿程水头损失计算式为
(5)
台阶溢洪道超出光滑溢洪道水头损失部分即为相对比能,计算式与流程长度呈线性相关,即为
ΔEs=kL
(6)
其中,斜率k值与台阶尺寸、坡度有关。
根据不同台阶高度、单宽流量及坡度计算出相对比能,再对不同坡度、台阶高度下各工况斜率k值进行曲线拟合,得出经验性计算式:
(7)
式中θ——坡度,°;d——台阶高度,m。
式(7)与试验值间相关系数在0.995以上,结合计算式(4)、式(5)、式(6)、式(7)可得出计算台阶式溢洪道沿程水头损失经验计算式:
(8)
5 结 语
台阶溢洪道是集泄水与消能为一体的水利建筑,其优越的水利特性能够改变水流形态,提高溢洪道沿程的水头损失,完美结合了泄水与消能功能。利用已成熟的光滑溢洪道水力计算理论,将台阶溢洪道比能与光滑溢洪道比能作比较,通过相对比能概念,对台阶溢洪道进行试验分析,结果表明:台阶溢洪道超出光滑溢洪道的水头损失与台阶溢洪道相对比能相同;台阶溢洪道断面比能随流程长度先增加后平稳,而相对比能随流程长度呈线性递增,相关系数为0.9981~0.9997且与单宽流量无关;同一断面不同流量时,每级台阶对滑行水流产生的旋滚消能为定值。相对比能会随台阶高度增加而增加,等流程相对比能随坡角增大而增大。fffff8
[1] 秦广莉.台阶式溢洪道消能率影响因素分析[J].水利规划与设计,2016(2):49-51.
[2] 白雪莲,刘云贵.浅谈竖井式溢洪道设计计算[J].水利建设与管理,2016,36(6):21-24.
[3] 伍平,王波,陈云良,等.大落差多级阶梯泄槽水流稳定平衡态研究[J].水力发电学报,2013,32(2):190-194.
[4] 王莉艳.斯木塔斯水电站台阶式溢洪道消能设计[J].中国水能及电气化,2014(4):65-67.
[5] 文明宜,刘韩生,范灵芝.台阶式溢洪道水流比能与剩余能量关系研究[J].人民黄河,2016,38(4):82-84.
[6] 文明宜,刘韩生,范灵芝,等.台阶式溢洪道水流能量特性的研究[J].长江科学院院报,2016,33(7):60-62.

