基于流动和传热引起的熵产对螺旋板式换热器的多目标优化

李 闯 黄跃武



基于流动和传热引起的熵产对螺旋板式换热器的多目标优化

李 闯 黄跃武

（东华大学环境科学与工程学院 上海 201620）

应用遗传算法，在传热量一定的约束条件下，以螺旋板换热器尺寸参数为优化变量，流体的传热和阻力引起的熵产为目标函数，进行多目标优化，并得出pareto前沿图，最后对pareto前沿解域进行TOPSIS决策，选出最优解。然后对比多目标、单目标优化下，螺旋板换热器的换热面积和压降。结果表明，传热量不变的条件下，多目标优化相较于以压降熵产为单一目标的优化压降降低8.4%，换热面积减少58.3%；相较于以传热熵产为单一目标的优化，压降降低45.76%，换热面积减少25.5%。

螺旋式板式换热器；多目标优化；熵产；遗传算法

0 引言

螺旋板式换热器在生产中有广泛的用途，但在设计优化方面更多的是依靠经验，理论研究方面还不够深入，经常无法满足对于有特定需求的用户，也没有更有效的方案达到设计要求，因此在实际中，更多的是使用技术比较成熟的管壳式换热器。随着技术的发展，各种优化算法和计算机技术的成熟，换热器优化设计方面也有了突破性进展[1]。本文就是应用遗传算法和计算机强大的计算技术，对螺旋板式换热器进行传热和流体阻力综合性能的优化。

国内外文献中已有很多用于评价和指导这类优化问题的方法。比如Bejan[2]考虑到换热面积增大时，换热器效率增加，同时压降升高，于是定义了最小熵产法作为评价强化换热技术的准则。左丹等通过分析相关原理，建立了螺旋板式换热器的数学物理模型，对特定型号的螺旋板换热器做了模拟计算，得到了螺旋板换热器螺旋通道中流体温度分布、压力分布图，以及传热特性和流动阻力分布情况，最后进行了相关实验来验证模拟的合理性。熊大曦[3]等研究了换热器的效能与熵产的关系，在进出口温度均匀不变的条件下，熵产数随着效能的增加而逐渐减小，并且效能和熵产数是一一对应的，效能与熵产数一样，都表示了换热器系统中热力学第二定律的完善程度。蔡飞[4]等利用遗传算法和多目标优化，以传热和压降引起的火积耗散数最小为目标，对螺旋板换热器流体出口温度以及冷、热流体的流速的不同组合做了多目标优化。施志钢等[5]以地埋管运行过程中最小熵产为目标，综合考虑传热性能和消耗的功率以及埋管支路间热短路影响，建立管内载能流体的熵产模型，提出了地埋管换热器的优化设计模型，从根本上提高了系统性能，减少了不可逆损失。

遗传算法作为一种高度并行随机全局搜索方法，通过代表整个解集的种群进化，以内在并行的方式搜索多个非劣解，决策者可以在多个解中选择决策方案[6]。本文以换热量为约束条件，优化换热器结构参数，利用遗传算法计算两个相互矛盾的目标函数——传热熵产及压降熵产，最后在大范围解域中搜寻最优的设计结果区间构成pareto前沿，并利用TOPSISI决策方法在目标函数最优解域中产生换热器的最优解[7]。最后同单目标优化进行对比，研究在螺旋板式换热器优化设计中不同方法的优劣。

1 螺旋板式换热器模型

基本结构：螺旋板式换热器主要是由两张长而薄的钢板平行放置，经过卷板机卷制成螺旋形，两张长钢板之间需要焊上定距柱或其他用来保持两板之间产生一定距离的阻隔物，这个间距就是换热通道，定距柱也用来支撑钢板抵抗换热过程中流体的压力，并且可以增加流体在流道中流动时的瑞流程度从而提高换热效率。当换热两流体经过相邻的间隙时，通过薄钢板进行传热，螺旋形的通道有效的增加了流体流过的路程增加了换热，并且体积较小。螺旋板式换热器有很多种，如图1是一种可拆式螺旋板式换热气模型。螺旋板式换热器内换热工质可以是液-气，液-液，气-气，本文讨论液-液无相变工况。

图1 一种可拆式螺旋板式换热器模型

1.1 热力学模型

螺旋板式换热器的相关计算，文献[8]中已给出公式。

根据流体的热力学平衡可以得出：

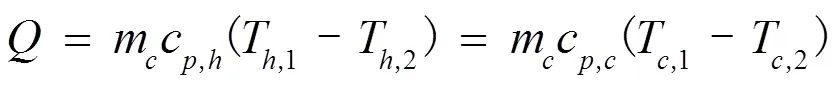
式中，、、分别表示质量流量、比定压热容、温度，下角标、表示冷、热流体。

换热器总换热面积：=2××（2）

传热单元数：

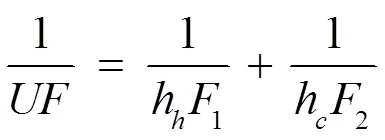
冷流体出口温度：

政府部门要进一步加强土地流转、征用宣传动员工作，严格按照相关规定及时足额兑现被流转、征用土地群众的各项补偿和扶持政策。对新规划工程应制定多个比选方案，项目选址应先广泛征求项目区村、组及土地使用管理权持有者的意愿，提高方案的可操作性，确保工程实施顺利。

热流体出口温度：

热流体侧给热系数：

冷流体侧给热系数：

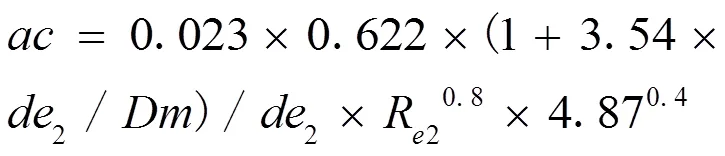
流通截面积：1=×（11）

螺旋板有效换热长度：

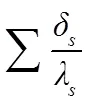
本算例中设定流体物性参数如表1所示。

表1 冷热流体设计参数

1.2 水力模型

流体阻力计算：

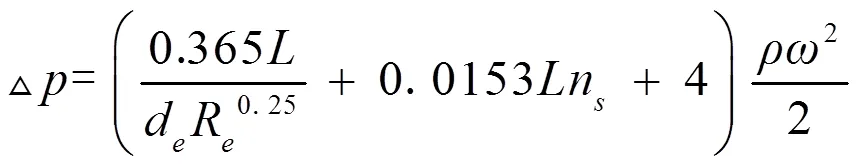
上式适用于雷诺数R=5000-44000，n=116-232。

式中，为换热器螺旋通道长度，m；n为定距柱密度，这里取181个/㎡；为流体密度；为流体速度，m/s；d为螺旋通道当量直径，m。

2 多目标优化

工程上很多优化问题是相互冲突的多个目标组成，因此多目标优化是在多个目标中寻求最佳平衡点。在优化传热单元或传热系统时，有一个普遍的现象，研究者经常把一些目标函数拟合成单一的目标函数来进行整体性能的评估，例如效用理论、加权和方法等。多目标优化中，由于各目标之间很难同时达到最优，所以多目标优化常常产生一系列有效解，也叫做Pareto解[10]，多目标优化是来确定整个pareto最优解集的广义的方法[11]。

2.1 多目标适值函数

熵产被认为是任意不可逆过程不可逆性的度量[12]。换热器存在两个方面的不可逆性，一个是冷热流体换热不可逆，另一个是冷热流体流动时阻力导致压降的不可逆性。本文将两个方面的不可逆损失分别以熵产形式表示出，即传热熵产和压力熵产，分别如下[13]：

传热熵产：

式中，m为热流体质量流速，kg/s；c为热流体的比热容，J/kg·K；T、T为热流体进出口温度，K；m为冷流体质量流速，kg/s；c为冷流体的比热容，J/kg·K；T、T为冷流体进出口温度，K。

压力熵产：

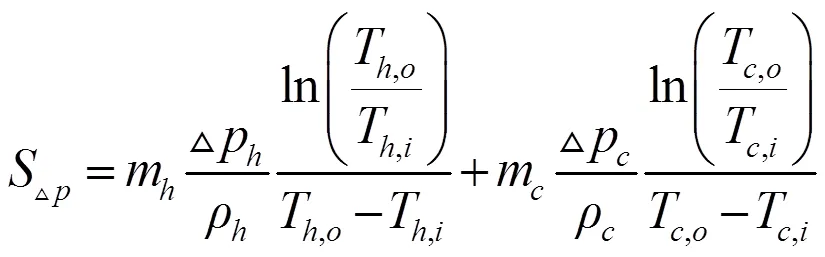
式中，Δp、Δp为热冷流体侧压降，Pa；、为热冷流体密度，kg/m3。

总熵产的计算公式：

=S+Δρ（20）

2.2 决策及最优解的选取

由遗传算法得出的pareto前沿，是一个解域，并不能得出最终结果，需要一个决策以便在所得的最优解域中选择出最终设计参数[4]。对于本文的螺旋板式换热器，利用TOPSIS决策方法[14]来最终确定设计参数。相关计算公式如下：

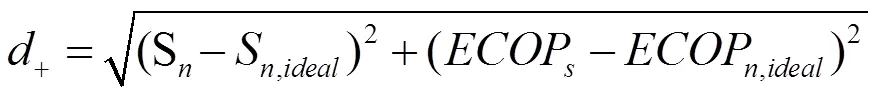
其中，S、ECOP分别是pareto前沿上的点的横纵坐标；Snon，ECOPnon分别是最不理想点横纵坐标；S，ECOP分别是理想点横纵坐标；+，-分别是pareto前沿上的点到最理想点以及最不理想点的距离。TOPSIS评判准则即使pareto前沿上的点到最理想点的距离越近越好，到最不理想点的距离越远越好[15]。

2.3 换热器主要设计参数取值范围

螺旋板换热器主要设计参数以及本文中与相关参数变化相关的参数作为设计变量列在表2中，表中已列出其约束范围。

表2 螺旋板换热器主要设计参数

3 结果与分析

运用MATLAB进行遗传算法模拟计算。计算后得出的图2为未修正的传热熵产和压力熵产构成的pareto前沿图，这些解集构成了一条曲线，图像显示压力熵产和传热熵产的变化，当一个量得到优化时，另一个量向劣势变化。

图2 最小熵产数所得到的pareto前沿

从图2可以看出传热熵产和压力熵产在数值上相差较大，所以不能直接找到最优解点，需要将所得数值进行归一化，建立归一化之后目标函数映射为（0-1）之间的数进行分布，如图3所示。最后选择TOPSIS决策方法选择最终的优化解。其中理想点是（0，0）点，最不理想点是（1，1）。

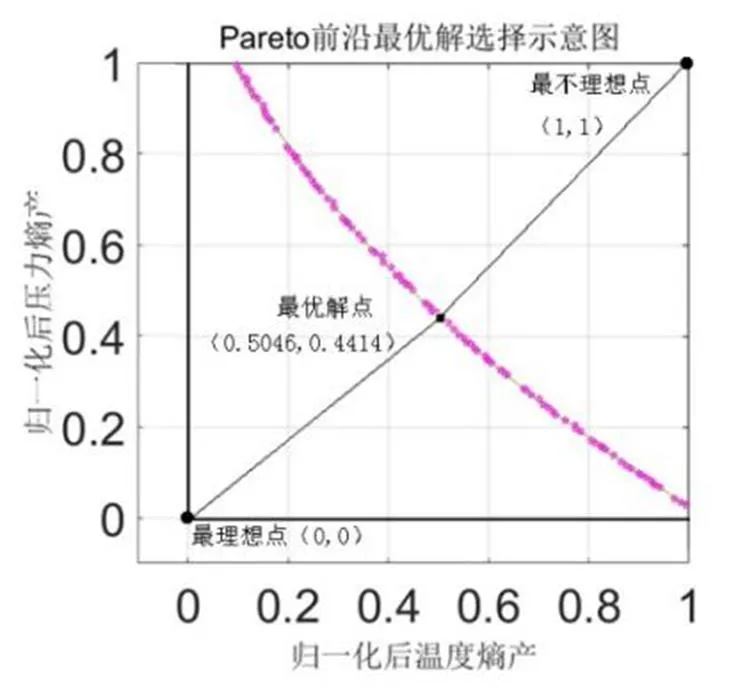
图3 压力、传热熵产归一化之后pareto前沿上最优解选择示意图

在进行TOPSIS决策时，本文利用MATLAB自带GA工具箱中函数拟合工具，根据图3拟合出曲线函数（24），然后根据式（21）-（23）可以计算出归一化pareto图上的最优解点（0.5046，0.4414），并找到该点所对应换热器的各项性能参数。

=-0.511×3+1.3825×2-2.02×+1.1721 （24）

为了显示多目标和单目标优化的不同，本课题还进行了单目标计算，分别以压力熵产和传热熵产为单目标进行计算，结果列于表3。

表3 换热量一定时多目标和单目标优化结果对比

通过表3可以看出，在保持换热量不变时，多目标优化中的压降和换热面积都是最小，相比压降单目标优化压降最大降低8.4%，换热面积最大减少58.3%；相比温度单目标优化压降最大降低45.76%，换热面积最大减少25.5%。

表3显示，以传热熵产为单目标时，总熵产最小，但是对应的压降、传热面积相对多目标优化得到的压降和传热面积较大，所以以传热熵产为单目标进行优化时，尽管熵产最小，但并不能使换热面积和压降最低，因为单独以传热熵产为目标进行优化时，会导致压力熵产较大。由表3可以看出，以传热熵产为单目标的优化，压力熵产比多目标优化高46.12%，传热熵产比多目标优化低75.14%，可见压力熵产对结果的影响比传热熵产对结果的影响要大。

最终结果显示无论是以传热熵产为单目标的优化，还是以压力熵产为单目标的优化，最终得到的压降、换热面积都比多目标优化的要大。所以对于螺旋板式换热器，在换热量一定的条件下，多目标优化对于降低压降和减小换热面积更有利。

4 结论

（1）基于流动和传热引起的熵产对螺旋板式换热器的多目标优化，传热熵产远大于压力熵产，利用TOPSIS决策选择最优解时需进行归一化处理。

（2）在控制换热量不变的条件下，对螺旋板式换热器的多目标优化研究表明，压力熵产对换热器压降和换热面积大小的影响比传热熵产要大。

（3）对螺旋板式换热器进行多目标优化，换热面积和压降比以压力熵产和传热熵产为单一目标进行优化时要小，所以在换热量一定的条件下，多目标优化对于降低换热器压降和减小换热面积更有利。

[1] YIN H, OOKA R. Shape optimization of water-to-water plate-fin heat exchanger using computational fluid dynamics and genetic algorithm[J]. Applied Thermal Engineering, 2015,80:310-318.

[2] Bejan A. Entropy Generation Through Heat and Fluid Flow[M]. New York: Wiley&Sons, 1982:119-134.

[3] 熊大曦,李志信,过增元.换热器的效能与熵产分析[J].工程热物理学报,1997,18(1):90-94.

[4] 蔡飞,吴吁生.基于耗散理论的螺旋板式换热器多目标优化设计[J].电力与能源,2013,34(1)24-26.

[5] 施志钢,胡松.基于最小熵产的地埋管换热器优化设计研究[J].太阳能学报,2015,36(3):587-592.

[6] 赵亮,雎刚,吕剑虹.一种改进的遗传多目标优化算法及其应用[J].中国电机工程学报,2008,28(2):96-102.

[7] 王哲,厉彦忠.板翅式换热器传热阻力多目标权衡优化[J].工程热物理学报,2016,37(2):399-404.

[8] 兰州石油机械研究所.换热器（第二版）[M].北京:中国石化出版社,2013:1015-1028.

[9] XueTao Cheng, XinGang Liang.Discussion on the applicability of entropy generation minimization and entransy theory to the evaluation of thermodynamic performance for heat pump systems[J].Energy Conversion and Management, 2014,80:238-242.

[10] 姜衡,管贻生.基于响应面法的立式加工中心动静态多目标优化[J].机械工程学报,2011,47(11):125-133.

[11] Ya Ge, Zhichun Liu, Wei Liu. Multi-objective genetic optimization of the heat transfer for tube inserted with porous media[J]. International Journal of Heat and Mass Transfer, 2016,101:981-987.

[12] 陈群,吴晶.换热器组传热性能的优化原理比较[J].科学通报,2011,56(1):82-87.

[13] M Mishra, PK Das, S Sarangi. Second law based optimisation of crossflow plate-fin heat exchanger designusing genetic algorithm[J]. Applied Thermal Engineering, 2009,29(14-15):2983-2989.

[14] MH Ahmadi, MA Ahmadi. Multi objective optimization of performance of three-heat-source irreversible refrigerators based algorithm NSGAII[J]. Renewable and Sustainable Energy Reviews, 2016,60:784-794.

[15] Hoseyn S, Reza M. Efficiency enhancement of a gas turbine cycle using an optimized tubular recuperative heat exchanger[J]. HoseynSayyaadi&Reza Mehrabipour, 2012, 38:362-375.

Multi-optimization of the Spiral Plate Heat ExchangerBased on the Entropy ProductionCaused by Flow and Heat Transfer

Li Chuang Huang Yuewu

( Donghua University, Shanghai, 201620 )

In this paper, by using the genetic algorithm, on the constraint conditions of the heat transfer, structural parameters of spiral plate heat exchanger as optimization variables, the entropy productions caused by heat transfer and resistance of the fluid as the objective function, the multi-objective optimization, it is concluded that the pareto frontier graph. TOPSIS was carried out on the pareto frontier solution domain decision, choosing the optimal solution.Then using the single target of heat transfer enropy production and resistance entopy production optimize the heat exchanger, comparing spiral plate heat exchanger heat transfer area and the pressure drop with the results of multiobjective optimizition. Results show that under the constant heat transmission, the multiobjective optimization results compared with single objective optimization result of the entropy production of pressure drop, pressure drop decreases by 8.4%, the heat exchange area decreases by 58.3%; Compared with single objective optimization result of entropy production of heat transfer, pressure decreases by 45.76%, the heat exchange area decreases by 25.5%.

The spiral plate heat exchanger; multi-objective optimization; entropy generation; genetic algorithm

1671-6612（2017）06-555-06

TK124/TK172

A

李 闯（1990-），男，硕士，E-mail：lichuangpyh@163.com

黄跃武（1972-），男，博士，教授，E-mail：huangyuewu@dhu.edu.cn

2017-04-08