反应−效应相容性范式下不同数字表征方式和身体经验对数字认知加工的影响*
(陕西师范大学心理学院;陕西省行为与认知神经科学重点实验室,西安 710062)
1 前言
数量作为一种抽象概念,在幼儿学习的初始多采用木棒、珠子、手指等实物来代替。关于数量表征的研究不仅对揭示数学能力的心理机制具有理论意义,而且对儿童数学运算能力的培养具有现实指导作用(杨志艳,周欣,2015)。根据进化学的观点,数量表征可分为非符号的数量表征和符号的数量表征(Bonny &Lourenco,2013)。Imbo,Vandierendonck和Fias (2011)认为,在儿童尚未习得符号的数量表征方式时,会采用手指数数策略来解决简单算术问题。手指数字表征是在基于自身感知与运动经验的基础上使用手指来表征数量,该表征与其它数量表征方式之间存在本质的差异,这些差异影响与数量表征无关的阿拉伯数字大小比较任务(Klein,Moeller,Willmes,Nuerk,&Domahs,2011),如在非符号加法任务和大小比较任务中激活手指表征相关的脑区,而在符号数字任务中则没有激活(Krinzinger et al.,2011),这表明手指数字表征在非符号表征向符号表征的转换过程中起到某种作用。有研究表明成人在简单运算时,也会受到手指数字表征的影响(Klein et al.,2011;Badets,Pesenti,&Olivier,2010);并且与手指表征相关的脑区是成人完成计算任务的生理基础(Andres,Michaux,&Pesenti,2012)。因此,手指对于数字认知具有促进作用(Fischer,Kaufmann,&Domahs,2012),对于数学能力发展的预测作用也意义重大。但是,关于手指数字表征是否是一种数字语义的表征方式尚缺乏直接有力的证据,身体经验在数字表征中的作用也尚待进一步深入探讨。
根据用手习惯的不同,手指数字表征可分为两种(Di Luca,Lefèvre,&Pesenti,2010),一种是标准的手指组合,是所在文化背景下的一种约定俗成的手指数字表征方式,人们按照固定的顺序依次伸出手指来表征数字或者按照某种固定的方式表征数字;另一种是非标准的手指组合,相对于标准的手指组合,它是一种不常用的手指数字表征方式。儿童在发展早期就会习得这两种手指数字表征方式,这可能有助于儿童形成数字符号概念(Krinzinger et al.,2011)。在文化背景下产生的这两种手指表征方式,不仅表现为形体上的差异,而且对数字认知的影响也存在差异。标准的手指数字表征符合个体的手指计数习惯,从而作为象征性的符号与其语义产生直接联结,可自动获得数字语义,但是非标准的表征则不能(Di Luca et al.,2010)。Di Luca等(2010)的研究表明标准的手指数字表征似乎作为一种符号表示方法与数字语义之间存在直接的联系。Domahs,Moeller,Huber,Willmes和 Nuerk (2010)认为德国人的手指数字表征方式是 5进制(sub-basefive),即用手指来表征数字是以每只手的5根手指为一个单位,逢 5进1;并且这种 5进制的手指数字表征方式会对阿拉伯数字的大小加工产生影响。随后,Klein等(2011)又对朝鲜聋哑人的手指表征方式进行了研究,发现其表征方式与其他文化背景下的表征方式不同,具体表现为在用手指表征不同的数字时手指的指向会发生变化,而该差异会影响阿拉伯数字大小的比较。这说明不同文化背景下产生的手指数字表征体系的差异,对数字认知加工的影响是不同的。中国人的手指数字表征方式有其特殊性,尤其表现在较大数字的数字表征时仅用一只手就可表示,但目前对中国人手指表征方式的研究较少。因此,手指与数字之间关系研究的本土化,探讨手指在中国人数字认知中的作用具有重要意义(Bender &Beller,2011)。
反应−效应(Response - Effect,R-E)相容性是指对未来反应结果的预期所引起的对当前反应的促进或干扰效应(Kunde,2001,2003;Hubbard,Gazzaley,&Morsella,2011;Pfister &Kunde,2013,Pfister,Dolk,Prinz,&Kunde,2014),具体来说,是指刺激所引发的反应反复与某一给定的结果(效应)相连接一段时间后,被试会产生对反应结果的预期,尽管动作效应发生在动作执行之后,但相比较不相容条件,相容条件下的被试反应更快(Gaschler &Nattkemper,2012;Yun &Proctor,2012;Pfister et al.,2014),即与被试期望一致的结果(相容匹配)会促进对刺激的反应。应当指出的是,预测感知事件取决于如下条件,即只有当被试被明确要求产生该效应时才能观察到可靠的R-E相容性效应;如果效应为任务无关因素,则不会出现R-E相容性效应(Ansorge,2002)。如Janczyk,Pfister和Kunde (2012)发现只有相匹配的效应显著且任务相关时,才能观察到预期的影响。该研究范式最早由Kunde (2001)提出,目的是为支持观念运动理论(Ideamotor theory)。幼儿运用手指计数策略去解决数学问题时,手指呈现出计算结果显示了该计算过程的感知−运动输出。幼儿通过多次的练习,手指配置及其表征将会逐渐与数学问题及结果相联结,进而影响数学问题的解决,此结果与观念运动理论的预期一致。
观念运动理论认为,个体根据行为的感知效果来选择动作(James,1890)。该选择过程包含两个阶段:首先,习得动作及其随后的感知效果之间的联结,即动作−效果联结(Action-effect bindings);然后,反向运用这一联结,通过对动作效果的预期,自动激活相应的动作(孙月,陈巍,丁峻,2011)。大量实证研究采用 R-E相容性范式均支持了观念运动理论:Kunde (2001,2003)采用按键反应在视觉和听觉刺激以及持续时长等知觉层面均发现了 R-E相容性效应,即效应与反应相容时会促进个体反应绩效的提高;Hommel,Alonso和Fuentes (2003)探讨了语词概念的R-E相容性,结果发现当测试阶段与学习阶段的语词存在语义上的连接时,被试表现更好。那么在数字认知加工中是否也存在R-E相容性效应,以及反应与预期相容时是否也会导致数字认知加工绩效的提高?Badets等(2010)以成人被试为研究对象,采用R-E相容性范式试图探讨手指配置在简单数学运算中的作用,研究发现手指与数字之间的联结可以自动激活反应的产生,在实验中表现为由手指所表征的数字作为语音反应之后的效应,当效应与反应相容时被试反应更快,这在一定程度上也证实了数字认知领域R-E相容性效应的存在。
在Badets等(2010)的研究中,实验刺激为两类简单的加法算式,一类为结果是单手表示的(如:1+2),一类为结果需双手表示(如:3+4),要求被试口头作答,被试反应后的正确(实验 1,相容条件)或错误答案(实验 2,不相容条件)以手指或木棒的形式呈现。由于手指所表征的数字作为语音反应之后的效应,当效应与反应相容时被试反应更快,结果支持了 R-E相容性在数字认知加工中的优势效应,但其研究所采用的手指−数字表征体系本身存在两方面的问题:一方面是包含了数量大小与手指多少的相容性问题,即表征较大数字需要双手手指/较多木棒,而表征较小数字需单手手指/较少木棒。这种表征方式本身包含了感知层面上近似的“多少”的数量感知,而不仅仅是精确的数字语义内涵。因此,这种手指的多少与数字大小之间的相容性所导致的感知层面的维度重合并不能严谨地论证手指数字表征与具体数字之间的语义联结。另一方面,其研究所采用的这种刺激−反应−效应(S-R-E)序列,不仅包含了反应与效应的相容性,也存在刺激与效应的相容性,如刺激“2+5”,效应是“2根手指与 5根手指”或“2根木棒与5根木棒”的组合,这种刺激与效应之间的相容性也可能影响到实验结果。中国人的手指数字表征方式,仅一只手就可以表征 10以内的所有数字,尤其对于较大数字(以 4为分界点)而言避免了数字大小与表征方式的手指多少的对应关系,在一定程度上可以排除“手指多少与数字大小”之间的感知层面关联所造成的影响,而且单手表示也可排除刺激和效应之间的相容性问题。中国人的手指数字表征方式与其他国家不同,有其特殊的文化内涵。因此手指与数字之间关系研究的本土化,探讨手指在中国人数字认知中的作用具有重要意义(Bender &Beller,2011;胡艳蓉,张丽,陈敏,2014)。Di Luca等(2010)的研究表明手指表征习惯在一定程度上也会影响到手指与数字的交互作用。那么手指−数字表征是否也存在R-E相容性效应从而有助于提高其反应绩效呢?R-E相容性效应是否受个体的手指表征习惯的影响以及这种影响产生的效果如何?
为了回答上述问题,本研究拟采用R-E相容性的研究范式,通过设置不同的数字表征方式来考察数概念层面上R-E相容性现象的存在及身体(手指)在其中的作用,探讨手指与数字之间的联结是否可以自动激活反应的产生以及手指数字表征习惯对数字认知加工的影响。实验1首先从知觉层面使用木棒表征的数字作为随后的效应,以验证语音反应方式下数学运算中R-E相容性的存在;实验2采用累计手指数字表征(胡艳蓉等,2014;Domahs et al.,2010)作为反应之后的效应,旨在考察手指数字表征与数字语义之间的联结,同时与实验1进行对比以考察手指数字表征的优势效应。实验3则采用中国人的手指数字表征,进一步排除反应与效应在知觉层面的相容性对结果的影响,从语义层面上考察手指数字表征与数字语义之间的联结,并为两种手指数字表征体系的比较提供理论支持。
2 实验1
实验1采用R-E相容性范式,并以一些木棒的组合为实验材料来表征数字(如图1所示),从知觉层面考察数学运算中是否存在R-E相容性效应。
2.1 方法
2.1.1 被试
30名大学生参加本实验,其中女生 22名,年龄18~22岁,平均年龄20.50岁。视力或矫正视力正常,无色盲或色弱,此前均未参加过类似的实验。
2.1.2 仪器和材料
实验程序采用E-prime 2.0编制,在Lenovo计算机上运行,刺激呈现在屏幕背景为黑色的 17英寸的液晶显示器上(分辨率为 1024×768,刷新频率为60 Hz)。被试的语音反应通过串口反应盒(Serial Response Box)和外接麦克风设备进行采集。
实验中所用刺激包括简单的加法运算,分为较小问题(0+2,1+1,0+3,1+2)和较大问题(2+5,3+4,3+5,4+4),用阿拉伯数字表示,字体为Times New Roman,96号字,前景是灰色,背景是黑色。效应用灰色的木棒(高 10 cm,宽 1 cm)组合表示,如图1所示,大于 5的组合又分为左右两组,目的是为了与实验2的手指数字表征方式的匹配,否则可能会导致被试辨认难度的增加,并且不利于两个实验之间的比较。

图1 累计木棒表征的数字(Badets et al.,2010)
2.1.3 实验程序
实验程序包含练习阶段和正式实验两部分。共16次练习,目的在于让被试了解实验程序及反应方式。正式实验包括相容和不相容两个组块,每一组块均是相同的8个加法运算,每个算式随机呈现10次,共160次。整个实验持续时间大约10 min,实验中间设置一次休息时间。如图2所示,具体的实验程序如下:先呈现一个简单的加法运算,被试应在1500 ms时间内口头报告得数,被试进行语音反应后随即呈现效应(800 ms),即木棒表征的数字。两个试次之间的时间间隔是1500 ms。
本实验采用单因素的被试内设计,自变量是相容性(反应与其随后的效应之间的关系),分为相容(例如:刺激是1+2,口头报告3,随即呈现效应是3根木棒)和不相容(例如:刺激是 1+2,口头报告 3,随即呈现效应是 5根木棒)两种条件。一组被试先进行相容任务,再不相容任务;另一组被试对组块顺序进行平衡,先不相容任务,再相容任务。因变量是对简单加法运算进行计算并口头报告答案的反应时和正确率。

图2 实验流程图
2.2 结果与讨论
计算被试口头报告的反应时和正确率作为统计指标。用SPSS 20.0进行数据处理,首先剔除了反应时在±3个标准差之外的试次(2.30%),3个实验中反应时结果如表1所示,由于任务比较简单,正确率均在 99%以上,且分析结果均不显著。实验 2和3亦是如此,故之后不再对正确率进行分析。且先前采用语音反应方式的研究(Badets et al.,2010;Koch &Kunde,2002)均未对正确率进行分析。

表1 三个实验中相容和不相容条件的反应时及效应量(M ± SD)
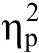
实验1首先从知觉层面证实了数学运算中R-E相容性效应的存在,但本实验中所使用的材料是木棒,作为一种简单的计数器,在幼儿数学学习中使用类似的代替物较多。除了这些用于计数的客体材料外,手指也是一种重要的计数工具,尤其是十以内的加减运算。那么用手指表征数字这种方式是否也存在 R-E相容性效应?并且作为主体一部分的手指与客体材料木棒之间是否存在差异?此外,手指数数这种简单的数学计算方式大都是幼儿初学数字时所常采用的,那么成年人是否会受到手指计数的影响?基于此,实验2采用累计手指的数字表征方式继续对上述问题进行探讨。
3 实验2
本实验旨在考察采用手指来表征语音反应之后的数字是否仍存在R-E相容性效应。累计手指的数字表征方式(如图3所示)与木棒表征数字的方式类似,即“X根手指或木棒表征数字 X” (10以内),这种表征方式排除了数字表征的难度差异所造成的影响,便于实验之间的比较。本实验验证如下假设:(1)基于手指−数字的表征存在R-E相容性效应;(2)相比较木棒表征数字的方式,手指数字表征更有优势。
3.1 方法
3.1.1 被试
30名大学生参加本实验,女生 20名,年龄19~22岁,平均年龄 20.25岁。视力或矫正视力正常,无色盲或色弱,此前均未参加过类似的实验。
3.1.2 实验材料与程序
如图3所示,除了反应之后的效应由木棒改为手指外,实验2的程序与实验1基本一致。
3.2 结果与讨论

实验2中表征数字的方式与实验1类似,均是“X根手指或木棒表征数字X”。这种表征方式本身也存在一个问题,即较大数字的手势更复杂,而较小数字的手势更简单。人类与动物共同拥有两种离散量表征系统,即小数的精确表征系统和大数的近似表征系统,其分界点为4 (牛玉柏,时冉冉,曹贤才,2016)。所以,被试可能采取先天就有的“近似数量表征系统”对大数字进行模糊的数量多少的感知,而无须进行精确的数字语义加工即可判断效应是否相容。因此,这种表征方式本身的复杂程度也可能是产生R-E相容性效应的原因,而非手指所表征的数字意义。此外,在这两种表征方式的刺激−反应−效应(S-R-E)的序列中,当反应与效应相容时刺激与效应也是相容的,如刺激“2+5”,效应是“2根手指加 5根手指”或“2根木棒加 5根木棒”的组合,这种刺激与效应之间的相容性也可能影响到实验的结果。即所谓标准的数字表征体系问题,Badets等(2010)的研究所采用的手指数字表征对参与实验的被试群体是标准的数字表征体系,而对于本实验群体却未必如此。关于手指数字的表征方式,中国人另有一套体系,如图4所示。这种表征方式一方面于被试群体而言更为熟悉,属于标准的手指数字表征,另一方面可以规避较大数字的近似数量表征系统影响。因此,实验3选用中国人的手指数字表征方式,进一步排除感知层面的近似数量表征所造成的干扰,考察手指数字表征与数字的精确语义联结。

图3 累计手指表征的数字(Badets et al.,2010)
4 实验3
本实验旨在探索在排除了近似数量表征系统以及刺激−效应相容等干扰因素时,是否存在 R-E相容性效应,进一步证明手指数字表征与数字的语义联结。因为实验2中的手指数字表征方式是一种根据加法原则逐渐累计的方式,对于较大的数字其表征方式本身也更为复杂;而中国人的手指数字表征方式,尤其是大于5的数字的表征(从图4可以看出对于数字6和8,仅需2根手指就可以表征,甚至数字 9仅需一根手指就可以进行表征),一方面排除了表征数字大小与手指的多少之间对应关系的影响,从而更为纯粹地验证手指与数字之间精确的语义联结的R-E相容性;另一方面这种更符合中国被试群体经验的表征方式,也为不同的手势体系之间的比较提供数据支持。本实验所采用的中国人的手指数字表征方式来源于个人生活经验,同时在维基百科和 Domahs等(2010)的研究以及本实验的被试中也得到了验证。
4.1 方法
4.1.1 被试
30名大学生参加本实验,女生 24名,年龄19~22岁,平均年龄20.5岁。视力或矫正视力正常,无色盲或色弱,此前均未参加过类似的实验。
4.1.2 实验材料与程序
实验3的程序与实验1基本相同,所不同的是反应之后的效应改用中国人的手指数字表征方式来代替,如图4所示。
4.2 结果与讨论


图4 中国人手指数字表征方式

5 总讨论
5.1 R-E 相容性对数字认知加工的影响
观念运动理论认为,即使与反应相关联的感知结果出现在反应之后,它也可影响反应的进行。本研究基于R-E相容性范式,通过设置不同的数字表征方式以考察数概念层面上 R-E相容性效应的存在及其数字表征方式及身体经验对数字认知加工的影响。实验 1采用知觉层面上木棒表征的数字,以考察语音反应方式下数概念上 R-E相容性的存在;实验2在实验1的基础上采用知觉和语义层面上累积手指表征的数字作为反应之后的效应,旨在探讨手指数字表征中 R-E相容性的匹配优势对数字认知加工的影响;实验3则进一步采用中国人特有的手指数字表征,以期进一步排除上述实验中感知层面上近似数量表征系统的影响,考察纯粹语义概念层面上手指数字表征与数字语义内涵的直接关联及其对数字认知加工的影响。
实验1采用纯粹知觉层面上木棒数字表征,得到了接近显著的R-E相容性效应,实验2和实验3则用不同形式的手指数字表征均表现出显著的R-E相容性效应,表明反应之后的效应与之前反应相容时会对当前反应产生影响,验证了基于数字表征的R-E相容性效应的存在,支持了观念运动理论,说明除了当刺激与反应存在共同的感知维度(如空间位置、声音强度和持续时间等)会促进反应绩效的提高外,反应和效应之间的共同感知维度也会促进反应绩效的提高。具体在数字认知加工任务中,反应与效应无论在知觉层面还是语义层面的相容均会自动激活反应的产生,且身体(手指)在其中起一定作用,不同手指数字表征习惯对数字认知加工也会产生一定影响。在深层的概念水平上也存在R-E相容性效应,这表明预期表象在概念和知觉层面上都得到了加工。
以往基于短时训练所得到的 R-E相容性效应,多采用的是一些在实验室情境中获得的S-R-E的无意义联结,其生态效度受到局限。而在长时记忆基础上的 R-E相容性效应不仅可以考察教育及学习的作用,而且可以探索存储在长时记忆中的 S-R-E的联结对认知加工的影响,从而澄清其背后的认知加工机制。而本研究旨在考察基于长时人生经验的成人个体数字表征的R-E相容性现象(Badets et al.,2010),本研究采用Badets等(2010)的研究范式进一步考察基于人生经验的数字表征的 R-E相容性现象,以更深入地为观念运动理论提供实证支持。
然而,实验1和实验2的数字表征方式的性质相同,即“X根手指代表数字X”的逐渐累加的特点,这直接导致了在感知层面上对大数字的表征比小数字的表征更复杂,个体对较大数字的加工可能采用先天的近似数量表征系统,而非后天习得的精确的数字语义内涵。这种反应与效应之间在感知觉层面上的复杂程度的一致性与否,也可能是产生 R-E相容性的因素,而不仅仅是手指数字表征与数字语义之间的联结。实验3所采用的手指数字表征方式则在一定程度上避免了这种可能性,尤其是对于较大数字而言,如数字 8,仅伸出两根手指就可以表征,这与数字2的表征甚至在感知层面上存在某种重叠。然而,实验3的结果仍然表现出在相容条件下反应更快的现象,并且在单独考察较大数字时仍然存在R-E相容性效应,更进一步证实了标准的手指数字表征可以直接激活数字语义内涵的观点。
5.2 手指数字表征在R-E相容性匹配中的优势
在探讨主体材料(手指)与客体材料(木棒)表征数字的差异时,我们发现实验2和实验3的效应均优于实验 1,也就是说手指表征数字的方式优于木棒表征数字的方式。具体表现为在相容条件下,手指数字表征具有更大的促进效应,而在不相容条件下差异不显著。根据具身认知的观点,手指作为身体的一部分其对认知加工的影响深远。Domahs等(2010)进行的一项跨文化研究,选用德国聋人、德国和中国普通成年人3组被试,在阿拉伯数字比较任务中考察基于手指的五进制效应,探讨手指计数系统的结构对符号数字加工的影响。结果表明在所有组中均得到五进制效应,由此认为看似抽象的认知至少部分地根植于我们的身体经验,身体经验(即手指计数)影响成年人的抽象心理数字表征的结果。此外,Bloechle,Huber和Moeller (2015)关于两位数的大小比较任务的研究中,发现手指朝向十位数字方位的偏转,并且在个位−十位(UD)不相容的数字对中偏转减小。Bloechle等(2015)将此解释为身体经验对数字加工的影响。本研究中两种手指数字表征方式均优于木棒表征数字的方式,这一点也说明了手指作为主体的一部分与客体材料相比较对认知加工的影响是不同的,为具身数量的观点提供进一步的支持。
实验3所采用的手指数字表征体系,是中国人较为通用的表征方法。一方面排除感知层面上近似数量表征系统的影响,纯粹考察语义概念层面上手指数字表征与数字语义内涵的直接关联;另一方面也可对手指数字表征的跨文化研究提供补充。结果表明在这种中国特有的数字表征方式下也存在R-E相容性效应,同时也表明仅语义概念层面的关联也可产生R-E相容性效应。此外,先前的研究表明手指的表征习惯会影响到多种数学加工任务 (Di Luca et al.,2010)。也就是说,相比较非标准的手指数数体系,标准的手指数字表征(即个体习惯或习得的)反应更快更好。根据前人的研究结果,实验3所用表征体系对反应的促进效应相较于实验2应该更为明显(Di Luca &Pesenti,2011;胡艳蓉等,2014)。然而,数据处理结果表明无论是相容还是不相容条件,两种手势体系的反应时均无显著差异,也就是说实验3中的手指表征优势并没有体现出来。其原因可能有如下几点:首先,R-E效应相容性,最初是在知觉层面发现的,实验2的数字表征方式既包含知觉层面又包含概念层面,这种双重加工的优势更为显著;并且知觉层面的加工,相比较概念层面(尤其是数理概念)的加工更为快捷,由此掩盖了实验 3手指表征方式的优势;其次,在儿童学习的数字或基本的算术运算时多采用手指数数策略以列举事物,这与实验 2的数字表征方式的是一致的,是我们学习数数甚至数学的最初始基础的方式,影响深远(Badets et al.,2010;Andres et al.,2012);最后,在加法计算任务中,实验 2中手指表征方式存在 S-R 的相容性,如刺激“2+5”,效应则用“2根手指+5根手指”来表征,这也可能促进了个体反应的执行。
本研究也存在一些局限:首先,实验任务对于被试群体而言可能过于简单,并且十以内的加法运算仅是数学领域中非常微小的一点,未来研究可以探讨两位数、甚至多位数的数字加工任务(Reinert,Huber,Nuerk,&Moeller,2015;Meyerhoff,Moeller,Debus,&Nuerk,2012;Macizo &Herrera,2011),以期进一步拓展研究的深度。其次,实验3中的数字表征方式虽然在被试群体中得到了基本证实,但是被试对其的熟悉程度并没有得到严格的控制,这也可能是影响实验结果的一个因素,未来研究可对此进行严格的控制,探讨个体对效应的熟悉度对反应的影响。再次,在分析单个被试的数据时发现少数被试在不相容条件下的反应优于相容条件下的反应,这一结果与总体的表现相反,存在一种类似于效应反转的现象。许多研究认为,R-E相容性是S-R相容性的一个变式,或者说二者存在相似性(Chen&Proctor,2013;Theeuwes et al.,2015)。在 S-R 相容性以及Simon效应中存在效应反转,那么R-E相容性是否也会产生反转呢?最后,R-E相容性不仅可以从人生经验中建立联系,而且可以从近期获得的任意的S-R之间的关系中获得,Theeuwes等(2015)采用 Liefooghe,De Wenke,&Houwer (2013),Liefooghe,Wenke和De Houwer (2012)研究的变式直接考察了基于指令的R-E相容性现象,结果支持了 R-E相容性效应在概念层面上通过短时联结也可获得。那么当基于短时训练所形成的联结与基于人生经验所形成的联结产生冲突时,结果会如何?以及这种冲突所制造成的反转是否会影响到实验结束后的长时记忆?这些都是未来研究可以探讨的。
6 结论
不同的数字表征系统中均存在 R-E相容性效应,表现为相容关系时的促进和不相容关系时的干扰效应,支持了观念运动理论;相比客体材料,手指数字表征在相容条件下具有明显的匹配优势,支持了具身数量的观点。
Andres,M.,Michaux,N.,&Pesenti,M.(2012).Common substrate for mental arithmetic and finger representation in the parietal cortex.NeuroImage,62
(3),1520−1528.Ansorge,U.(2002).Spatial intention-response compatibility.Acta Psychologica,109
(3),285−299.Badets,A.,Pesenti,M.,&Olivier,E.(2010).Response-effect compatibility of finger-numeral configurations in arithmetical context.Quarterly Journal of Experimental Psychology,63
(1),16−22.Bender,A.,&Beller,S.(2011).Fingers as a tool for counting-naturally fixed or culturally flexible?.Frontiers in Psychology,2
,256.Bloechle,J.,Huber,S.,&Moeller,K.(2015).In touch with numbers:Embodied and situated effects in number magnitude comparison.Journal of Cognitive Psychology,27
(4),478−489.Bonny,J.W.,&Lourenco,S.F.(2013).The approximate number system and its relation to early math achievement:Evidence from the preschool years.Journal of Experimental Child Psychology,114
(3),375−388.Chen,J.,&Proctor,R.W.(2013).Response-effect compatibility defines the natural scrolling direction.Human Factors the Journal of the Human Factors &Ergonomics Society,55
(6),1112−1129.Chen,J.,&Proctor,R.W.(2015).Influence of response-effect feedback on learning and performance of a complex keypressing task:Morin and grant (1955)revisited.American Journal of Psychology,128
(2),197−208.Di Luca,S.,Lefèvre,N.,&Pesenti,M.(2010).Place and summation coding for canonical and non-canonical finger numeral representations.Cognition,117
(1),95−100.Di Luca,S.,&Pesenti,M.(2011).Finger numeral representations:More than just another symbolic code.Frontiers in Psychology,2
,272.Domahs,F.,Moeller,K.,Huber,S.,Willmes,K.,&Nuerk,H.C.(2010).Embodied numerosity:Implicit hand-based representations influence symbolic number processing across cultures.Cognition,116
,251−266.Fischer,M.H.,Kaufmann,L.,&Domahs,F.(2012).Finger counting and numerical cognition.Frontiers in Psychology,3
,108.Gaschler,R.,&Nattkemper,D.(2012).Instructed task demands and utilization of action effect anticipation.Frontiers in Psychology,3
,578.Hommel,B.,Alonso,D.,&Fuentes,L.(2003).Acquisition and generalization of action effects.Visual Cognition,10
,965−986.Hu,Y.R.,Zhang,L.,&Chen,M.(2014).Finger gnosis,movements and numeral representations contribute to numerical cognition.Psychological Development and Education,30
(3),329−336.[胡艳蓉,张丽,陈敏.(2014).手指的感知、运动以及数量表征对数字认知的促进作用.心理发展与教育,30
(3),329−336.]Hubbard,J.,Gazzaley,A.,&Morsella,E.(2011).Traditional response interference effects from anticipated action outcomes:A response-effect compatibility paradigm.Acta Psychologica,138
(1),106−110.Imbo,I.,Vandierendonck,A.,&Fias,W.(2011).Passive hand movements disrupt adults' counting strategies.Cognition,2
,201.James,W.(Ed).(1890).The principles of psychology
.New York:Holt.Janczyk,M.,Pfister,R.,&Kunde,W.(2012).On the persistence of tool-based compatibility effects.Zeitschrift Für Psychologie,220
(1),16−22.Klein,E.,Moeller,K.,Willmes,K.,Nuerk,H.C.,&Domahs,F.(2011).The influence of implicit hand-based representations on mental arithmetic.Frontiers in Psychology,2
,197.Koch,I.,&Kunde,W.(2002).Verbal response—effect compatibility.Memory &Cognition,30
(8),1297−1303.Krinzinger,H.,Koten,J.W.,Horoufchin,H.,Kohn,N.,Arndt,D.,Sahr,K.,… Willmes,K.(2011).The role of finger representations and saccades for number processing:An fMRI study in children.Frontiers in Psychology,2
,373.Kunde,W.(2001).Response-effect compatibility in manual choice reaction tasks.Journal of Experimental Psychology:Human Perception&Performance,27
,387−394.Kunde,W.(2003).Temporal response-effect compatibility.Psychological Research,67
,153−159.Liefooghe,B.,De Houwer,J.,&Wenke,D.(2013).Instruction-based response activation depends on task preparation.Psychonomic Bulletin &Review,20
,481−487.Liefooghe,B.,Wenke,D.,&De Houwer,J.(2012).Instructionbased task-rule congruency effects.Journal of Experimental Psychology Learning Memory &Cognition,38
(5),1325−1335.Macizo,P.,&Herrera,A.(2011).Cognitive control in number processing:Evidence from the unit-decade compatibility effect.Acta Psychologica,136
(1),112−118.Meyerhoff,H.S.,Moeller,K.,Debus,K.,&Nuerk,H.C.(2012).Multi-digit number processing beyond the two-digit number range:A combination of sequential and parallel processes.Acta Psychologica,140
(1),81−90.Niu,Y.B.,Shi,R.R.,&Cao,X.C.(2016).Preschool children’s approximate number system acuity and symbolic number abilities.Psychological Development and Education,32
(2),129−138.[牛玉柏,时冉冉,曹贤才.(2016).学前儿童近似数量系统敏锐度与符号数学能力的关系.心理发展与教育,32
(2),129−138.]Pfister,R.,&Kunde,W.(2013).Dissecting the response in response-effect compatibility.Experimental Brain Research,224
(4),647−55.Pfister,R.,Dolk,T.,Prinz,W.,&Kunde,W.(2014).Joint response-effect compatibility.Psychonomic Bulletin &
Review,21
(3),817−822.Reinert,R.M.,Huber,S.,Nuerk,H.C.,&Moeller,K.(2015).Strategies in unbounded number line estimation? Evidence from eye-tracking.Cognitive Processing,16
(S1),359−363.Sun,Y.,Chen,W.,&Ding,J.(2011).Ideomotor theory:The connotation and evidences.Advances in Psychological Science,19
(8),1138−1146.[孙月,陈巍,丁峻.(2011).观念运动理论:内涵与证据.心理科学进展,19
(8),1138−1146.]Theeuwes,M.,de Houwer,J.,Eder,A.,&Liefooghe,B.(2015).Congruency effects on the basis of instructed response-effect contingencies.Acta Psychologica,158
,43−50.Yang,Z.Y.,&Zhou,X.(2015).A review of researches on approximate number representation in early childhood.Studies in Early Childhood Education,
(11),44−55.[杨志艳,周欣.(2015).儿童早期近似数量表征的发展与特点.学前教育研究,
(11),44−55.]Yun,K.S.,&Proctor,R.W.(2012).Testing boundary conditions of the ideomotor hypothesis using a delayed response task.Acta Psychologica,141
(3),360−372.
