基于KHC算法的风力发电机组偏航控制系统

刘超+王世荣

摘要：针对现有的风力发电机组对风精度低、自然风速复杂，本文提出了一种将爬山算法与优化卡尔曼滤波相结合的算法，可以有效提高对风精度，该算法通过功率检测来提高对风精度，通过卡尔曼滤波算法来对未来时刻的风向量进行精确预测，避免偏航机构疲的劳动作和外界干扰。

【关键词】爬山算法 卡尔曼滤波 偏航控制

1 引言

本文提出了一种将爬山算法与优化卡尔曼滤波算法相结合的算法用于风机的偏航控制系统，通过检测风机输出功率并进行前后对比从而提高对风精度，同时采用优化卡尔曼滤波算法对风向量进行精准预测，有效减少风机疲劳动作。

2 偏航控制系统

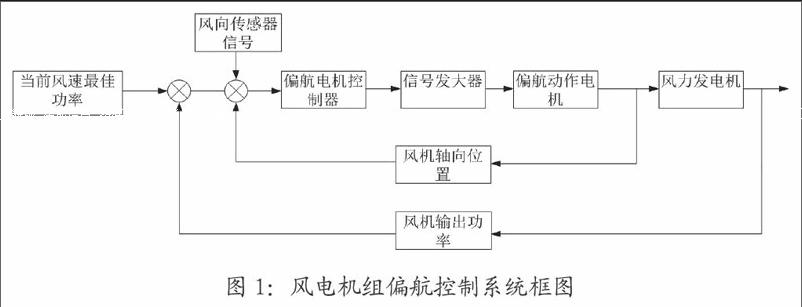
风力发电机组的偏航系统由风向标、偏航电机、偏航齿轮变速箱、机舵大齿轮等部分组成。通过风向标传感器采集风向信号，将风向信号传送至控制系统，控制系统根据风向信号发出控制命令，控制偏航电机开始转动，偏航电机转动带动机舵大齿轮旋转，从而控制风力发电机组的机身旋转进行准确对风。由于风向量具有随机属性为了使风力机组具有良好控制效果，本文中将采用双闭环控制系统，如图1所示：风机偏航控制系统外环采用风速输出功率环，跟踪风电机组的实时输出功率，将输出功率与监测的风速所对应的最佳输出功率相比较，判定风机工作状态。风机内环采用的是风向环，通过采集、监测风向信号并与风机机舵偏向位置进行比较，当风机未处于最佳工作风向时，控制系统发出控制信号，控制偏航电机运转，从而调整风机对风角度，使风机达到最佳风向位置。风电机组偏航控制系统框图如图1所示。

3 爬山一优化卡尔曼滤波算法（KHC算法）在风电机组中的应用

3.1 爬山算法

风电机组系统实时跟踪风力发电机的输出功率，然后采用递归调用的方法，将输出功率P₁分别与P₂、P₃、P₄、P₅、、、P_n相比较，当P₁2时则选择P₂为最大输出功率，然后再用P₂与后而的功率值做比较，取出最大的再次与后而的功率值比较，依次的进行下去，逐步提高输出功率，当P_n>P_max时将P_n赋值给P_max，从而选出最大输出功率，使风电机组的输出功率P_max无限接近当前风速的最佳输出功率P_best。

为了保证风机不频繁摆动，疲劳工作，在功率比较中应当设置系统对风误差精度P_s，当大于系统设定误差|P_max-P_best|>P_s时，偏航电机启动，按照预设方向偏转角度θ，直至IPmax.|P_max-P_best|s时，说明风机处于最佳工作状态，既能保证输出功率的最优化，又能避免小角度疲劳调整。

在风机偏航系统动作调整时，为了保证风机偏航方向正确，要实时监测输出功率，将此刻输出功率与前一时刻输出功率做比较，如P₂大于P₁证明偏航方向正确，若P₂小于P₁证明偏转方向不正确，则反方向偏转，依次进行比较P₂、P₃、P、P₅、、、P_n，由于风速属于实时变化的量，通过采样计算，最佳功率也是处于实时变化之中，因此我们需要对最佳功率进行实时调整。

3.2 优化卡尔曼滤波算法

优化卡尔曼滤波算法是根据上一时刻系统本身的数据计算出下一刻所需数据的预测值，然后再利用对应的传感器获取所需数据实际的测量值，将系统本身计算出的预测值与实际的测量值相结合算出最终的最优估计值，求出最终的最优估计值以后与系统计算出的预测值做比较，衡量最终的最优估计值数据值是否“靠谱”，如果偏差范围较小，说明最终最优估计值准确，在进行下次计算的时候则相应的增加预测值的比重，反之则减小预测值的比重。

優化卡尔曼滤波具体算法如下：

我们假设利用一个线性随机微分方程来表示风机偏航控制系统，

X（k）=AX（k-l）+BU（K）+W（k）

（1）

式中X（k）为K时刻系统对风向的计算估计值，X（k-l）为上一时刻风向的状态值，U（K）为系统的控制状态量、W（k）为系统噪声A、B分别为系统的参数可以根据实际系统确定其数值。

有了系统的计算估计值以后我们需要对计算估计值进行检验，看其是否“靠谱”，计算过程如下：

P（k|k_l）=AP（k|k-l）A^T+Q

（2）

P（k|k-l）是X（k）对应的COV，P（k-l|k-l）是X（k-l）对应的Cov，A^T表示A的转置矩阵，Q是系统过程的COV。经过以上两式计算以后我们便完成了系统对下一时刻状态变量的计算估计，接下来便开始求出最终的最优估计值，公式如下：

X（k|k）=X（k|k-l）+Kg （Z（k）-HX（klk-l））

（3）

（3）式中X（klk）为最新K时刻的状态最优估计值，X（klk-l）为上一时刻的系统计算预测值，Kg为卡尔曼增益、Z（k）为风向传感器的实际测量值，H为观测系数，将以上参数带入（3）中便可以计算出K时刻的最优估计值。

其中Kg为卡尔曼增益，在每一次计算中部需要用到它，通过卡尔曼增益来使估计值更加准确，计算公式如下：

Kg=P（k|k-l）H¹，（HP（k|k-l）H¹+R）

（4）

综合以上步骤我们就可以完整的求出一次最优估计值，但为了使系统不断的迭代下去，从而使最优估计值极限的逼近准确值，我们还需要不断更新X（k）状态量的COV，公式如下：

P（k|k）=（l-Kg（k）H）.P（k|k-l）

（5）

从而保证系统可以循环的计算下去，完成最终的最优估计。

通过以上五个公式的运用计算便可以得出系统的最优风向状态估计值，从而有效提高系统风能利用率，避免系统疲劳运转，有效提升系统工作效率。

4 总结

与传统风机相比，基于爬山一优化卡尔曼滤波算法的风电机组具有如下优点：

（1）通过此控制算法，可以有效的提高对风精度，提升风能利用率，减小了自然环境以及周围因素对风机的干扰。

（2）在保证了对风精度的前提下，通过加入的风向预测功能，有效的增强了对风动作，避免了风电机组的小范围疲劳动作。

（3）通过实验验证分析，有效的证明了KHC算法的有效性与可行性，但其中还有许多不足需要加以改进。

参考文献

[1]顾露香，乐秀璠，杨虞琨，李栅栅.KHC算法在风力发电机组偏航系统的运用[J].华电技术，2011，09： 92-94+98.

[2]《华电技术>第33卷总目次[J].华电技术，2011 （12）： 85-87.

[3]沈小军，杜万里.大型风力发电机偏航系统控制策略研究现状及展望[J].电工技术学报，2015 （10）：196-203.

[4]张慧宁，孙培德，张中炜，基于优化卡尔曼滤波的风电偏航控制器研究[J].控制系统，2010，26（01）：42-43.