基于NSGA—II算法的航母编队反潜火力优化
陈龙+马亚平

摘要:航母编队以其强大的战斗力被公认为海军装备中作战能力最强的武器,然而随着隐身潜艇作战能力的迅速发展和提高,航母编队面临的潜艇威胁不断加大,使得航母编队反潜作战越来越重要,探析航母编队反潜作战中火力分配优化迫在眉睫。本文首次将NSGA-II (Non-dominated SortingGenetic Algorithm-II)算法应用到航母编队反潜作战火力优化问题求解中。首先建立航母编队反潜作战模型;然后使用NSGA-Ⅱ算法进行求解;最后通过仿真实验得出航母编队反潜作战火力优化使用方案,论证了该算法和模型的可行性和有效性。
【关键词】NSGA-Ⅱ算法 火力优化 航母编队
集中优势兵力,以多击少,这是战争中一条基本作战原则。伟大的军事家毛泽东说过“集中优势兵力,各个歼灭敌人。”潜艇作为航母编队的“杀手”,使得研究航母编队反潜作战迫在眉睫。航母编队拥有多种水下警戒兵力,如何充分发挥各种水下警戒、反潜兵力的综合优势,如何精确使用火力,形成编队整体协同水下警戒、打击力量,以最小代价夺取最大作战效果是一项具有重要研究意义的课题。
火力分配是作战行动的重要组成部分,是作战决策的重要环节,国内外针对火力分配问题的研究非常广泛,而且根据不同的火力和目标提出相应的优化算法。很多算法已经被运用于火力分配优化中,大致可以分为常规解析火力分配法、智能进化火力分配法、混合式火力分配法三种方法。但未有对航母编队反潜火力分配进行优化,为解决提高航母编队作战仿真中火力分配的精度性、速度性,实现火力分配智能化,為编队指挥员提供可靠地辅助决策,本文首次将基于非支配排序遗传算法NSGA-Ⅱ(Non-dominated Sorting Genetic Algorithm -Ⅱ)应用到航母编队反潜作战火力优化问题求解中,对构建的航母编队反潜作战模型进行火力优化,从而取得较好的结果。
1 NSGA-I I算法的基本思想
NSGA-II算法进化操作流程:
输入:
(1)多目标问题MOP;
(2)终止条件;
(3)最优个体系数;
(4)种群规模、最大进化代数;
(5)适应度函数偏差。
输出:目标函数值、目标解。
步骤1初始化种群、个体的rank值。
步骤2.对种群根据非支配层级进行排序,形成非支配集;
(1)选择:二进制锦标赛法选择,将非支配集放入父代中,通过排挤和精英保留策略选出N个个体;
(2)交叉:进行交叉操作;
(3)变异:进行变异操作,产生新一代种群;
(4)更新目标函数值;
(5)更新领域中的解。
步骤3终止条件:如果函数评价次数大于等于Gen,停止计算并输出,否则返回步骤2,如图1所示。
2 模型建立
本文所用航母编队是借鉴美军和俄军航母编队兵力编成的情况,假设航母编队兵力编成的情况下展开研究。一般航母编队兵力编成有l艘航母、2-3艘导弹驱护舰、2-3艘导弹驱逐舰、1-2艘潜艇、1-2艘综合支援舰组成的共计7-11艘舰艇的航母编队。
2.1 模型假设
取典型航母编队由9艘舰艇组成,其中1艘航母、3艘导弹驱护舰、3艘导弹驱逐舰、1艘潜艇、1艘综合支援舰。在反潜作战中,潜艇很难与其他舰艇进行配合反潜,一般是单独进行行动才能发挥最大战斗力与隐身性特点,在火力分配中潜艇不参与其中。航母编队的攻潜武器包括航空深弹、航空鱼雷、火箭深弹、管装鱼雷、水声对抗系统五种武器,航母编队的五种攻潜武器可以进行组合生成多种攻击方案。对涉及到的作战背景作如下必要的假设:
(1)针对航母编队面临多个敌目标威胁的战术态势,假设编队防空作战不影响其对敌目标的攻击,每次攻击均为独立的随机事件;
(2)交战海区海情正常;编队各舰均装备水声对抗系统、舰载火箭深弹与舰载直升机(载航空深弹、鱼雷),编队对敌目标攻击武器能正确适时发射,且可用性与可靠性均为1;
(3)虽然水声对抗系统通过诱骗、干扰敌方鱼雷从而达到对敌目标防御的目的,在这里也理解为广义意义上的编队对敌目标攻击的火力之一;
(4)编队对敌目标预警距离足够大,各类武器系统均能组织有效的对抗;忽略编队各型武器实施攻击时之间的电磁等干扰。
2.2 反潜作战模型
航母编队是以编队形式遂行作战任务。通常情况下,编队编成中应包含不同战术技术性能特点的舰艇,先作如下变量定义:
3 NSGA-II算法操作
3.1 编码方式
本文采用十进制编码,一种编码方式对应群体中的一个个体,由于有Vxs个火力单位对m个敌目标进行攻击,因此染色体的长度为L=sxV×m(s为航母编队舰艇的数量,V为航母编队各舰艇拥有的攻击武器类型数量,m为敌目标的数量)。染色体基因xsvt表示航母编队舰艇s使用v型武器攻击敌目标t的火力分配的数量,如假设航母编队舰艇7艘,有5种攻击武器,对3个敌目标进行攻击的染色体。
3.2 适应度函数
依据毁伤目标期望最大原则,火力分配目标函数为:采用最小弹药消耗量、最大毁伤效益、航母编队最大生存概率,最大毁伤效益与弹药消耗量是相互矛盾的2个目标函数。使用这两个函数作为适应度函数式4-5:
4 仿真实验与结果分析
本文使用MatLab进行仿真实验,最优个体系数为0.3,适应度函数偏差为le-100。
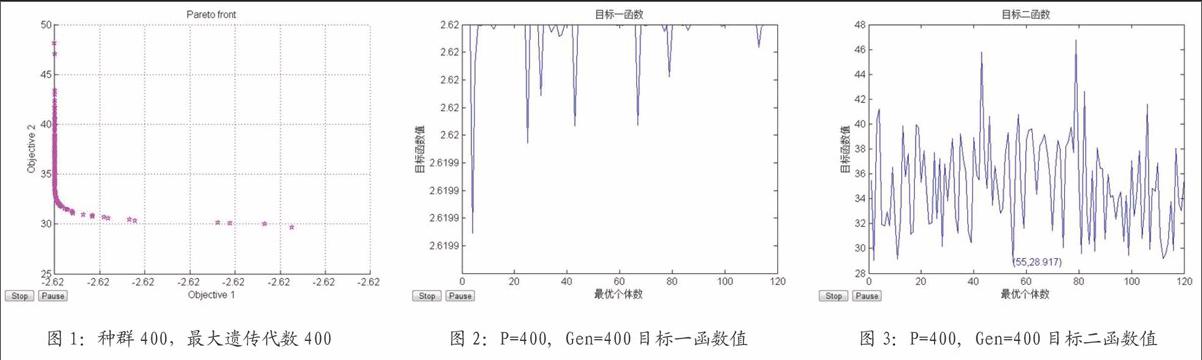
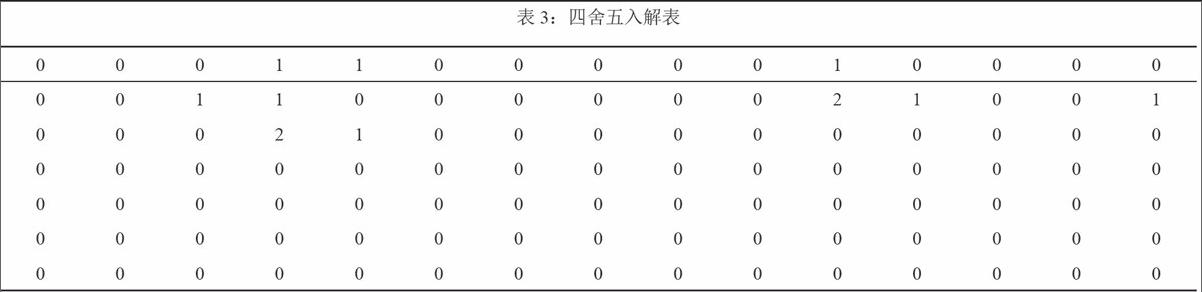
从图1至3可以看出,收敛速度和目标解的精度依赖于算法参数的选择,最大遗传代数影响进化算法收敛的速度,选用种群规模为400,最大遗传代数400代,得到航母编队火力优化结果如表1至表3所示。endprint
从表1至表3可以看出,向上取整解与四舍五入解对应的目标一函数值相近,但是目标二函数值相差较大,在不影响反潜作战效果的前提下,可以取四舍五人解,从而取得整体的性价比较高、消耗的弹药量较少。需要注意的是当航母编队使用航空深弹、航空鱼雷攻击时,是利用舰载直升机携带相应弹药完成攻击,下而不敷述,从仿真实验结果可以得出航母编队反潜火力优化结果:
航母编队中1号航母使用管装鱼雷1枚攻击目标1,使用航空深弹1枚攻击目标3,对目标1-3使用水声对抗系统;2号驱逐舰使用火箭深弹1枚、管装鱼雷1枚攻击目标1、使用航空深弹2枚、航空鱼雷1枚攻击目标3,对目标3使用水声对抗系统;3号驱逐舰使用管装鱼雷2枚攻击目标1,对目标1使用水声对抗系统;4号至7号舰艇根据态势变化,实时跟踪监视目标听令行动,弹药最小消耗量为12枚。
通过仿真实验验证了NSGA-H算法和反潜作战模型的有效性,得到的航母编队反潜作战火力分配方案,能够为航母编队指挥员提供一定的作战辅助决策。
參考文献
[l]Matlin S.A Review of the Literature on the Missile-Allocation Problem[M].INFORMS.1970.
[2] Lloyd S P,Witsenhausen H S.Weapons allocation is NP-complete [C]. IEEE Summer Conference on Simulation.1986.
[3]谭乐祖,张峥,孙仲元,多型反舰导弹混合攻击异型舰艇编队多目标整数规划火力分配模型[J].兵工自动化,2016,35 (08):47-49.
[4]L.M.Gambardella,E.Taillard, and G. Agazzi.MACS-VRPTW:A multiple ant colony sys tem for vehicle routing problems with time windows. In D.Comne,M. Dorigo,F. Glover,D. Dasgupta, P.Moscato,R.Poli,and K.V. Price, editors, New ldeas in Opt imization, McGraw-Hill, 1999, pp.63-76.
[5]隋永华,郭雷,俞利新,王海晏,改进的微分进化算法求解空战火力分配问题[J].火力与指挥控制,2012,37(12):118-121.
[6]董朝阳,路遥,王青,改进的遗传算法求解火力分配优化问题[J].兵工学报,2016, 37(01): 97-102.
[7]马宏斌,王玉生.基于改进型遗传和蚁群混合算法的防空兵群火力分配模型[J]. 武器装备自动化,2007.26(07): 3-4.
[8]罗佳,薛青,王之腾,张宏军,作战仿真中火力分配优化算法研究[J].计算机仿真,2013, 30 (10): 62-66.
[9]周兴旺,从福仲,庞世春,侯满义,辛腾达,基于贝叶斯混合博弈的空袭火力资源分配决策模型[J].火力与指挥控制,2016,41(07):18-22.
[10] Deb K,Agrawal S,Pratap A,et al.A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi- objective Optimization: NSGA-II [C]// International Conference on Parallel Problem Solving From Nature. Springer-Verlag, 2000: 849-858.endprint

