连续波雷达强脉冲干扰剔除的算法
宋文佳

摘要:本文分析了强干扰对连续波雷达的影响,提出了强干扰剔除的算法,从而消除了强干扰对连续波雷达目標检测的影响,改善了雷达的检测性能。并通过仿真验证了强干扰剔除算法的性能,在FPGA中实现了该算法。
【关键词】连续波雷达 消除强干扰 FPGA算法
1 引言
线性调频连续波雷达具有高距离分辨率、低发射功率、高接收灵敏度、结构简单等优点,不存在距离盲区,具有比脉冲雷达更好的反隐身、抗背景杂波和抗干扰能力和特别适用于近距离应用的特点。但是强脉冲干扰会污染回波信号的频谱,将目标信息掩埋在强脉冲干扰的频谱中,不利于目标的检测。
强脉冲对回波信号的频谱产生较大影响,目标的频谱掩埋在脉冲频谱中,致使出现假目标或是将真目标掩盖,不利于真目标的检测。弱脉冲干扰情况下,脉冲的频谱对回波信号的频谱影响较小,其幅度信息比较小,对后而的目标检测不会产生影响。
2 强干扰剔除算法
2.1 分块剔除和平均算法
强干扰剔除采用剔除和平均算法,当有较强的1个或是多个强脉冲干扰进入时,只会引起排序结果的变化,对门限的影响较小,该算法既能保证在无强干扰情况下不剔除目标信息,又能确保在强干扰情况下获取较为接近目标信息的门限,较好的剔除强干扰。
强干扰检测方法采用峰值检测,若检测值大于门限,则置零处理;否则,保持原值。
2.2 滑窗剔除算法
该算法与剔除和平均算法的不同点在于检测门限的计算。剔除和平均算法门限的计算与整个调频周期内的回波数据有关,而滑窗剔除算法的门限计算仅与窗内的回波数据有关。
滑窗算法的门限计算流程如下:
(1)将一个周期内的回波采样数据取模。
(2)将上一周期回波数据的取模后均值乘以系数A,作为固定门限。
(3)将一个调频周期的1024个回波数据固定门限比较。若小于门限将数据置为该值,若大于门限则保留原值。将其作为滑窗的门限计算数据。
(4)滑窗方法计算:设置窗大小为N,取待检测单元前N个单元取模做平均,将该均值乘以系数3作为检测的门限。
(5)在下一检测单元门限计算时,将该单元设置为上一周期数据取模后的均值,进行门限的计算。
该门限计算时的难点在于:一是固定门限计算中A的选择;二是滑窗检测中乘积因子的计算。在峰值检测中,若检测单元大于门限,将该检测单元置零,否则保留原值。
3 算法MATLAB仿真分析
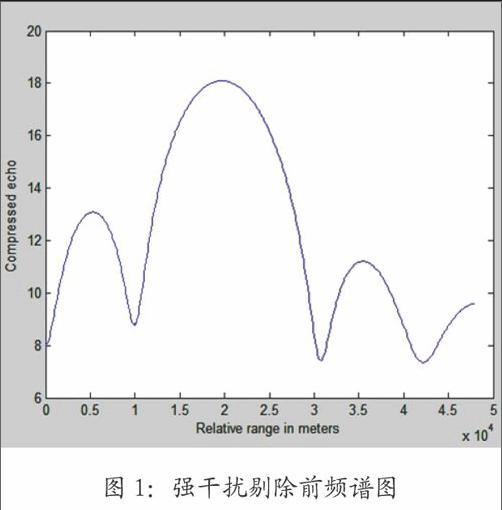
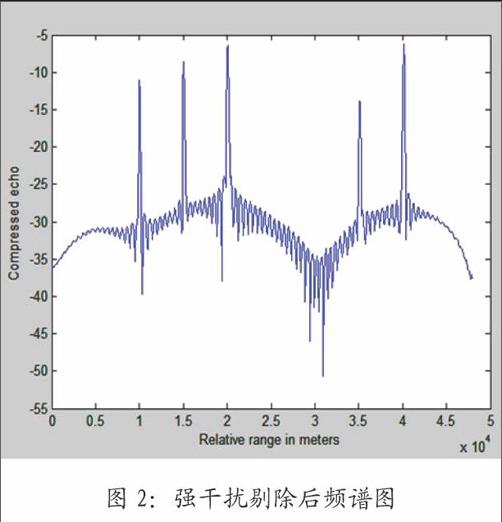
图1、图2为强脉冲干扰情况下,目标时域回波信号经过剔除和平均算法前后的频谱图,可以看出,经过剔除和平均算法后,强脉冲干扰被剔除。
4 FPGA实现
根据强干扰剔除的算法,在FPGA平台上实现,选用Stratix II系列的EP2S60F672C5芯片,资源利用情况如图3所示。
FPGA仿真结果显示,在无脉冲干扰的情况下,经过强干扰剔除后,有用的目标信息得以保留,该算法适用于无强脉冲干扰情况。在强脉冲干扰的情况下,脉冲干扰被剔除,有利于目标的检测。设计结果与MATLAB仿真完全一致,达到了预期的要求。
5 结论
强脉冲对连续波雷达的干扰,会污染雷达的频谱,不利于雷达的信号检测。本文提供了强干扰剔除的算法,并验证了算法的有效性。
参考文献
[1]杨建宇.线性调频连续波雷达理论与实现[D].成都:电子科技大学电工学院(电子科技大学博士论文),1991.
[2]周小燕.LFMCW雷达采集与处理研究[c].(电子科技大学硕士学位论文),2005.
[3]苗树立,LFMCW雷达信号处理方法及实现研究[D],成都:电子科技大学电子工学院.2004.
[4]王金明,杨吉斌,数字系统设计与VerilogHDL [M].北京:电子工业出版社.2002.endprint

