CT系统参数标定和图像重建
康宁 赵汗青 李霖龙
摘要:本文采用反向求解的方法,在旋转中心任选的情况下,利用几何法确定旋转中心、用特殊值法快速求解探测器的间距、利用穷尽算法求出探测器的方向。在标定参数后,利用滤波反投影重建算法进行重建图像。
关键词:CT系统;参数标定;成像原理;滤波反投影;窗口处理
中图分类号:O29 文献识别码:A 文章编号:1001-828X(2018)021-0360-03
引言
二维CT系统由发射器一探测器系统组成,发射器发射一组平行的x射线,经过一段固定的距离,被相应的模板吸收能量后,垂直地被等距排列的探测器接受。探测器上接受的值为经位置固定不动的二维待检测介质吸收衰减后的一个表征射线能量的值,再经过增益等处理后得到一个最终值。整个系统围绕旋转中心旋转180次,对每一个方向,512个探测器都会返回一个最终值,形成512个数据,再经过180次旋转,得到180组信息。
由于CT系统在安装时存在一些误差,可借助已知模板对系统进行参数标定,并根据参数标定结果对未知样品进行图像重建。本文主要研究了CT系统成像误差以及信号吸收率的问题,做出了cT系统参数标定和图像重建。
一、CT系统参数标定
1.探测器间距
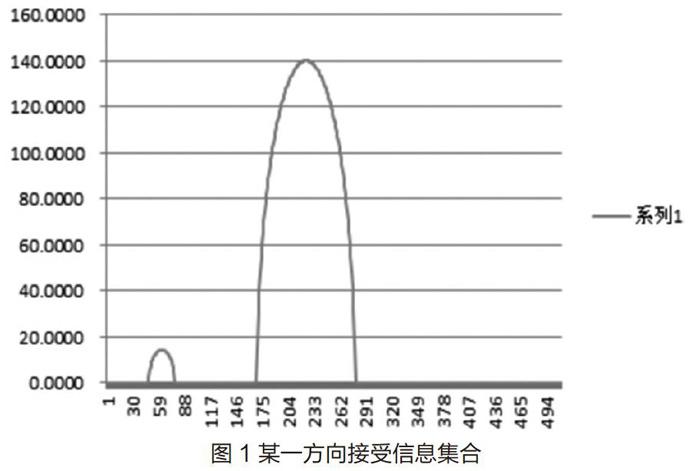
选取第一次旋转的数据,显然不为O的探测值是由于对应的x射线穿过了圆形介质或者椭圆形介质导致的。选取某一合适方向,利用Maflab,根据经过小圆的射线,我们可得出经过小圆的29个探测器的间隔距离,因为小圆的直径被这29个探测器所扫描,且其直径与x射线垂直,所以探测器元件的间隔为:
2.探测器旋转方向
通过对每一方向512个探测器所接受到的信息,绘出180幅根据接受信息所拟出的图像,为了进一步研究,利用线性回归、最小二乘法的办法,将本来经过圆的射线的接受信息,变成了按原路径发射但是不受圆介质的吸收效应的影响的接受信息,使得图像只保留x射线经过椭圆的对应接受信息的拟合图像。先建立一个合理的参考系,以椭圆的中心为原点,将穿过椭圆中心和小圆中心的直线定义为x轴,将穿过椭圆长轴的直线定义为y轴。
接受信息与相应路程d有如下关系。
J=1.7722×d(式1.1)
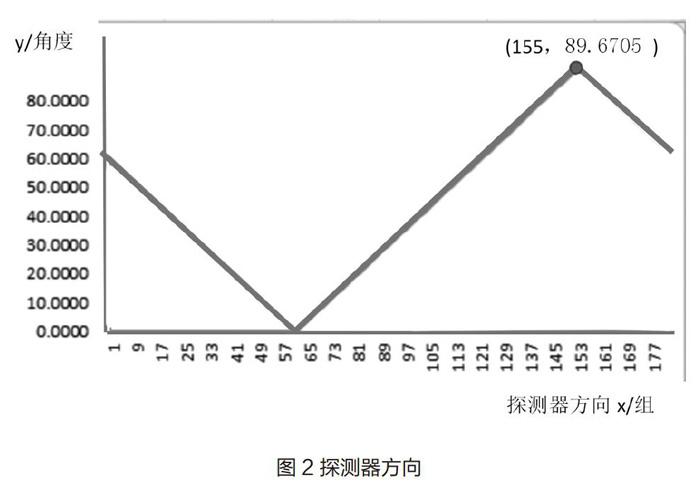
运用穷尽算法的思想,拟合出椭圆大量的中心半径与其相应的斜率之间的关系,并应用matlab绘图。通过对每个方向的曲线分析得到该方向上的极大值,求得相应的斜率,并用反三角函数即得到相应的角度,即方向。
3.探测器旋转中心
利用反雷登变换来实现图像的重建。在Matlab中运用irandon函数实现逆变换。程序运行之后得到了下图:
通过确定扫描图像对角线交点与椭圆中心的相对位置来确定原图中的旋转中心。首先画出图像对角线交点以及椭圆长轴与短轴的交点,然后通过测量与计算我们可以得出在变换以后图像中心相对于椭圆中心的相对位置,此相对位置变换到原图就是旋转中心。
在图中作出四条辅助线,其中红线为图像的对角线,黄点为对角线交点,蓝线为以椭圆的两个轴延伸的直线。其中通过辅助线我们可以得出黄点相对于蓝线交点的相对位置为(-10.3697,6.6461),所以旋转中心的位置为(-10.3697,6.6461)。
二、CT系统图像重建
CT成像的本质是衰减系数成像,通过对接收器各个方向的能量值进行滤波反投影成像,可以求出该介质各体素的衰减系数值,获得衰减系数的二维分布,即衰减系数矩阵。根据CT值的定义以及CT值与衰减系数的关系,将衰减系数矩阵转化为CT值矩阵,并利用MATLAB将各像素的CT值转化为灰度,生成CT影像。
1.求解衰减系数分布函数
根据滤波反投影重建算法推导出衰减系数分布函数的求解过程:
假设物体在xy平面内都不均匀,衰减系数f=f(x,y)为被测物体某断面的线性衰减系数的分布函数。当初始强度为I0的x射线穿过物体时,探测器检测到的I服从Beer定理:
gθ(l)为被检测物体某断面的衰减系数在θ方向的线积分值。
根据中心切片定理的定义,f(x,y)在某一方向上的投影函数gθ(l)的一维傅里叶变换函数Gθ(l)是f(x,y)的二维傅里叶变换函数F(ρ,θ)在(ρ,θ)平面上沿同一方向且过原点的直线上的值。
根据所求得的180个方向,可以得到对应的180个投影函数函数数据,通过傅里叶变换:
从旋转方向可知,180组板旋转角度基本是均匀的,则上式可以变形为:
理想的滤波器是无法实现的,我们需要对理想滤波函数进行加窗处理。为了使重建图像轮廓清楚,且尽可能减小振荡现象引起的图像模糊,采用S-L滤波函数,使用较平滑的窗函数:
2.将衰减系数矩阵转化为灰度值矩阵
CT值为通过衰减系数换算得到的每个体素对x线的吸收能力,其计算公式为:
根据式(2.13)可以实现衰减系数与CT值的互相转化。Matlab可以将求解出的CT值矩阵转化为灰度值矩阵并生成图像。
以下为求解过程:目的是消除不同介质体素衰减系数差异不同的量纲影响。吸收强度值为对灰度值矩阵进行归一化处理后映射到[0,1]之间的结果。采用了离差标准化方法,其转换函数如下:
根据灰度值矩阵G以及归一化处理过程,可以得到256×256的吸收强度矩陣。根据已经建立的坐标轴,以及椭圆模板几何信息与坐标轴的对应,定位出吸收强度在坐标轴中的位置,几何形状以及对应的吸收率。
三、结语
根据上述方法,可以通过已知模板信息对安装好的CT系统进行参数标定,并基于滤波反投影算法,利用Matlab软件,进行cT系统的图像重建。