一类二阶微分方程的振动准则

黎小贤，杨 菊，李全娣，戴丽娜

(广东石油化工学院 理学院数学系，广东 茂名 525000)

1 引 言

本文主要研究二阶半线性中立型[1]微分方程

(E)

其中

h(t)=x(t)+p(t)xτ(t)，α>0,r,σ∈C1[t0,∞),(0,∞),p,g,τ∈[t0,∞),R

0≤p(t)≤1,g(t)>0.若(E)有无穷多个零点，则它为振动的；否则称它为非振动的[2-10]. 对二阶非线性微分方程的研究[10-12],以及对二阶半线性中立型微分方程振动性建立了一系列准则并给出证明方法，但研究所得结果还不够完善，本文对文[1]的振动准则进行研究，进一步改进其结果，得到一个新的振动准则.

ρ，δ∈C1[t0,∞),(0,∞)

满足

(A)

和

(B)

则方程(E)振动.

受文[1]启发，建立新的准则，主要对(B)条件改进得到相对完善的结果，使得只要文[1]中的α>0，且α可取偶数而不仅仅限于α≥1的两个奇数商.

2 主要结果

定理2.1设π(t0)<∞，若存在函数ρ∈C

[t0,∞)，R

满足

(2.1)

且

(2.2)

其中

则方程(E)振动.

证明：设方程有一个非振动解x(t)，且

x(t)>0，x

σ(t)

>0，x

τ(t)

>0，t≥t1≥t0

由方程(E)可得

p(t)

′≤0

在[t1,t]上，

r(t)

′是非増函数，则h′(t)是不变号的，那么分两种情况展开讨论.

(i)假设h′(t)>0,t≥t2≥t1

因为τ(t)≤t，所以h(t)≥h(τ(t))，即有

x(t)=h(t)-p(t)x(τ(t))≥h(t)-p(t)h(τ(t))≥

h(t)-p(t)h(t)=(1-p(t))h(t)

(2-3)

即

去绝对值，则(E)变成

(2.4)

(2.3)代入(2.4)得，

r(t)(h′(t))α

令G1(t)=g(t)(1-p(σ(t)))α，即有

r(t)(h′(t))α

′≤-G1(t)

(2.5)

(2.6)

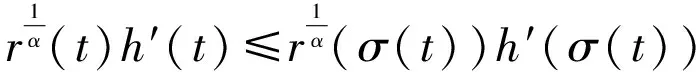
即

(2.7)

(2.5)两边对t求导，且由(2.6)和(2.7)得

(2.8)

即(2.8)式为

(2.9)

在[t2,t]上积分，即有

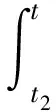
u(t2)-u(t)≤u(t2)

(2.10)

显然式(2.10)与条件(2.1)矛盾.

(ii)h′(t)≤0，同理可证得，因此，方程(E)振动

3 例 子

(3.1)

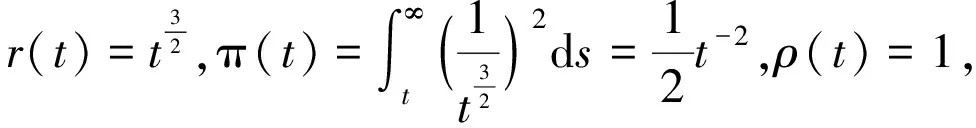
显然

G1(t)=g0

则有

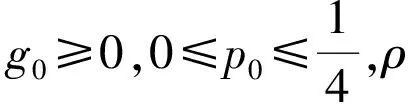
[1] Ravi P. Agarwal,Chenghui Zhang,Tongxing. Li Some remarks on oscillantion of second order neutral differential equations [J]. Appl. Math. Comput，2016，274：178-181.

[2] HAN Z，LI T,SUN S,SUN Y.Remarks on the paper[Appl.Math.Comput.207(2009)388-396] [J]. Appl. Math. Comput，2010，215：3998-4007.

[3] JIANG J,LI X . Qscillation of second order nonlinear neuteal differential equations [J]. Appl. Math.Comput,2003，135：531-540.

[4] LI T,YU W.Rogovechko,ZHANG C.Oscillation of second-order neutral differential equations[J]. Funke, Ekvacioj ，2013，56：111-120.

[5] YE L,XU Z. Oscillation criteria for second order quasilinear neutral delay differential equations [J]. Appl Math Comput， 2009，207：388-396.

[6] LI T,R P Agarwal,M Bohner. Some oscillation results for second-order differential equations [J]. J.Indian Math Soc，2012，79：97-106.

[7] B Baculíková,I Durina. Oscillation theorems for higher order neutral differential equations[J]. Appl Math Comput， 2012，219：3769-3778.

[8] M Hasanbulli,YU Rogovchenko. Oscillation criteria for second-order nonlinear neutral differential equations[J]. Appl Math Comput， 2010，215：4392-4399.

[9] ZHANG S,WANG Q.Oscillation of second-order nonlinear neutral dynamic equations on time scales[J],Appl Math Comput，2010，216：2837-2848.

[10] 林全文,庄容坤.二阶非线性椭圆型微分方程新的振动准则[J]. 中山大学，2013，52(2):57-61.

[11] 林全文,俞元洪.二阶非线性振动的Philos型积分平均[J]. 数学物理学报 ，2012，32A(4):661-339.

[12] 林全文,俞元洪.带有阻尼项的Emden-Fowler方程的区间振动准则[J]. 数学杂志, 2012，32 (4):316-722.