基于同质直方图和DS证据理论的彩色图像分割研究

陆小妍，周啸虎，张子齐

南京医科大学附属南京医院（南京市第一医院） 放射科，江苏 南京 210006

引言

彩色图像分割是图像处理的重要步骤，有利于目标识别与分析[1]。彩色图像通常是基于RGB颜色标准的，每个像素由RGB三基色编码组成。RGB三通道模式适用于彩色图像显示，但由于R、G、B三通道之间存在交叠，不利于彩色图像的分割与分析，数据融合技术可以克服此局限性。数据融合技术能充分考虑来自异种数据的差异性，进而获得最佳的目标组合。常用的数据融合技术有概率论、模糊逻辑理论、证据理论等[2]，其中Dempster-Shafer（DS）理论是一个强大灵活的数学工具，可处理不确定、不准确、不完整的信息。Mass函数，又叫概率分配函数，是DS证据理论发挥融合功能的最重要一步。

Mass函数没有固定形式，长期以来，众多学者在实际问题中构造Mass函数，以期发挥DS证据理论的最大优势[3]。在过去，学者研究模糊集与DS证据理论之间的关系，以此自动确定Mass函数；在近期，基于模糊C均值衍生出大量的模糊算法，均有很多局限性，比如抗噪声差、兼容性和隶属度与直观观念偏差很大。近几年，Gautier等[4]在研究从一组横断面重建各椎体的时候，采用活动轮廓模型完成图像初始分割，是一种基于信任理论的信息融合方法，但初始轮廓很难确定；Zimmermann等[5]根据经验研究得出一个基于目标点到原型成员之间距离的优良模型（Model for Membership Functions，MMFD），但受距离测度影响较大；Chaabane等[6]提出一个自动确定Mass函数的分割算法，基于模糊逻辑方法，每个图像像素分配一个与成员函数相匹配的Mass函数概率数，每个像素的成员隶属度由模糊C均值（Fuzzy C-Means，FCM）算法确定；Vannoorenberghe等[7]提出一种图像像素强度的信息论模型，其中Mass函数的预测主要基于高斯分布假设和直方图阈值（Model Mass Function Method Based on the Assumption of Gaussian Distribution，MMFAGD），但仅在包含两层的生物医学图像上进行测试。

本文提出一种基于同质直方图阈值和数据融合技术的彩色图像分割算法。同质直方图被用来表征图像像素的局部和全局信息，可检测三基色图像中所有的同质区域；采用高斯分布假设预测每个像素的Mass函数，然后使用DS合并规则完成最终的图像分割。

1 方法

由RGB三基色表征的彩色图像空间高度相关，图像像素强度改变，三通道的强度也相应改变，不利于图像分析与分割。在此背景下，DS证据理论被引入图像分割过程，在同质直方图的基础上，使用高斯分布假设产生合理的Mass函数，进而可采用DS证据理论可得最终的分割图像。

1.1 同质直方图分析

直方图阈值在单色图像分割中应用广泛，但存在仅能处理灰度水平图像、不能考虑到图像的空间分布信息等缺点。本文采用模糊同质直方图提取彩色图像中各基色图像的同质区域，能有效地克服传统直方图的局限性。

假设图像大小为M×N，gxy是图像在（x，y）位置像素pxy的强度,则以（x，y）为中心的d×d窗口的图像局部区域均值uxy和标准差vxy由公式(1)和公式(2)给出。其中x≥2，p＜M -1，y≥2，q≤N -1。

边缘是灰度图像局部像素pxy强度突变的部分，边缘强度可由边缘检测算子求得，由于本文不需要精确地提取边缘位置，综合计算量和实施的难易度，选用Sobel算子计算图像间断性和梯度大小作为边缘强度测度。Sobel算子如公式(3)所示[8]，其中Gx、Gy分别是x、y方向上的梯度大小。

因此，图像的同质性可由公式(4)表示，

窗口大小对图像同质性影响较大，窗口应尽可能较大，包含足够多像素的局部特征信息，且能提高平滑作用，降低梯度导数操作对噪声的敏感性，但同时掩盖了变化剧烈的局部信息，增加了计算量。经试验测试，计算标准差的窗口定为5×5，计算边缘强度的窗口为3×3。

通过公式(4)可确定同质直方图，然后采用阈值法分割各基色图像，阈值由直方图峰值点检测算法求得[9]。输入大小为M×N，灰度范围[0,255]的图像，假设图像同质直方图函数为h(i)，i∈[0,255]，每个像素点的同质性h(pi)∈[0,1]。步骤如下：

第一步：构建直方图局部最大值的集合P0；

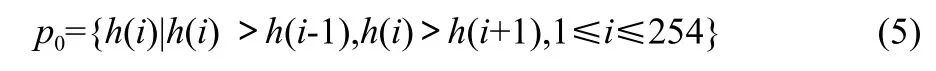
第二步：在集合p0中检测出显著峰值点p1；

第三步：分割阈值排除规则：

（1）对于任意峰值点，满足h(i)/h(imax)＜0.05时，即可排除；

（2）当两个峰值点相近取其一，即(p2-p1)≤12时，h=max[h(p1),h(p2)]；

（3）当两个峰值点之间波谷不明显时，去除一个峰值点。hav1是峰值点p1到p2的均值，hav2是峰值点p1和p2的均值。

1.2 基于DS证据理论的图像分割

分割的目的是将图像分成多块的同质区域，本文首先采用同质直方图分割各基色初始图像，然后采用DS证据理论融合三基色图像像素得到最终的彩色分割图像。DS证据理论是概率论的一种延伸，在解决多层信息决策分析、信息融合等问题上具有绝对优势。

DS证据理论主要涉及基本概率分布函数、信任函数、似然函数和合并规则等概念[10]。设D是变量Hi的集合，且D中所有元素是互斥的，则称D为Hi的样本空间，也称D为辨别框。D的任意一个子集A都对应于一个关于Hi的命题，称该命题为“Hi的值在A中”。

主要步骤如下：

（1）概率分配函数：在辨别框D上的基本概率分配函数是一个2D→[0,1]的函数M，称为Mass函数，且满足其中m(A)＞0的A称为焦元，m(A)称为A的基本概率数。

（2）信任函数：信任函数表示对命题Hn为真的可信度，由Bel(Hn)表示。

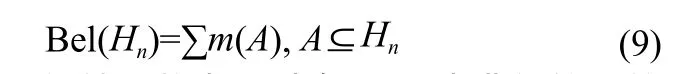
（3）似然函数：似然函数表示对命题Hn为非假的可信度，由PI(Hn)表示。

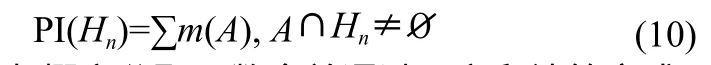
（4）合并规则：概率分配函数合并通过正交和计算完成。

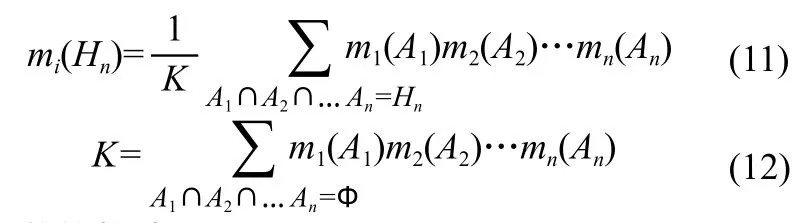
1.3 Ma s s函数的构造

单一假设Ci的Mass函数可由灰度水平gxy属于第i类的高斯分布函数所得，形式如公式(13)所示[11-12]。式中gq是像素pxy在三层信息源图像(x,y)位置上的强度(q=1,2,3),μi, σi2分别是各基色图像上第i类Ci的均值和方差。

实际上，在分配一个灰度水平gxy到具体类别时，经常遇到两个类别的Mass函数值相接近，造成模糊不清，此时需要采用二重单一假设的联合Mass函数准确分配类别，如公式 (15)所示[13-14]。其中 urs=(ur+us)/2, σrs=max(σr,σs)。同理可将Mass函数推广到m重单一假设。

一旦预测出三基色各层图像的Mass函数，正交和运算将被用来融合三基色各层图像，得到分割后的彩色图像。式中○+表示DS证据理论的正交和法则。

1.4 本文分割算法的流程

综合同质直方图、高斯分布假设和DS证据理论，可得本文提出的分割算法流程：第一步：输入彩色图像，计算图像同质特征和图像同质直方图；第二步：采用峰值点检测算法获取分割阈值，将各基色图像分成同质子区域；第三步：采用高斯分布假设估算各基色图像的Mass函数；第四步：计算各基色图像的Mass函数的正交和，完成三层图像的融合，获得最终的彩色分割图像。

2 结果与分析

选用12幅包含医学彩色图像和人工合成彩色图像进行仿真实验，均由RGB三基色组成，图像尺寸为256×256×3，所有的仿真实验均在MATLAB平台上实现。图像分割效果联合使用定性和定量分析进行评价，定性分析主要基于人眼目测的方法，参考标准为图像对比度、清晰度、亮度等指标。定量分析采用分割灵敏度评价，如公式(17)所示[15-17]。式中Nc表示正确分类的图像像素数目。

2.1 基于同质直方图的各层图像分割结果

选取一幅细胞的彩色医学图像，采用同质直方图阈值法对RGB各层图像进行分割，结果见图1。可以看出，各层的分割结果均不准确，在R（图1b）、G（图1c）、B（图1d）各层图像中分别含有4、3和2个细胞，R层分割图像识别出所有细胞，分割准确性优于G和B两层，但细胞中缺失了某些信息，这是由于一层图像缺乏足够的信息，且各层图像之间高度关联。因此，为了精确完整的分割图像，需要对3层图像进行融合操作。

图1 基于同质直方图的彩色图像分割

2.2 不同彩色图像分割算法效果比较

选取人工合成的RGB图像，包含两个类别，RGB各层图像灰度范围为[0,255]，传统方法MMFD，MMFADG和本文提出算法的定性、定量比较结果，见图2～3。

图2 不同分割算法效果比较

图3 12幅图像基于不同分割算法的灵敏度

图2显示了不同分割算法效果比较，可以看出，图2e中细胞被清晰完整地分割出来，而图2c和图2d图像细胞中有孔洞和明显的误分割点，表明基于本文算法的分割图像视觉效果更佳。

图3给出12幅图像基于不同分割算法的灵敏度比较结果，其中2号图像基于MMFD、MMGFAGD和本文算法的分割灵敏度分别为68.23%、79.66%和97.27%，可以看出即使在噪声环境下，本文所用算法的分割效果依然最佳，这是由于传统的直方图方法仅考虑图像的全局信息，本文的同质直方图综合了图像全局和局部信息。

2.3 基于不同Ma s s函数的分割效果比较

Mass函数是DS证据理论的关键，本文在人工合成图像和医学实例图像上比较不同Mass函数的分割效果，结果见图 4～6。

图4是对6层人工合成图像的分割比较，基于硬C均值（HCM）和FCM算法产生的Mass函数只能将源图像分割成4和5类同质区域，而基于本文算法能准确分割出6类同质区域。

图5是医学实例图像的分割结果，源图像包括3种色彩，基于HCM和FCM的分割算法不能分割出目标区域，且分割图像中仅包含两种色彩，但基于本文算法的分割图像中目标与背景清晰分离，保留了源图像中的3种色彩。表明本文分割算法的优越性。

图5 1号医学图像基于不同Mass函数分割结果比较

图6 12幅图像基于不同Mass函数分割算法的灵敏度

图6是12幅图像基于不同Mass函数分割算法的灵敏度比较结果，其中10号人工图像基于HCM、FCM和本文算法的分割灵敏度分别为64.42%、79.58%和96.97%；1号医学图像基于HCM、FCM和本文算法的分割灵敏度分别为86.74%、89.45%和94.23%。可知基于本文所用Mass函数的分割效果最佳，这是由于HCM和FCM算法仅考虑灰度水平上各像素的隶属度。

3 结论

本文提出一种新颖的基于同质直方图阈值法和数据融合技术的彩色图像分割算法。首先各基色图像被同质直方图阈值法分成多块均匀区域，然后D理论的合并规则融合三层初始图像，获得最终的彩色分割图像。实验结果表明，较其他传统分割算法和Mass函数预测方法而言，本文算法考虑到图像的局部和全局信息，可获得精确、强健的分割结果，是一种可行的、通用的彩色图像分割算法。

[1] Incetas MO,Demirci R,Yavuzcan HG.Automatic segmentation of color images with transitive closure[J].AEU-Int J Electron C,2014,68(3):260-269.

[2] Szczypiński P,Klepaczko A,Pazurek M,et al.Texture and color based image segmentation and pathology detection in capsule endoscopy videos[J].Comput Meth Prog Bio,2014,113(1):396-411.

[3] 韩建栋,朱婷婷,李月香,等.结合粗糙集与分层思想的彩色图像分割算法[J].计算机应用,2015,35(7):2020-2024.

[4] Gautier L,Taleb-Ahmed A,Rombaut M,et al.Aide à la décision de segmentation d’image par la théorie de Dempster-Shafer: application à une séquence d’images IRM[J].ITBMRBM,2001,22(6):378-392.

[5] Zimmermann HJ,Zysno P.Quantifying vagueness in decision models[J].Eur J Oper Res,1985,22(2):148-158.

[6] Chaabane SB,Sayadi M,Fnaiech F,et al.Dempster-Shafer evidence theory for image segmentation: Application in cells images[J].Int J Adapt Control,2009,5(2):728-734.

[7] Vannoorenberghe P,Colot O,Brucq D.Color image segmentation using Dempster-Shafer’s theory[J].IEEE,1999,4:300-304.

[8] Khan A,Ullah J,Jaffar MA,et al.Color image segmentation: a novel spatial fuzzy genetic algorithm[J].Signal, Image Video P,2014,8(7):1233-1243.

[9] 朱征宇,王丽敏.彩色图像分割的FCM初始化方法[J].计算机应用研究,2015,32(4):1257-1260.

[10] 王江涛,练煜,石红岩,等.结合模糊C均值聚类和边缘检测算法的彩色图像分割[J].兰州文理学院学报(自然科学版),2015,29(2):61-65.

[11] 葛亮,杨竣铎.基于蚁群优化多层图划分的彩色图像分割方法[J].计算机应用研究,2015,32(4):1265-1268.

[12] An NY,Pun CM.Color image segmentation using adaptive color quantization and multiresolution texture characterization[J].Signal, Image Video P,2014,8(5):943-954.

[13] Pal NR,Pal SK.A review on image segmentation techniques[J].Pattern Recog,2015,26(9):1277-1294.

[14] Kim S,Nowozin S,Kohli P,et al.Higher-order correlation clustering for image segmentation[J].IEEE T Pattern Anal,2015,36(36):1761-1774.

[15] Zheng Y,Byeungwoo J,Xu D,et al.Image segmentation by generalized hierarchical fuzzy C-means algorithm[J].J Intell Fuzzy Syst,2015,28(2):4024-4028.

[16] Smistad E,Falch TL,Bozorgi M,et al.Medical image segmentation on GPUs-A comprehensive review[J].Med Image Anal,2015,20(1):1-18.

[17] Torbati N,Ayatollahi A,Kermani A.An efɦcient neural network based method for medical image segmentation[J].Comput Biol Med,2014,44(C):76-87.