基于改进连通域标记的手绘草图符号分割

刘明明，方贵盛

(1.浙江大学 机械工程学院,浙江 杭州 310027；2.浙江水利水电学院 机械与汽车工程学院，浙江 杭州 310018)

近年来，随着智能手机、平板电脑等触屏设备的普及，人机交互的方式发生很大的改变，触控成为占据主流的输入方式.人们可以把头脑中想象的事物在触摸屏上手绘出来，形成手绘草图.手绘草图通过识别转化为规范的矢量图，对后续处理、修改与保存等具有重要意义.草图分割是手绘草图识别的重要环节，其好坏直接影响手绘草图识别的结果.与普通的图片相比，设计人员设计的草图一般没有颜色等信息，大多为二值图像，并且由于设计的随意性与笔划的不连贯导致草图单元不完整等问题，使得草图分割起来更加困难.因此，如何从一系列连续的笔划流中准确地分离出一些具有特定含义的符号，并加以识别，对提高手绘草图识别效率与质量具有重要作用.

图像分割是将图像分割成包含相似属性的不同区域.为了对图像分析和解释有意义，图像分割出的区域应与描述的对象或者感兴趣的特征密切相关.图像分割是将低层次的灰度或者彩色图像处理向高层次的图像描述的第一步，而分割的可靠性则依赖对图像的精确分析.分割的技术可分为上下文和非上下文的.上下文的图像分割技术利用分组在一起的像素具有相似的灰度级别或者空间位置来分割；而非上下文的分割技术则是不考虑像素之间的空间关系.属于上下文的图像分割算法有根据边缘或者连接状况来分割的图像算法[1-3]和根据区域相似度来进行分割的图像算法[4-6]等.这些算法都是依靠像素之间的空间关系来分割，在区域分明或者边界清晰的条件下能够有很好的分割效果.属于非上下文的分割算法比较常见的就是根据阈值来进行分割的算法[7-8]，还有根据特定理论进行图像分割的方法[9].

近年来，随着对图像分割精度的要求，以往那些基于区域或者边缘的分割方法并不能很精确的分割出目标区域.虽然也出现过一些试图提高分割精确度的算法[10-11]，但是都不能从根本上解决问题，所以基于像素的算法就有着在处理复杂图像独到的优势.传统的连通域标记算法在处理图像分割过程中运行速度较慢，扫描次数多，造成了算法效率低下.提高连通域标记算法性能可以采用减少图像的扫描次数，减少回溯扫描时间，一次扫描尽可能多地提取连通域等信息.基于此，本文提出了一种连通域标记的改进算法，通过减少扫描次数来缩短运行时间，提高算法的性能.由于本文针对的是对电气草图的分割，所以要先对草图进行一些处理，例如去除元器件之间的连接特征，边缘检测，膨胀等操作.

1 基于霍夫直线变换检测电气图中元器件的连接特征

1.1 霍夫直线检测技术

霍夫(Hough)变换在计算机视觉领域得到了广泛的应用，其主要应用于模式识别领域中对二值图像进行直线检测[12].霍夫变换主要用于计算特征的全局描述，也可以理解为对每个坐标点，计算其对全局一致性的贡献.霍夫直线变换则是将一组离散图像的点拟合成一条直线，其示意图(见图1).

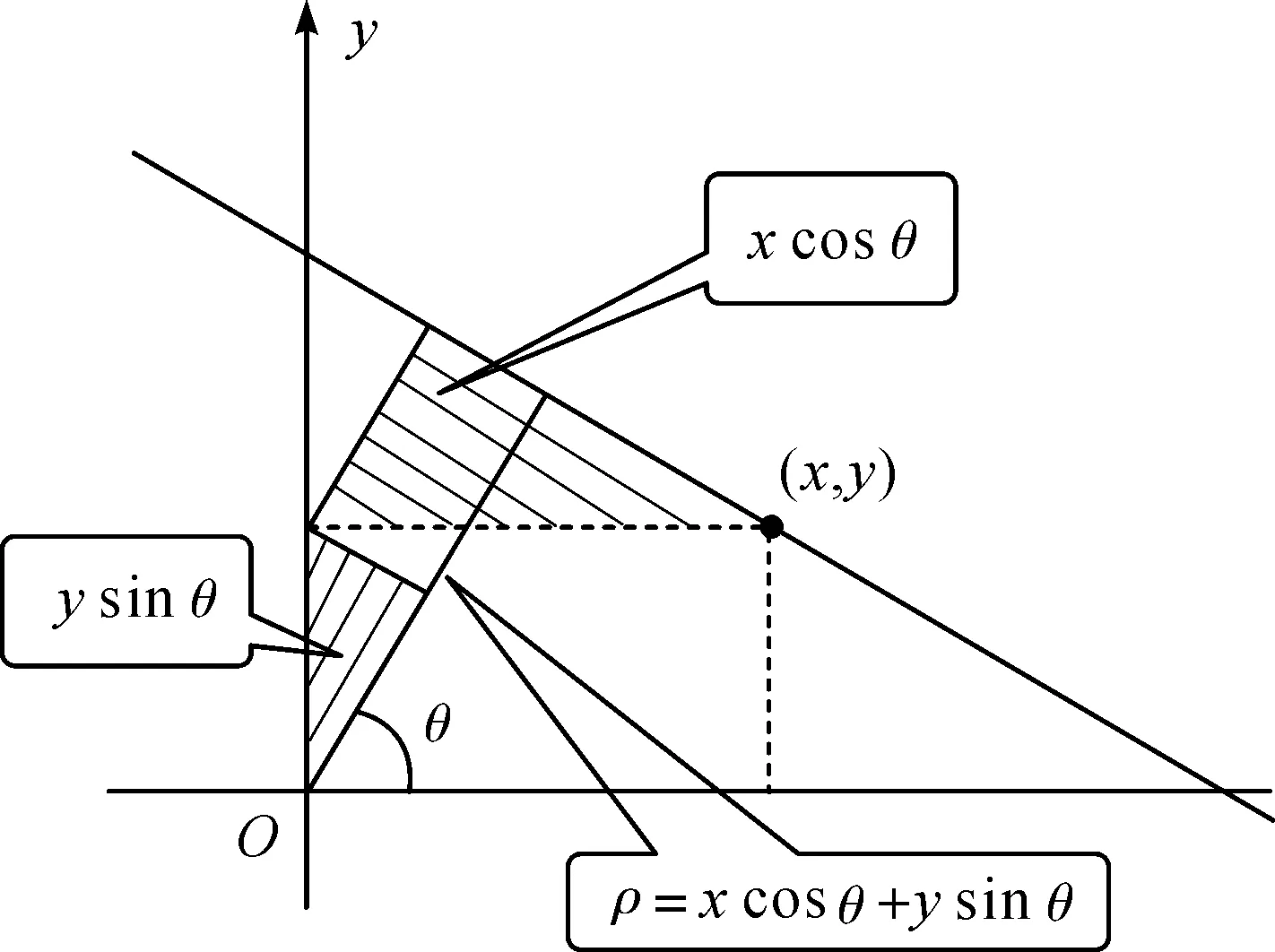
图1 霍夫直线变换示意图

平面直角坐标系内直线的表示形式为:

y=kx+b

(1)

其中，k为斜率，b为截距.

霍夫直线变换就是将原本在笛卡尔坐标系下的直线方程转换到极坐标霍夫空间下，其极坐标的表达式为：

x×cos(θ)+y×sin(θ)=r

(2)

其中，r为原点到直线的距离；θ为原点到直线的垂直线的夹角.

在实现的图像处理领域，图像的坐标(x,y)是已知的，要根据每个(x,y)坐标求出(r,θ)，这种变换称为直线的霍夫变换.该变换是通过将霍夫参数空间量化为有限区间或者使用累加器单元叠加来实现.出现直线的依据就是累加器阵列产生了峰值，也就说明了图像中存在一组离散点可以拟合近似成一条直线.

1.2 去除连接特征

连接特征的检测要进行边缘检测，这里选择Canny边缘检测算法.Canny边缘检测是根据对信噪比与定位乘积进行测度，得到最优化逼近算子.其具体步骤描述为：

第一步：采用高斯滤波器方法进行去噪；

第二步：找到图像的强度梯度；

第三步：采用非最大值抑制的方法删除不属于边缘部分的像素；

第四步：选择上下阈值进行分割，确定潜在边缘；

第五步：去除不与强边缘相连接的所有弱边缘.

由于草图中直线特征并不全是连接特征，因此需要取一些连接特征共同的特点，设定一些阈值，将连接特征标记出来，具体做法为：首先在编程界面上手绘一个简单的电路草图样本(见图2)；然后选用Canny算法检测二值图像的边缘，并用蓝色的线段标记出来(见图3).设某一点的像素值为a(x,y)，二值图像的像素值a(x,y)={0,1}.连接特征的去除，只要将连接特征的像素值设与背景像素一致即可，即蓝色标记区域a(x,y)=0.去除连接特征后的电气原理图结果(见图4).

2 连通域分离技术

现阶段常用的图像分割技术大多是根据连通域特性来对简单的二值图像进行分割.由于草图中都是笔划，采用四连通域不包含所有的情况，故选用八连通域.先对草绘图像进行二值化处理，然后分析连通域，最后将单一连通域的区域分割出来.但是传统的连通域标记算法Suzuki标记算法耗时比较长，还会产生等价信息失效的问题,需要进行很多次的扫描进行改善，所以本文采用的是连通域标记改进算法[13].

2.1 传统的基于行程的连通域标记

传统的连通域标记算法大多采用的是基于行程的标记[14].这种算法的思想是逐行扫描图像，每一行中连续像素为0组成的一个序列为一个集合，并记下起点和终点以及行号.如果每一行中所有的集合与上一行一个集合有重合区域，则将上一行的标号赋给这个集合；如果它与上一行2个以上的集合有重叠区域，则给它赋一个相连集合的最小标号，并将上一行的这几个集合写入等价对，说明它们属于一类.将等价对转换为等价序列，每一个序列需要给一个相同的标号，因为它们都是等价.从1开始，给每个等价序列一个标号，遍历每个集合的标记，查找等价序列，给予它们新的标记，将每个集合的标号填入标记图像中.等价信息表(见图5).

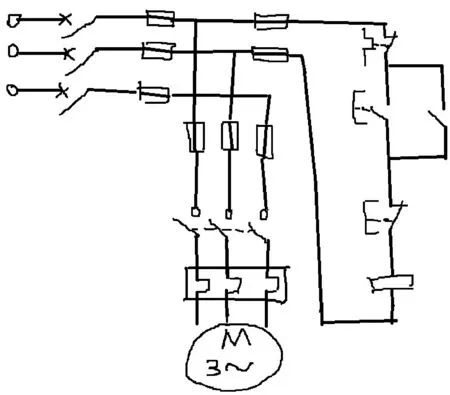
图2 手绘草图

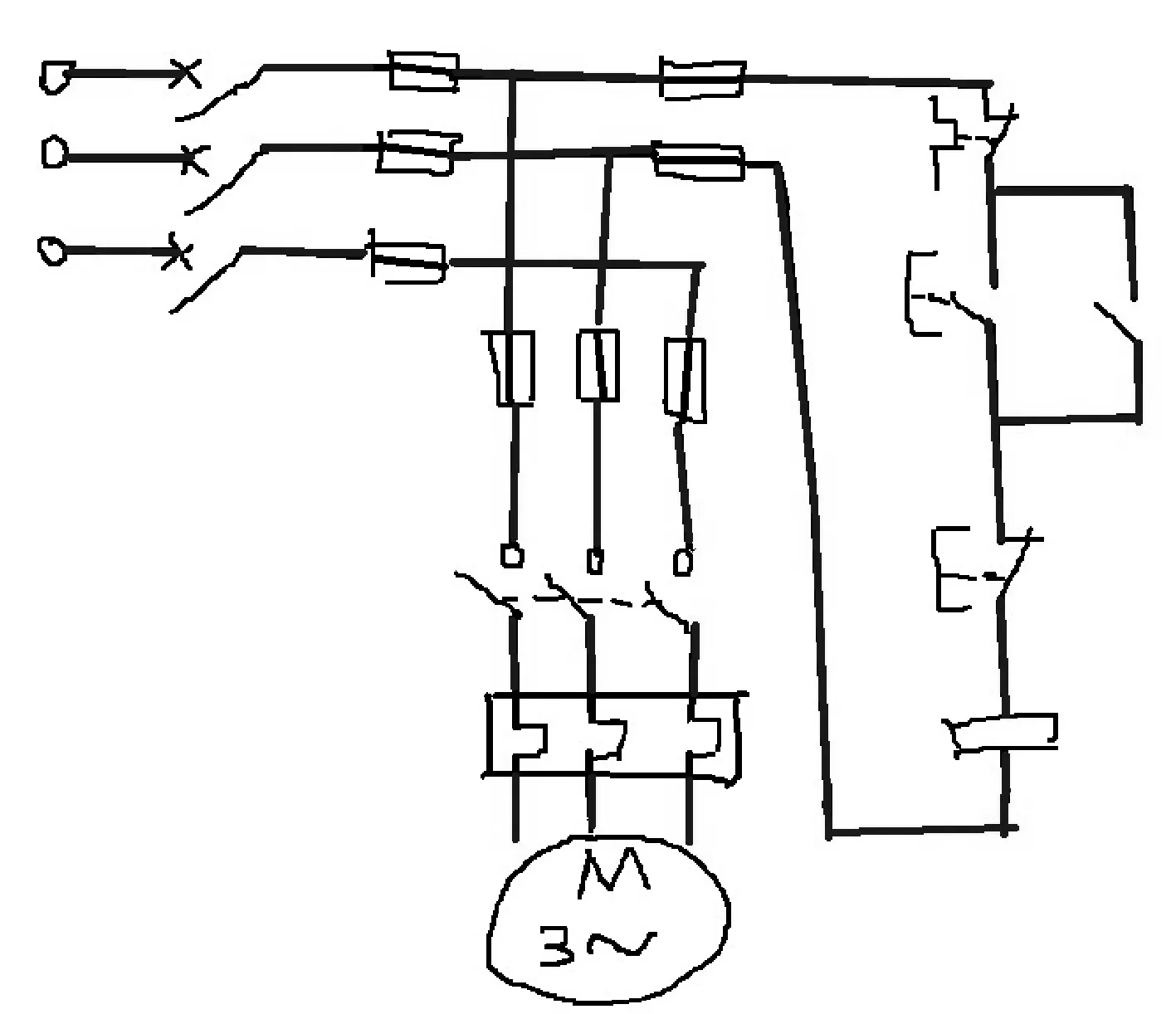
图3 霍夫直线识别

图4 去除连接特征图

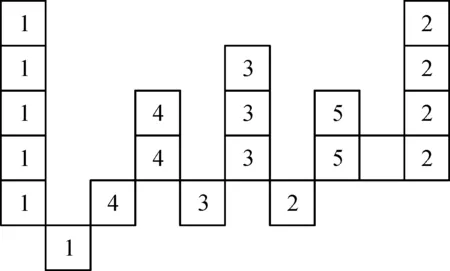
图5 等价信息表

设置初始标号m=1.对每个当前像素a(x,y)按下式计算其标号b(x,y).

(3)

Ms表示一个像素点的左、左上、上、右上的4个单元组成的区域.条件1表示a(x,y)为X；条件2表示当a(x,y)的Ms邻域中没有为X的值，则赋一个新值m，并且m比上一个新值增加1；条件3表示a(x,y)的Ms邻域中有为X的值，则赋上一行与之相连的最小值m.对于图中产生的等价对，要通过多次扫描,不停的更新标号，直到标号不再发生变化.

2.2 改进的连通域算法

传统的连通域标记算法之所以比较耗时，是因为更新像素标号的时候要经过多次扫描来更新图像.如果可以在扫描一次图像，记录像素标号的同时，能够依据上一行扫描的像素标号从后向前传播，并及时修改标号，这样就可以在一次扫描完图像，像素的标号也可以更新完毕，所以这里提出了一种改进的连通域标记算法.算法的思想是增加一步等价表T的标号的遍历，不用对整张图再扫描，比较节省时间.对T中的标号，选择一个根节点，记录该根节点的序号为α，在相同标号的T[α]分支上的邻域上，第一个大于T[α]的T[γ]标号记为T[α]，直到此分支结束，开始找到下一分支，再重复以上步骤.算法实现过程：

(1)设置一个用来记录标号的连接表为T，扫描图像遇到的第一个像素标号m=1.

(2)扫描图像的每一行，由式(3)计算出当前行中每个像素的标号g(x,y)，并按式(4)及时更新上一行的像素标号，这可以通过修改表T中的临时标号来完成.

(4)

(3)当扫描完图像，会产生这些节点的标号偏大，并且原始根节点的标号也不是最小标号，所以在这样一个类似于树形结构的标号表T中，需要增加一次对T的所有节点的临时标号更新，这里可使用树的深度优先遍历，可快速地更新所有在T中的标号至最小.

先将同一连通域的区域标注出来，用*号标记出来，图中共有24个部件，分析出来标记出31个*号，表明识别出来31个连通域(见图6).然后限定一个矩形，将这些区域用矩形标记出来，方便分割，找到连通域中像素点的最左、最右、最上、最下的位置，并以此做个矩形的区域，将连通域标记出来(见图7).

图6 连通域识别

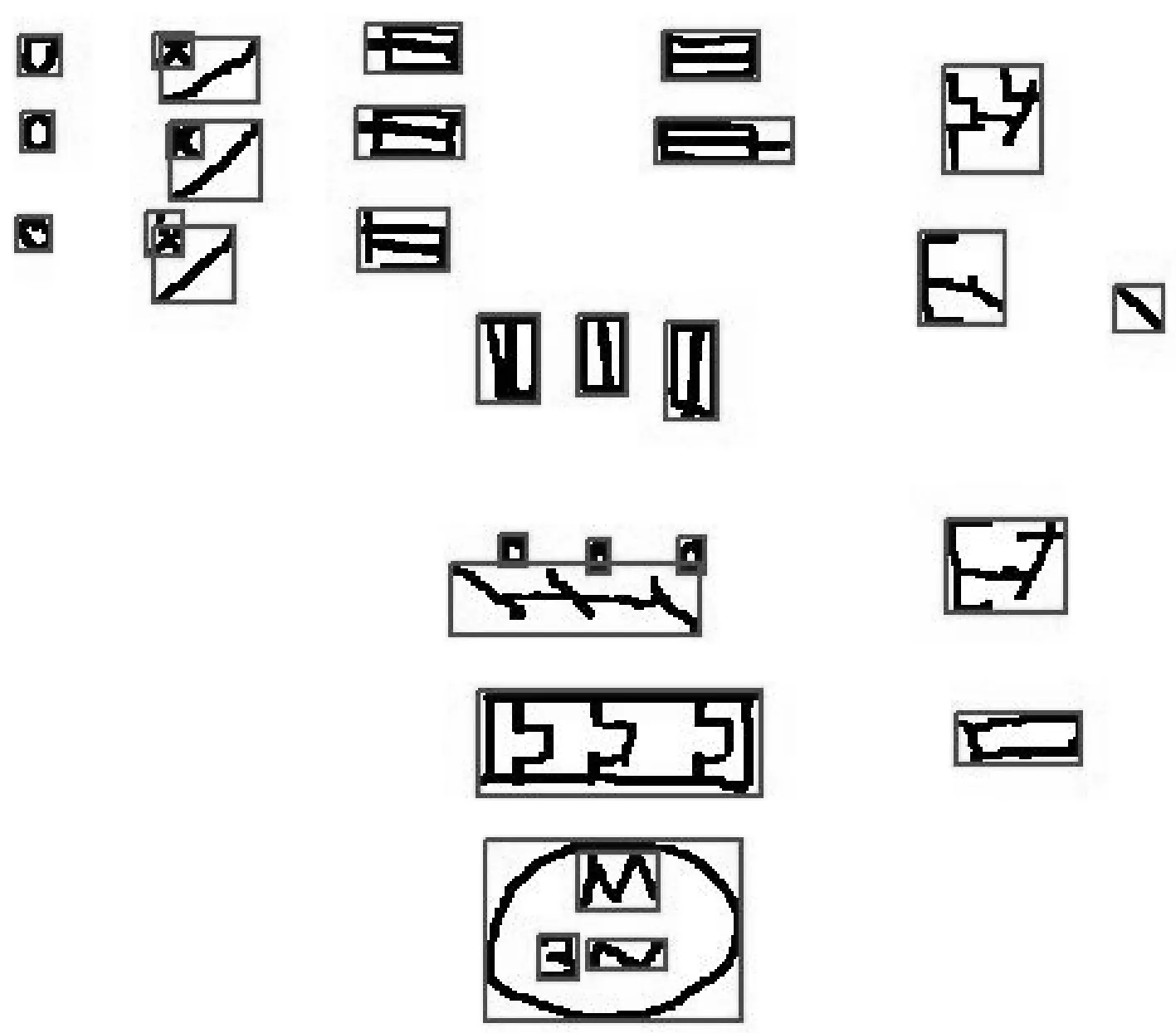
图7 连通域标记

2.3 合并相交区域

由于图中部分元器件是一个整体却被分割开来，那是因为图形在膨胀的过程中并没有将孔洞补上，从而产生结果上的不一致，故需要对分割出来的结果进行处理.对矩形框进行判别，对有相交区域的矩形进行合并，其步骤是：

(1)设计一个算法，确定两个矩形是否相交.

(2)如果两个矩形相交，设计一个算法，求出合并的最小矩形区域.

一般矩形相交有3种情况(见图8).其区域合并算法描述为：

第一步：输入两个矩形的左上角坐标(xa1,ya1)(xb1,yb1)和右下角坐标(xa2,ya2)(xb2,yb2).

第二步：判断max(xa1,xb1)<=min(xa2,xb2)和max(ya1,yb1)<=min(ya2,yb2)是否都成立.

第三步：如果第二步成立，则相交；反之不相交.

第四步：对相交的矩形进行合并处理.

根据上述算法进行区域合并以后，还需要将这些识别出来的一片片区域分割出来，达到每片区域都是一个单独的元器件的效果.

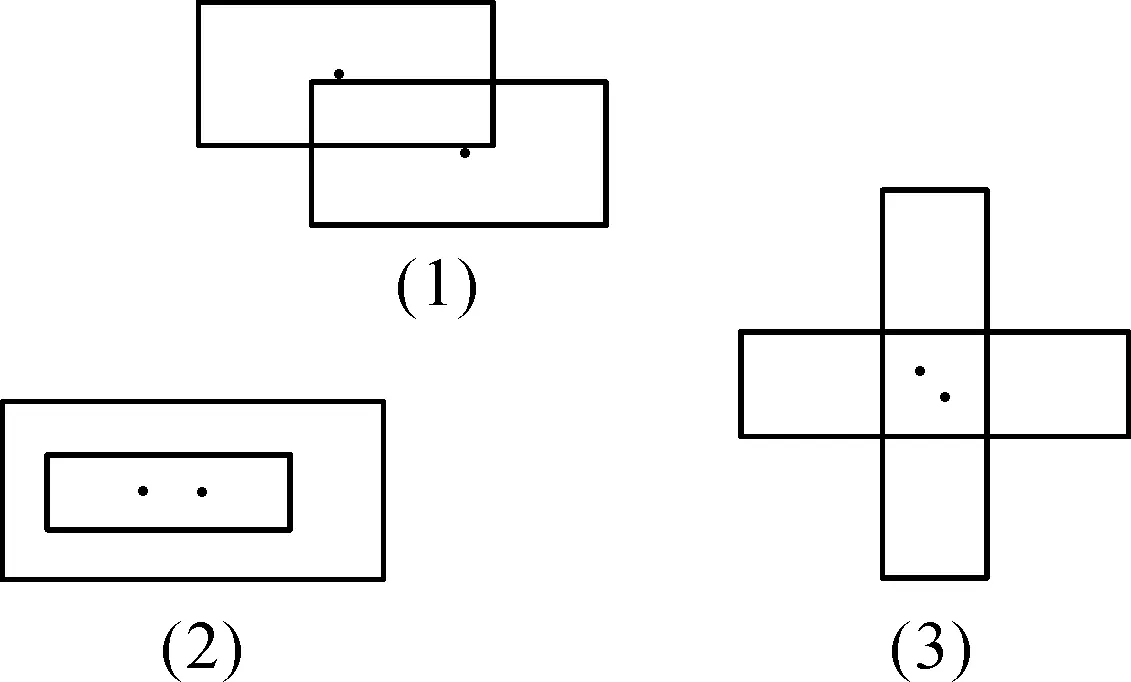
图8 矩形相交的3种情况

3 实验结果及分析

本文在Visual Studio 2013环境上(Intel CORE i7 CPU 5500U 2.40GHz CPU,4GB Memory, Windows 7)，利用C++语言编程对所提出的算法进行了验证与测试.测试图选择了手绘的两幅电气草图(见图9和图11)，最终分割结果(见图10和图12).在将分割出的区域还原到原草图结果中，得到的结果(见图12).最终的实验结果表明，原草图中所有的元器件的个数与分割出来的结果相一致，所以本文采用的分割方法可以有效地将每个元器件分割开来，而且具有良好的鲁棒性.

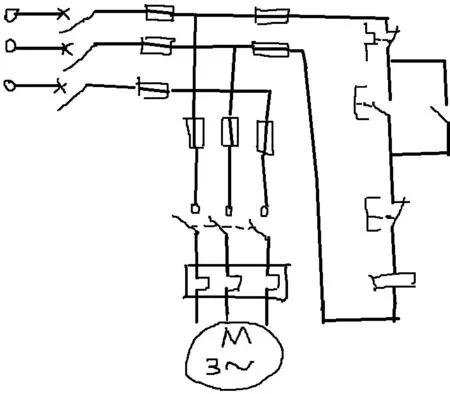
图9 手绘草图

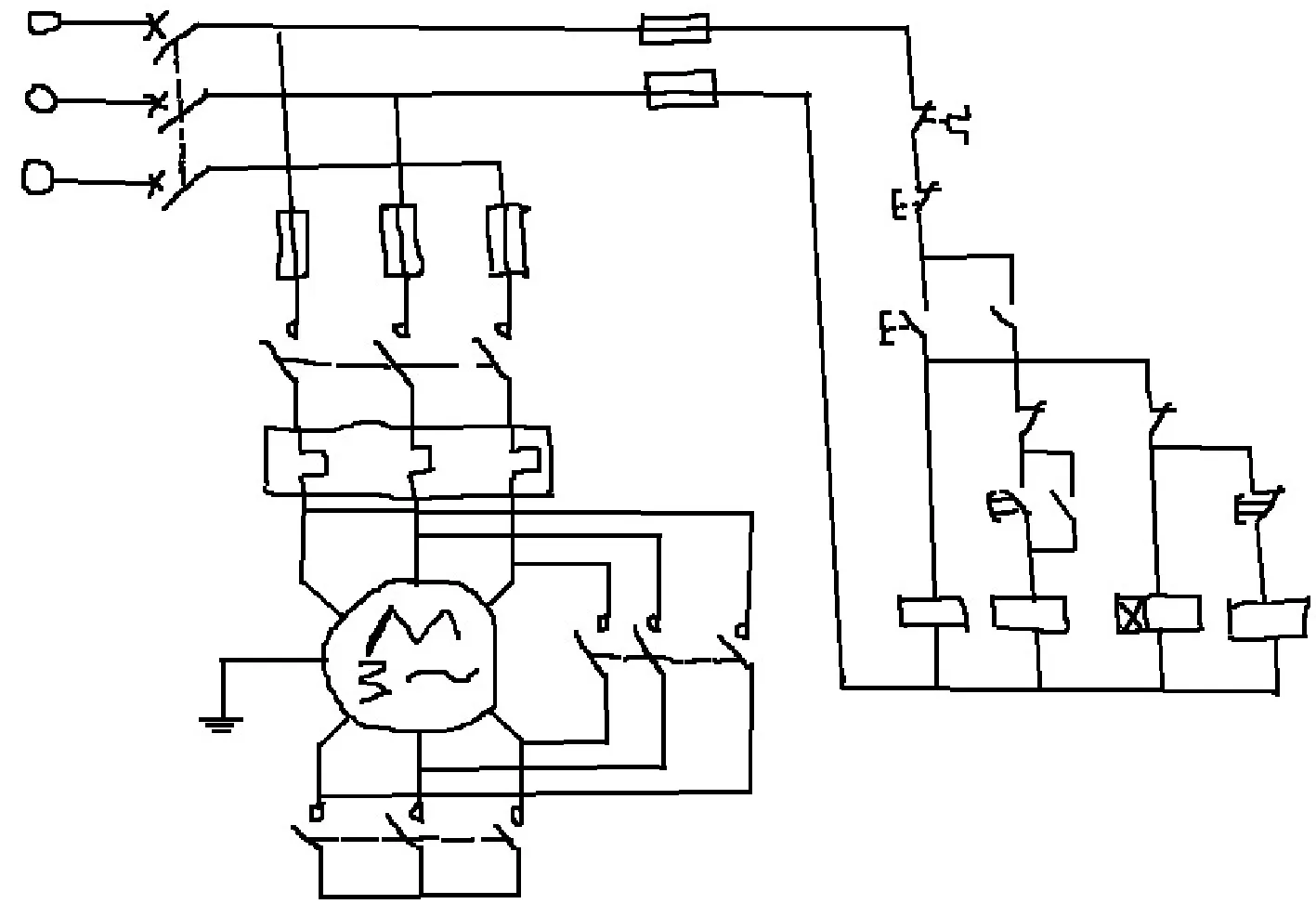
图10 手绘草图

图11 分割结果图

图12 分割结果图

为了测试本文算法在时间上的优化，对Suzuki标记算法与本文改进的算法在连通域识别上的时间进行了比较，所有数据都是测试100次之后在时间上的均值.测试图像是来自南加州大学的标准图像数据Miscellaneous database,Textures Database, Aerial Database的图像，并且选取的图像都是512×512、连通域最多的图形，其测试结果(见表1).

可以看到本文算法在相同图像下，时间上相较于传统的连通域标识算法缩短了约56%，并且可以很好地识别所有的连通域，可以看出减少扫描次数可以很好地降低时间复杂度，从而简化了算法的执行过程.

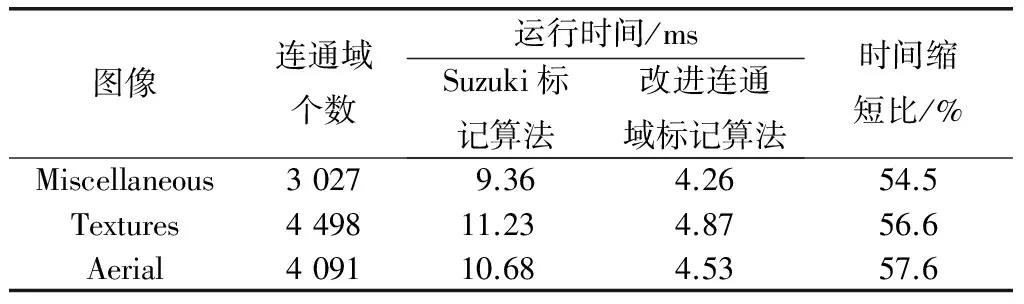
表1 两种算法的运行时间

4 结 语

针对草图的研究大多都集中在对单个草图符号的识别，很少从整体上对草图图像进行规划和整理.为了提高草图识别精确度，草图中符号分割具有重要意义.本文提出了一种可以连通域标识的改进算法，可以实现手绘电气原理图电气元器件符号的分割.传统算法是通过不断扫描图像，直到等价信息表不再发生变化为止，耗时较大.本文提出的算法只要添加一次对等价信息表的扫描就可以将最小标号传递，能够同样实现连通域的识别，而且通过减少扫描图像的次数，缩减了算法运行的时间.实验结果表明，该方法能够将草绘图中电气元器件符号进行有效地分割，并且在时间上也比传统的连通域标识算法缩短了约56%，从而提高算法运行的效率.

[1] CASELLES V,KIMMEL R,SAPIRO G. Geodesic active contours [J].International Journal of Computer Vision,1997,22(1):61-79.

[2] CASELLES V,CATTE F,COLL T,etal. A geometric model for active contours in image processing [J].Numerische Mathematik,1993,66(1):1-31.

[3] KICHENASSAMY S, KUMAR A, OLVER P,etal.Gradient flows and geometric active contour models [C]//IEEE International Conference on Computer Vision.Piscataway:IEEE,1995:810-815.

[4] ZHANG K,SONG H,ZHANG L. Active contours driven by local image fitting energy [J].PatternRecognition,2010,43(4):1199-1206.

[5] WANG Y,XIANG S,PAN C,etal. Level set evolution with locally linear classification for image segmentation [J]. Pattern Recognition, 2013,46(6):3361-3364.

[6] WANG L,LI C,SUN Q,etal. Active contours driven by local and global intensity fitting energy with application to brain MR image segmentation[J].Computerized Medical Imaging and Graphics,2009,33(7):520-531.

[7] KAPUR J N, SAHOO P K, WONG A K C. A new method for gray-level picture threshold using the entropy of the histogram[J]. Computer Vision, Graphics, and Image Processing, 1985, 29(3): 273-285.

[8] TSU N. A threshold selection method from gray level histogram [J].Automatica, 1975, 11(285-296): 23-27.

[9] FELZENSZWALB P,HUTTENLOCHER D. Efficient graph-based image segmentation[J]. International Journal of Computer Vision,2004,59(2):167-181.

[10] FOWLKES C.Spectral Grouping using the Nystrom method[J].IEEE Trans on PAMI,2004,26(2):214-255.

[11] HERNANDEZ-BELMONTE U H,AYALA-RAMIREZ V,SANCHEZ-YANEZ R E.A comparative review of two-pass connected component labeling algorithms[J].Advances in Soft Computing,2011,7095(12):452-462.

[12] GUIL N,VILLALBA J,ZAPATA E L.A fast hough transform for segment detection[J]. IEEE Transactions on Image Processing,1995,4(11):1541-1548

[13] SONKA M, HLAVV, BOYLE R. Image Processing analysis and machine vision,[2nd ed.][J].Journal of Electronic Imaging, 2008,xix(82):685-686.

[14] SUZUKI K,HORIBA I,SUGIE N.Linear-time connected component labeling based on sequential local operations[J]. Computer Vision and Image Understanding,2003,89(1):1-23.