基于Authorware三视图模拟识图系统的实现

王林玉

摘要

通过Authorware的图标化的编程方式，在Authorware中采用堆叠小立方体的方式，将15个小立方体随机填充到一个3*3*3的矩阵样式中，模拟空间的三维立体图形。在生成的模拟三维立体图形中，任选一个生成三视图，用热区响应的方式，选择与三视图对应的三维立体图形。实现三视图的模拟识图系统的制作，从而达到强化三视图识图的目的。

【关键词】Authorware 变量 函数 三视图

在机械零件图形绘制中，通常是用三视图来表达一个机械零件在各个面上的投影的轮廓形状。三视图一般指对象的主视图、左视图和俯视图，将机械零件用正投影法在三个相互垂直的投影面上产生的投影轮廓形状作为各自不同的投影图形，这种投影关系是一一对应的。CAD绘制三维图形时，常用的方法是将简单的二维图形，通过拉伸旋转和布尔运算之后，生成复杂的三维图形。对三视图的投影方法的理解以及三视图与三维图的对应关系，在工程绘图或CAD三维绘图都是很重要的一部分基础知识。在Authorware中用小立方体的方式构造空间立体，用堆叠立方体的方式构造空间物体。实现三视图识图系统的制作，通过使用此系统可以加强三视图识图能力的练习。

1系统设计思路

此练习系统中，采用小立方体单元堆叠的方式来构造网格式的空间立体对象，就象魔方玩具一样，空间立体对象是由3*3*3矩阵样式排列的小立体构成。系统中，用15个小立方体随机填充到不同的位置，就能构造出结构复杂又变化多样的空间立体，在系统界面中，每次构造6个立体对象，处于不同的位置而且每组随机取出一个立体构造其三视图。

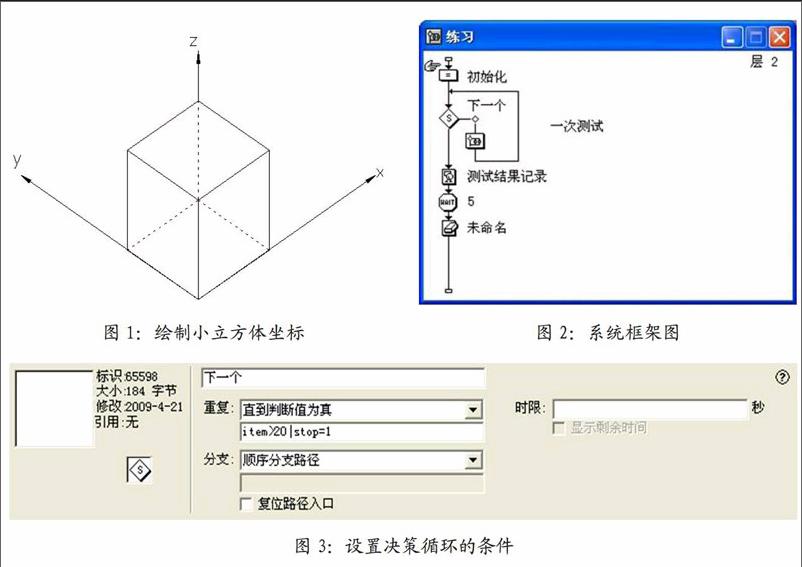
用堆叠小立方体的方式构造空间立体时，从不可见的面向可见面堆叠。对于空间小立方体的绘制，建立一个用户坐标系，确定基点坐标及各个坐标轴方法（图1绘制小立方体坐标）。根据坐标轴的方向，在绘制空间立体各个小立方体单元，绘制时要按照从下向上（z坐标）、从右向左（y坐标）、从后到前（x坐标）的顺序来绘制，这样使空间位置靠前的小立方体能够遮住后面的小立方体。其中靠前的小立方体遮住后面的小立方体部位不可见的线，用白色的线条绘制。

在垂直于投影面的一列网格单元中，只要有一个位置被填充了小立方体，这列网格对应的投影位置就应出现一个小矩形。

制作此系统，首先建立基本的程序结构和界面，如图2所示。

在初始化中，设置变量stop和分组变量item设置初始值，设置stop：=0，item：=l。在决策图标的属性窗口，选择循环属性为直到判断值为真，并定义退出的条件为item>20|stop=1，这样，当分组变量item达到20或者停止标志变量stop被置为1，都将结束这个决策循环，如图3所示。

2系统实现过程

打开群组图标，在一次测试流程图中，设置分支结构如图4所示。

2.1随机构造空间立体

在分支中，六次决策图标和之下的群组图标，用来在窗口中生成随机构造空间立体堆。其分支结构中，分别用三个计算机图标，依次为生成“立方体”、“画立方堆”、“下一个立方堆”来顺序执行。其后跟一个决策图标“选择立方堆”。

其中，“生成立方体”计算图标中，利用数组记录3*3*3矩阵网格各立方体填充情况，先对数组初始化，程序代码为：

Repeat with x：=lto3

Repeat with y：=lto3

Repeat with z：=lto3

E1：=x*100+y*10+z

Arrayset（el，0）

End repeat

End repeat

End repeat

N：=l

Repeat while n<=15；利用变量n控制总数不超过15个

Rx：random（l，3，l）；为变量rx随机选择一个1-3之間的整数

Ry：=random（l，3，l）；为变量ry随机选择一个1-3之间的整数

If arrayget（rx*100+ry*10+l）=0then

Arrayset（rx*100+ry*l0+1，1）；判断代表网格单元的数组元素值是否为0，是则将其值置为1

Else

If arrayget（rx*100+ry*10+2）=0 then

Arrayset（rx*100+ry*10+2，1）

Else

If arrayget（rx*l00+ry*10+3）=0 then Arrayget（rx*100+ry*10+3，1）

Else

N：=n-1

End if

End if

End if

N：=n+1

End repeat

在计算图标“画立方堆”中，输入如下程序

Sx：=mot（keer，3）*130+80；用变量keer和mod函数、int函数确定空间立体的起始点坐标

Sy：=int（keer/3）*130+190Repeatwithz：=lto3按照Z坐标、Y坐标、X坐标的顺序绘制前面随机确定的小立方体。

Repeat with y：=3 down to 1

Repeat with x：=3 down to 1

If arrayget（x*l00+y*10+z）=l then 如果数组元素的值为1，该元素对应的空间立体单元位置有一个小立方体，因此进入绘制程序Cx：=sx-（y-x）*17

Cy：=sy-（x+（y-z））*10-（z-l）*30；确定基点坐标endprint

Setfame（l，rgb（255，255，255））；使用白色的线条绘制不可见部分

Line（1，cx，cy-20，cx-17，cy-10）

Line（1，cx+17，cy-10，cx，cy-20）

Linet）1，cx，cy-40，cx，cy-20）

Setframe（l，rgb（255，0，0））；用紅色绘制小立方体顶面的4条边

Line（1，cx，cy-20，cx-17，cy-30）

Line（1，cx，cy-20，cx+17，cy-30）

Line（l，cx-17，cy-30，cx，cy-40）

Line（l，cx+17，cy-30，cx，cy-40）

Setfame（l，rgb（0，255，0））；用绿色绘制左侧面的边

Line（1，cx，cy，cx-17，cy-10）

Line（1，cx-17，cy-10，cx-17，cy-30）

Line（1，cx，cy，cx，cy-20）

Setframe（l，rgb（0，0，255））；用蓝色绘制前面的边

Line（1，cx，cy，cx+17，cy-10）

Line（1，cx+17，cy-10，cx+17，cy-30）

End if

End repeat

End repeat

End repeat

在流程线上加一个计算图标“下一个立方体”，将位置变量keer：=keer+l，在下一个循环中在下一个位置绘制另一个空间立体。

2.2随机选择空间立体构造三视图

在第四层流程图中加入一个决策图标，设置分支属性为to calculated path，定义计算表达式为“keer=w”，由于变量keer是递增的，而变量W是前面产生的随机值，因此这样设置可以随机选择一个空间立体。

在群组图标流程线上，加入三个计算机图标，分别用来判断小立方体是否在某一个面上有投影。其中实现程序如下：

Vaz：=””

Repeatwithz：=3downto1

Repeat with x：=l to 3

K：=arrayget（x*100+10+z*l）+arrayget（x*100+20+z*l）+arrayget（x*100+30+z*1）

If k>0 then vaz：=vaz∧l else

vaz：=vaz∧0

End repeat

End repeat

判断某一列是否有小立方体单元：将该列三个单元对应的数组元素的值相加，如果和大于0，说明有小立方体，同时为字符串变量vaz添加字符1，否则添加字符0。其它两个视图程序相同。

在第三层流程线上，用一个群组图标，加入显示图标和三个计算图标，用来设置图形的显示和绘制，其实现程序如下：

在程序中，利用函数substr从字符串变量vaz中取出前3个字符，中间3个字符和最后3个字符，并分别赋值给3个字符串变量，绘制最上面的一排单元格，如果字符为1，说明需要绘制小方块，边长设置为15，否则不绘制。绘制中间一排的单元格，小方块的Y坐标增加15，然后绘制最下面一排单元格，小方块的Y坐标再增加15。同理，绘制其它两个视图。

2.3判断及统计

在系统设计后期，需要提示用户要完成的任务。然后利用热区响应判断用户选择的是否正确，是则继续下组练习，否则重新选择，记录选择的正误次数，结束程序时显示练习情况。具体的做法为如下：

（1）在流程图上加入一个交互图标，其下加入两个计算图标，用按钮响应，分别为返回和下一组练习。加入两个群组图标，分别是正确的选择和错误的选择，用热区响应。

（2）在正确的选择群组图标中，设置其分支流向为离开交互，在错误的选择分支中设置其流向为返回。

（3）在每次正确选择之后，用擦除图标来擦除正确提示信息。

其流程图如图5所示。

系统设计最后效果如图6所示。

3结论

系统的设计与实现，首先是用数组记录空间立体构造情况，随机为数组元素赋值。然后根据数组元素值，在对应位置绘制小立方体单元，随机选个空间立体，用字符串变量记录其在各投影面的投影情况，根据字符串变量的值绘制三视图，利用热区响应判断用户选择是否正确，统计测试情况。

参考文献

[1]宋一兵，迟洁茶.Authorware6典型应用实例与技巧[M].北京：人民邮电出版社，2002.

[2]许永年，覃小斌.工程制图[M].北京：中央广播电视大学出版社，1999.endprint