基于DSR Time-Sweep的沥青常应变疲劳演化规律分析
朱洪洲,范世平,卢章天
(1.山区道路结构与材料重庆市重点实验室,重庆 400074;2.重庆交通大学 土木工程学院,重庆 400074;3.广西交通规划勘察设计研究院有限公司,广西 南宁 530029)
0 引 言
疲劳性能表征材料在重复荷载作用下抵抗破坏的能力。由于超载、重载现象的增加和沥青路面结构自身设计不足,使疲劳破坏成为目前沥青路面主要损坏形式之一,也是沥青路面结构设计和沥青混合料组成设计研究的重点。沥青混合料是由沥青胶浆和矿质集料拌和而成,经研究发现[1-3],沥青路面疲劳裂缝一般产生于沥青胶浆内部或沥青与集料黏结界面,表明沥青混合料疲劳性能主要依赖于混合料中沥青疲劳性能,因此在研究沥青混合料疲劳性能之前先对沥青疲劳性能研究是很有必要的。
沥青材料在通常情况下属于黏弹性材料,沥青的疲劳破坏是个较为复杂的过程。随着动态剪切流变仪(DSR)的发展,国内外学者采用动态剪切流变仪,通过不同加载方式对沥青疲劳性能及影响因素做了大量研究[4-13]。但现有研究主要集中在某一沥青胶浆或沥青混合料疲劳性能评价指标和疲劳方程的统一,对多种沥青在重复荷载作用下疲劳破坏变化规律研究较少。此外,国内外对沥青疲劳性能的研究尚未得出统一、合理的评价指标,鉴于此,笔者采用动态剪切流变仪(DSR),在应变控制模式下对70#基质沥青和SBS改性沥青进行重复剪切疲劳试验,分析70#基质沥青和SBS改性沥青在常应变控制模式下的疲劳演化规律。研究成果可为沥青或沥青混合料疲劳指标的建立提供理论依据。
1 试验材料与方法
1.1 试验材料
本研究选用常用的70#基质沥青和SBS改性沥青,其技术指标见表1和表2。

表1 70#基质沥青技术指标Table 1 Technical indicators of 70 # base asphalt
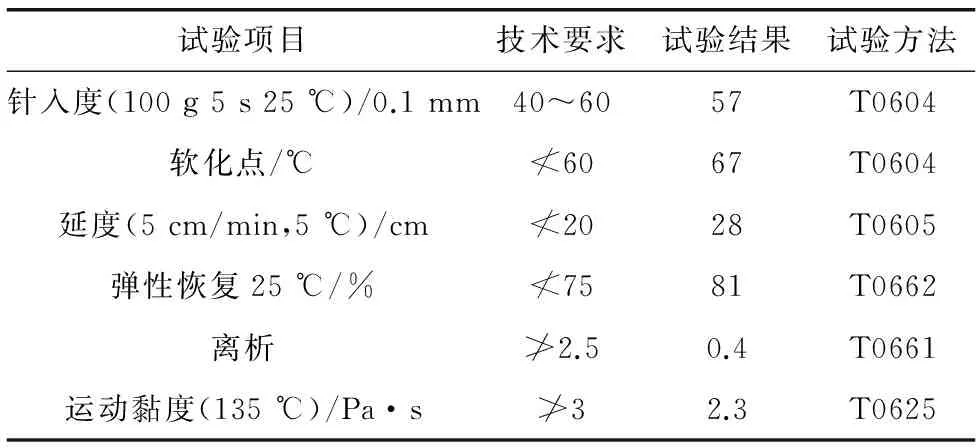
表2 SBS改性沥青技术指标Table 2 Technical indicators of SBS modified asphalt
1.2 试验方法
本研究试验均采用动态剪切流变仪(DSR)的时间扫描模式。平行板夹具直径8 mm;加载频率10 Hz;试验发现,在15或20 ℃温度环境中进行疲劳试验时会出现沥青与平行板黏结不牢固的问题,导致沥青与平行板的黏结界面发生破坏,而非沥青自身疲劳破坏,从而影响试验结果,当试验温度为30 ℃时,沥青试样具有良好的疲劳破坏形态,因此本试验温度采用30 ℃;疲劳试验在应变控制模式下进行,70#基质沥青和SBS改性沥青应变水平分别为5%、8%、10%和8%、10%、12%。
2 试验结果与分析
2.1 复数剪切模量G*随荷载作用的变化规律
复数剪切模量(G*)表示沥青在重复荷载作用过程中抵抗剪切变形能力的大小,由弹性和黏性两部分组成,其黏、弹性能相对关系用相位角δ表示。复数剪切模量越大,表示沥青抵抗剪切变形能力越强。通过复数剪切模量随荷载作用次数的变化关系,可以得出沥青疲劳破坏发展规律。图1表示70#基质沥青和SBS改性沥青复数剪切模量(G*)随加载次数(N)的变化关系(G*-N曲线)。

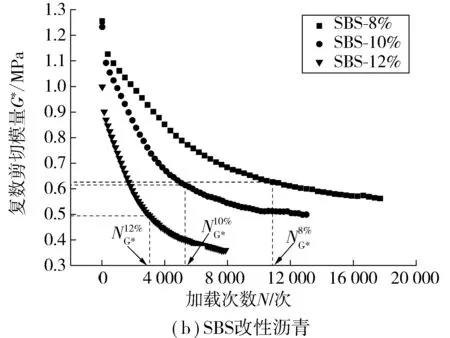
图1 复数剪切模量随加载次数变化关系Fig. 1 Relationship between complex shear modulus with loading times
由图1可见,两种沥青的复数剪切模量均随着荷载作用次数的增加而减少,但二者递减规律有显著差异。对于70#基质沥青,在荷载作用初期,沥青处于荷载适应阶段,复数剪切模量下降缓慢;随着荷载作用次数的增加,沥青内部微损伤开始快速发展直至破坏,故该时期复数剪切模量衰减速率大;在常应变控制模式下,随着荷载的不断作用,沥青抵抗剪切变形能力降低,为了保持应变恒定,必须减小作用应力大小,因此常应变控制模式下沥青通常不会发生完全破坏。故G*-N曲线在荷载作用后期会出现趋于稳定不变的趋势。可将70#基质沥青疲劳破坏阶段分为3个阶段,即初始适应阶段,快速发展阶段和稳定阶段。此外,当复数剪切模量下降到初始值50%时处于快速发展阶段后期,沥青疲劳程度不断加深接近完全破坏,将该点定义为70#基质沥青疲劳寿命破坏点,其对应的荷载作用次数记为沥青疲劳寿命NG*。与70#基质沥青相比,由于改性剂改善了沥青黏弹性能,SBS改性沥青G*-N曲线不存在初始适应阶段,随着荷载不断作用,复数剪切模量迅速下降进入稳定阶段。同70#基质沥青,将初始复数剪切模量下降至50%时对应的加载次数定义为沥青疲劳寿命。
同种沥青在不同应变水平下G*-N曲线变化趋势相同,且应变越大,复数剪切模量衰减越快,疲劳寿命越短。
2.2 累计耗散能比(DER)随荷载作用的变化
假定每个荷载作用周期内材料的损伤都小到忽略不计,即每个荷载作用周期产生的耗散能wi是恒定的,令wi=wn,则累计耗散能和累计耗散能比见式(1)、式(2):
(1)
(2)
结合式(1)、式(2)可看出,当材料损伤程度很小或者没有损伤时,累计耗散能比DER就等于加载次数N,当材料在N+1次产生损伤时,由于新的损伤消耗了能量,即wi将不再保持恒定,即DER与N的差值将增大。图2为70#基质沥青和SBS改性沥青的累计耗散能比DER与加载次数N的变化曲线(DER-N曲线)。
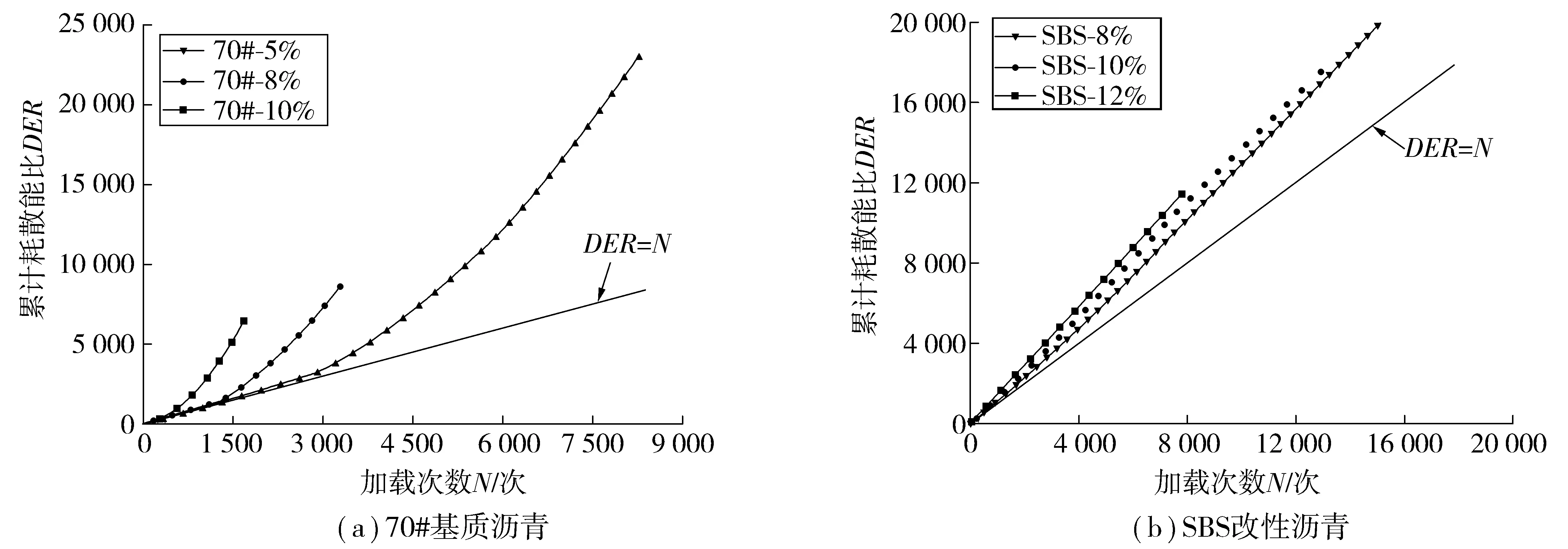
图2 累计耗散能比随加载次数变化规律Fig. 2 Law of cumulative dissipative energy ratio changing with loading times
由图2可见,在荷载作用初期,两种沥青的DER-N曲线近似于直线DER=N,表明沥青内部尚未发生损伤或者损伤很小;随着荷载作用次数增加,DER值加速增大,DER-N曲线偏离直线DER=N,此时沥青内部产生损伤并不断扩展。由于DER-N曲线无明显转折点,因此无法直接定义沥青疲劳寿命。A. C. PRONK等[14]提出从DER-N曲线末端做切线与直线DER=N相交,以交点所对应的加载次数作为沥青疲劳寿命,但由于在应变模式下,沥青很难发生完全破坏,因此DER-N曲线末端的加载次数取决于停止施加荷载作用的时间点。笔者研究发现,相同条件下选取的总荷载作用次数越大,DER-N曲线末端切线与DER=N直线交点所对应的加载次数就越大,表明以Pronk理论定义沥青疲劳寿命依赖于总荷载作用次数,即疲劳寿命依赖沥青的损伤程度。笔者重点在于研究常应变控制模式下沥青疲劳寿命演化规律。因此,为了使分析结果具有对比性,统一以沥青达到相同损伤程度时所对应的荷载作用次数作为总荷载次数,在按照Pronk理论确定沥青疲劳寿命。笔者选取复数剪切模量下降为初始值的30%时对应的荷载作用次数作为总荷载次数,并按照Pronk理论确定疲劳寿命。
2.3 耗散能变化率(DR)随荷载作用的变化规律
沥青的疲劳破坏,必然伴随着能量的耗散,这部分能量包括破坏过程中黏性和弹性部分共同产生的能量。且能量变化伴随整个破坏过程,通过耗散能变化可以很好的分析沥青疲劳破坏规律。耗散能变化率是指相邻加载周期内能量耗散速率,具体见式(3)、式(4):
(3)
ωi=πεσsinδ=πε2G*sinδ
(4)
式中:DR为耗散能变化率;wi为第i次荷载作用中耗散的能量,N·m;wi-1为第i-1次荷载作用中耗散的能量,N·m;G*为复数剪切模量, MPa;δ为相位角。
在荷载作用初始阶段,沥青在每个荷载作用周期内基本没有发生损伤或者损伤较小,即每个荷载作用周期内能量基本保持恒定;随着荷载的不断作用,沥青发生疲劳破坏并不断发展,耗散能变化率增大。因加载过程中应力逐渐减小,导致每个荷载作用周期内耗散能减少,即DR<0。
相关研究显示[6],在应变模式下,沥青的耗散能变化率DR值随荷载作用次数N的变化是杂乱无章的,不存在明显的曲线关系,试图通过DR-N分布图表征沥青疲劳寿命几乎是无法实现的。但笔者研究中发现,DR值随加载次数变化的分布趋势与沥青种类有关。根据试验结果,70#基质沥青和SBS改性沥青的DR-N分布图截然不同,如图3。

图3 耗散能变化率随加载次数变化规律Fig. 3 Law of dissipative energy variation ratio changing with loading times
从图3可见,随着荷载的不断作用,70#基质沥青的DR值先增大后减小,再增大后趋于稳定,DR-N曲线中先后出现了两个转折点,第1个转折点之前是沥青疲劳试验的适应阶段,第2个转折点之后是沥青疲劳破坏阶段,两个转折点之间是疲劳破坏发展阶段。将第2个转折点对应的加载次数作为70#基质沥青的疲劳寿命。且控制应变越大,沥青疲劳寿命越短。
与70#基质沥青相比,SBS改性沥青的DR值随加载次数分布的离散性强,数据波动大,DR与N之间无法形成清晰的曲线关系。且DR值随荷载作用增加呈逐渐增大趋势,表明沥青处于疲劳发展阶段,无法据此明确定义沥青疲劳寿命。因此根据DR-N分布无法确定SBS改性沥青的疲劳寿命。
3 基于不同分析的沥青疲劳寿命
3.1 不同沥青疲劳寿命对比
图4表示应变分别为8%和10%时基于复数剪切模量和累计耗散能比所获得的70#基质沥青和SBS改性沥青疲劳寿命对比。

图4 不同指标的沥青疲劳寿命对比Fig. 4 Comparison of asphalt fatigue life based on different indexes
从图4可见,在同一应变水平下,SBS改性沥青疲劳寿命明显优于70#基质沥青,SBS改性沥青与70#基质沥青疲劳寿命之比高达5∶1。究其原因,主要是由于改性剂改善了沥青黏弹性能,提高沥青弹性恢复能力,从而提高沥青承受荷载作用次数,使沥青疲劳寿命增强。
3.2 沥青疲劳寿命方法对比
相关研究表明[15-16],沥青DSR疲劳试验的疲劳寿命与加载应变之间服从对数线性关系,通常可以用式(5)表示:
(5)
式中:Nf为沥青的疲劳寿命,次;γ为试验中施加的应变大小;K、b为回归系数。
K值越大,表示沥青疲劳寿命越好;b值表示疲劳曲线的陡缓程度,b值越大,表示沥青疲劳寿命对应变越敏感,疲劳寿命越低。70#基质沥青和SBS改性沥青疲劳寿命与应变大小在双对数坐标中的变化关系如图5。

图5 疲劳寿命与应变大小双对数关系Fig. 5 The double logarithmic relation between fatigue life and strain
从图5可知,70#基质沥青疲劳方程中K值最大的是NDR,其次是NG*,NDER最小。而SBS改性沥青却恰恰相反,即NG*的K值最小,NDER的K值最大;b为正值,沥青疲劳寿命与应变水平有很大关系,疲劳寿命随着应变水平的增加而降低。
如图5所示,应变控制模式下,70#基质沥青由DER方法确定的疲劳寿命小于50%G*方法确定的疲劳寿命,而对于SBS改性沥青,试验结果相反。根据前文分析可知,DER方法确定的沥青疲劳寿命取决于停止荷载作用时沥青承受的总荷载次数,因此在总荷载作用次数未知情况下,不易采用DER方法确定沥青疲劳寿命。同时,虽然G*-N曲线能较好表征沥青疲劳演化规律,但50%G*方法确定沥青疲劳寿命是经验性的,随机性较大。与50%G*方法相比,DR方法是根据沥青疲劳曲线的转折点确定沥青疲劳寿命,定义明确、合理,但DR方法无法确定应变模式下SBS改性沥青疲劳寿命。综上所述,在应变控制模式下,G*-N曲线能较好表征沥青疲劳破坏规律,50%G*方法确定沥青疲劳寿命不受沥青种类和加载次数的限制,但其合理性有待商榷;DER方法确定的沥青疲劳寿命虽不受限于沥青种类,但取决于荷载作用总次数;DR方法确定沥青疲劳寿命定义明确、合理,但其应用受到沥青种类限制,无法用于确定SBS改性沥青疲劳寿命。
4 结 论
1) 沥青疲劳曲线变化规律受沥青种类影响较大,在笔者所采用的疲劳破坏分析方法中,70#基质沥青的疲劳曲线变化规律明显,曲线中有明确表示沥青发生疲劳破坏的突变点,而SBS改性沥青由于改性剂改变了沥青黏弹性能,在加载过程中,沥青弹性恢复能力加强,使疲劳曲线变化规律不显著。
2) 耗散能变化率可以表征70#基质沥青疲劳破坏变化规律,DR-N曲线存在两个转折点,可将第2个转折点对应的荷载作用次数作为沥青疲劳寿命。但耗散能变化率无法表征在SBS改性沥青的疲劳演化规律。
3) 累计耗散能比能用于确定沥青疲劳寿命,随着荷载作用次数的增加,沥青累计耗散能比增大,在加载总次数确定条件下,可将DER-N曲线末端引切线与DER=N直线的交点对应加载次数作为沥青疲劳寿命。
4) 在应变控制模式下,50%G*方法确定沥青疲劳寿命不受沥青种类和加载次数的限制,但其合理性有待商榷;DER方法确定的沥青疲劳寿命虽不受限于沥青种类,但取决于荷载作用总次数;DR方法确定沥青疲劳寿命定义明确、合理,但其应用受到沥青种类限制。
本研究主要针对连续加载模式下沥青疲劳寿命进行分析,但并未考虑沥青在加载过程中发生自愈合所带来的影响,今后将进行相关试验加以研究。
[1] LIAO M C,CHEN J S,TSOU K W.Fatigue characteristics of bitumen-filler mastics and asphalt mixtures[J].JournalofMaterialsinCivilEngineering,2002,24(7):916-923.
[2] KIM Y R,LITTLE D N,SONG I.Effect of mineral fillers on fatigue resistance and fundamental material characteristics:mechanistic evaluation[J].TransportationResearchRoad, 2003,1832(1):1-8.
[3] TAN Y,SHAN L,LI X.Fatigue characteristic of asphalt[J].GeotechnicalSpecialPublication,2008,182:98-107.
[4] 袁燕.改性沥青胶浆的疲劳性能评价[D].广州:华南理工大学,2005.
YUAN Yan.EvaluationofFatiguePerformanceofModifiedAsphalt[D].Guangzhou:South China University of Technology,2005.
[5] MASAD E,CASTELO BARNCO V T F,LITTLE D E,et al.A unified method for the analysis of controlled-strain and controlled-strain fatigue testing[J].InternationalJournalofPavementEngineering,2008,9(4):233-246.
[6] YU J M,TSAI B W,ZHANG X N,et al.Development of asphalt pavement fatigue cracking prediction model based on loading mode transfer function[J].RoadMaterials&PavementDesign,2012,13(3):501-517.
[7] 高爽.沥青混合料疲劳损伤机理研究[D].重庆:重庆交通大学,2008.
GAO Shuang.ResearchonFatigueDamageMechanismofAsphaltMixture[D].Chongqing:Chongqing Jiaotong University,2008.
[8] 姜睆.沥青胶浆自愈合能力研究[D].武汉:武汉理工大学,2011.
JIANG Huan.StudyonSelf-healingAbilityofAsphalt[D].Wuhan:Wuhan University of Technology,2011.
[9] 徐辰.沥青自愈合特性及影响因素研究[D].重庆:重庆交通大学,2013.
XU Chen.StudyonCharacteristicsandInfluencingFactorsofAsphaltSelf-Healing[D].Chongqing:Chongqing Jiaotong University,2013.
[10] 孙大权,林添坂,曹林辉.基于动态剪切流变试验的沥青疲劳寿命分析方法[J].建筑材料学报,2015,18(2):346-350.
SUN Daquan,LIN Tianban,CAO Linhui.Evaluation method for fatigue life of asphalt based on dynamic shear rheometer test[J].JournalofBuildingMaterials,2015,18(2):346-350.
[11] 陈浩浩,吴少鹏,刘全涛,等.沥青的疲劳性能评价方法研究[J].武汉理工大学学报,2015,37(12):47-52.
CHEN Haohao,WU Shaopeng,LIU Quantao,et al.Study on evaluation methods for fatigue property of asphalt[J].JournalofWuhanUniversityofTechnology,2015,37(12):47-52.
[12] BAHIA H U,ZHAI H,ZENG M,et al.Development of binder specification parameters based on characterization of damage behavior[J].JournaloftheAssociationofAsphaltPavingTechnologists,2002,70:442- 470.
[13] BONNETTI K,NAM K,BAHIA H.Measuring and defining fatigue behavior of asphalt binders[J].JournaloftheTransportationResearchBoard,2002,1810(1):33- 43.
[14] PRONK A C,HOPMAN P C.Energy dissipation:the leading factor of fatigue[C]//HighwayResearch:SharingtheBenefits.London:[s.n.],1991.
[15] 刘全涛.沥青胶浆的疲劳性能研究[D].武汉:武汉理工大学,2008.
LIU Quantao.StudyonFatiguePerformanceofAsphalt[D].Wuhan:Wuhan University of Technology,2008
[16] 吴少鹏,江承建,林俊涛,等.老化沥青胶结料的疲劳特性研究[J].武汉理工大学学报(交通科学与工程版),2013,37(3):451- 455.
WU Shaopeng,JIANG Chengjian,LIN Juntao,et al.Study on fatigue properties of aged asphalt binder[J].JournalofWuhanUniversityofTechnology(TransportationScienceandEngineering),2013,37(3):451- 455.

