新型双轴电容式加速度传感器设计*

朱彬彬，王路文，汶 飞，王高峰

(杭州电子科技大学 微电子CAD研究所，浙江 杭州 310018)

0 引 言

电容式加速度计因体积小、灵敏度高、易制造和低功耗等特点而被广泛应用[1～3]。传统加度速计多为单轴，不利于实际应用。因此，实现多轴测量及提高结构精度，成了设计的关键点[4]。实现多轴加速度计有两种方法：1) 将两个单轴传感器集成到一起形成双轴传感器;2)仅用一个质量块，实现多轴检测。和前者相比，后者具有更小的芯片面积及更低功耗[5]。Jayanetti V C等人提出了一种基于电容式的二自由度MEMS加速度传感器[6]，该结构由一组蛇形梁支撑一个X型对称质量块实现。Serrano-Vazquez F X等人阐述了一种通过单质量块实现垂直两轴加速度检测的结构[7]。

本文研究的双轴加速度计仅用一个敏感结构实现了两个方向加速度的检测，通过这种方法能有效避免因为跨轴而形成的干扰问题。且由于采用体硅工艺制作加速度计，得到了大的质量块，提高了灵敏度。仿真结果显示加速度计X轴和Y轴的位移灵敏度分别为0.084 5 μm/gn和0.138 1 μm/gn。

1 理论分析

1.1 加速度传感器工作原理

微机电系统(micro-electro-mechanical system,MEMS)加速度传感器可以简化为一个质量—阻尼—弹簧系统，如图1所示。当外界加速度作用于质量块时，根据牛顿第二定律可以将该力学模型表达为

(1)

式中m，b，k分别为质量、阻尼系数以及弹性系数；x(t)为质量块的相对位移；a(t)为输入加速度。

从式(1)中得知，通过测量质量块的位移可以实现加速计的检测。系统处于常加速度输入的稳定状态时，式(1)可变换为

(2)

图1 质量—阻尼—弹簧系统

从式(2)可见，对于加速度传感器来说，增大质量以及电容值或者减小弹性系数可提高实现灵敏度。

本文所提出的双轴电容式加速度传感器，通过测量差动电容值实现加速度的检测。当外界加速度a=0时，可动梳齿位于两固定梳齿中间如图2(a)。加速度传感器的电容值为

(3)

式中d0为梳间标称间距;ε0为真空介电常数;ε为相对介电常数;S为梳齿间正对面积。

当加速度a≠0时，质量块受惯性力作用产生位移x如图2(b)，从而引起电容值变化

(4)

(5)

由于x≪d0梳齿位移相对于标称间距很小，对式(4)、式(5)进行泰勒级数展开，可得

(6)

由式(6)可知，加速度传感器的差分电容值与施加的加速度成正比，欲提高其灵敏度可通过提高敏感质量，加大标称电容值，减小电容器间隙及弹性系数实现。

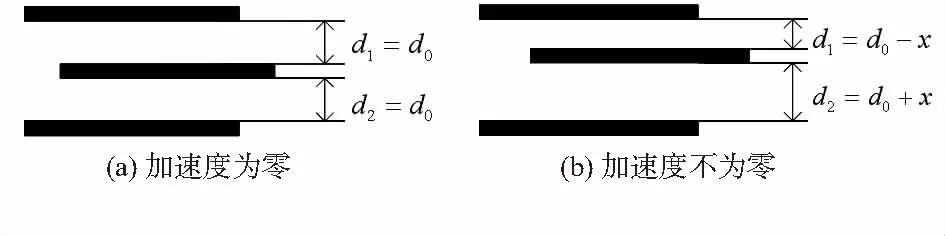
图2 固定梳齿和可动梳齿差动电容值的关系

1.2 结构设计

如图3所示，加速度传感器由两个相互垂直的敏感结构组成，通过弹性悬臂梁连接。内部的敏感质量由四组垂直的折叠梁支撑，而外部的敏感质量则由4组水平的折叠梁支撑，敏感质量的两侧分别有40和21对梳齿。如前所述，当敏感质量受加速度引起的惯性力的影响时，电容器间隙发生改变，因此,可以通过测量差分电容值来实现加速度的检测。

图3 双轴加速度传感器设计结构

图4为U型折叠梁示意，其由两条垂直梁和一个弧形梁组成。U型折叠梁具有工艺简单，低残余应力，弹性系数可调和低跨轴灵敏度等优点。此外，U型折叠梁的固有频率可以随着加速度传感器结构的厚度进行调整，其高阶频率远大于其固有频率，可以有效地降低各模态之间的影响。

图4 U型折叠梁

敏感方向上U型折叠梁的弹性系数可以表示为[8]

(7)

式中L，R，E分别为直梁的长度、弧形的内半径和杨氏模量。Iz为Z轴向的惯性力矩

(8)

式中T为结构厚度。加速度传感器的总弹性系数为

(9)

式中n为U型折叠梁的数量。

加速度传感器的位移灵敏度为

(10)

基于上述公式及ANSYS仿真结果，得优化设计参数如表1。结构厚度为300 μm，电容初始间隙为2 μm。

表1 双轴加速度传感器设计参数

2 结果分析

2.1 灵敏度仿真结果

仿真基于ANSYS进行。为了得到位移灵敏度分别在加速度传感器的X轴向和Y轴向施加1gn的加速度。图5显示了加速度传感器沿着X轴向和Y轴向的位移灵敏度，由图5(a)可知X轴向位移灵敏度为SdX=0.084 511 μm/gn，Y轴向位移灵敏度为SdY=0.138 199 μm/gn。如前所述，由于用了整个厚度的硅片使得加速度传感器具有较大的敏感质量。因此，此结构的位移灵敏度远大于其他参考文献。而SdX

2.2 模态分析

如图6所示为加速度传感器前三阶模态分析结果。谐振频率分别为fX=1 342.25 Hz，fY=1 717.51 Hz和fZ=14 481 Hz。

图5 加速度传感器的位移灵敏度

图6 双轴加速度传感器模态仿真结果

由结果可知第一、二阶谐振频率相近，便于后续检测电路的设计。而且前两阶谐振频率远低于第三阶谐振频率，可以有效降低因跨轴带来的干扰。

3 结束语

提出了一种新型双轴电容式加速度传感器。结构由内、外两个敏感质量组成，分别用于检测X轴向和Y轴向的加速度，可以使输出信号的交叉干扰最小化。通过ANSYS仿真分析得出了传感器的设计参数，并且进行了位移灵敏度和模态的仿真分析。

[1] Aydemir A,Terzioglu Y,Akin T.A new design and a fabrication approach to realize a high performance three axes capacitive MEMS accelerometer [J].Sensors & Actuators A:Physical,2016,244:324-333.

[2] 刘泽良,温银堂,梁 希,等.基于ANSYS的平面电容传感器阵列三维仿真研究[J].传感器与微系统,2016,35(4):45-48.

[3] 姜志国,陈玉玲,史岩峰,等.一种三轴振动传感器设计[J].传感器与微系统,2015,34(5):106-108.

[4] Köse T, Terziolu Y, Azgln K,et al. A single mass two-axis capacitive MEMS accelerometer with force rebalance[C]∥2015 IEEE International Symposium on Inertial Sensors and Systems (ISISS),IEEE,2015:1-4.

[5] Chattaraj D,Swamy K B M,Sen S.Design and analysis of dual axis MEMS accelerometer[C]∥2007 International Workshop on Physics of Semiconductor Devices,2007.

[6] Jayanetti V C,Jayathilaka W A D M,Talawatta K I,et al.Design and simulation of a MEMS-based dual axis capacitive accelero-meter[C]∥Moratuwa Engineering Research Conference,IEEE,2015:194-198.

[7] Serrano-Vázquez F X,Herrera-May A L,Bandala-Sánchez M.Design and modeling of a single-mass biaxial capacitive accelero-meter based on the Summit V process[J].Microsystem Tech-nologies,2013,19(12):1997-2009.

[8] 陈 永,焦继伟,熊 斌,等.一种基于滑膜阻尼效应的新型微机械陀螺[J].中国机械工程,2004,15(2):103-105.