一道高考物理题的典型解法
——2017年高考全国理综卷第21题
2018-01-26 01:31:12王翔
物理通报 2018年2期
王 翔
(武汉外国语学校 湖北 武汉 430022)
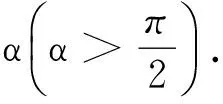
A.MN上的张力逐渐增大
B.MN上的张力先增大后减小
C.OM上的张力逐渐增大
D.OM上的张力先增大后减小

图1 题图
分析:该题属静力学中的动态平衡问题.如图2所示.

图2 受力分析图
取重物(亦可取结点M)为研究对象,它受到竖直向下的重力G;沿MO方向的拉力TOM,大小等于轻绳OM上的张力;沿MN方向上的拉力TMN,大小等于轻绳MN上的张力.此三力共点共面,且构成一个首尾相接的封闭矢量三角形.
解法1:正弦定理

解得

解得
其中α-θ从钝角逐渐减小为锐角,sin (α-θ)先增大后减小,故OM上的张力先增大后减小.
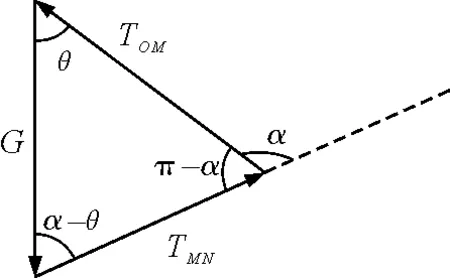
图3 正弦定理分析图
解法2:拉密定理
如图4所示,由拉密定理,可得
解得
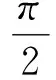
解得
故在α-θ从钝角逐渐减小为锐角的过程中,OM上的张力先增大后减小.
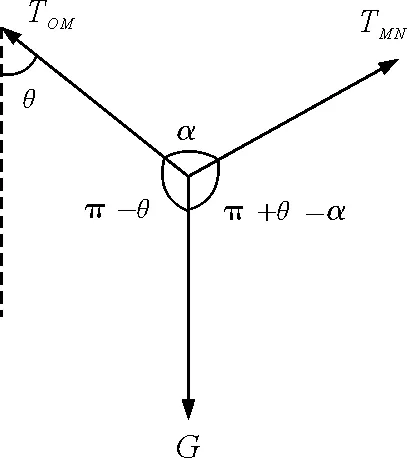
图4 拉密定理分析图
解法3:正交分解
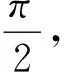
沿x轴方向
解得
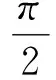
沿y轴方向
代入
得
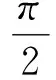
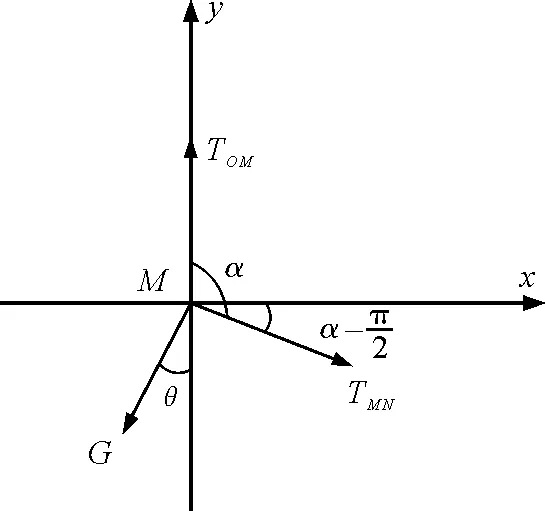
图5 正交分解分析图
解法4:矢量三角形
如图6所示,重力为一恒力且和拉力TOM,TMN构成一封闭矢量三角形,由定弦所对的圆周角相等,可引入以重力矢量为定弦的一个参考圆.如图6所示,OM由竖直被拉到水平的过程中,对应于K点从O1点出发经过P点到Q点的过程,参考圆中直径对应拉力最大,故TMN从零逐渐增大,其最大值对应长度O1Q;TOM从G先增大后减小,其最大值对应长度O2P,最小值对应长度O2Q.

图6 矢量三角形分析图
猜你喜欢
中学生数理化·自主招生(2024年1期)2024-05-29 03:43:56
中学生数理化(高中版.高考理化)(2024年1期)2024-01-27 10:18:38
科学大众(2022年23期)2023-01-30 07:04:16
航空发动机(2020年3期)2020-07-24 09:03:16
新世纪智能(教师)(2019年2期)2019-09-11 05:56:40
发明与创新·中学生(2018年2期)2018-02-07 20:23:21
时代英语·高二(2017年4期)2017-08-11 07:37:57
水利技术监督(2017年3期)2017-06-09 06:55:34
天津体育学院学报(2016年3期)2016-12-18 08:24:54
小天使·一年级语数英综合(2016年9期)2016-05-14 12:21:06

