借助点子图促进“理法”融合
杨凯明

摘 要:点子图这个直观模型是实施数形互化的一种好的抓手。利用点子图,挖掘口算、列表和竖式之间的内在联系,把它们进行有机的融合,为学生的思维搭桥铺路,实现多种算法的意义统一,为后面再研究复杂的笔算模型积累活动经验。
关键词:直观模型;点子图;“理法”融合
中图分类号:G623.5
文献标识码:A
一、思考
在学习北师大版教材三年级上册第四单元《需要多少钱》这一课之前,学生已经学习了两位数乘一位数的算理。本节课是在此基础上学习两、三位数乘一位数的笔算乘法,是三年级上册第六单元的起始课,也是以后进一步学习乘法、除法的基础。
基于以上认识,笔者根据课标的要求,结合学生的学习情况,制订以下学习目标。
(1)在解决问题过程中,引导学生探索并掌握两、三位数乘一位数(不进位)乘法的计算方法,并且能正确进行计算。
(2)利用点子图这一直观的模型,理解笔算乘法每一步的含义,进一步体会算法多样化。
(3)在交流算法的过程中,学会表达自己的想法,逐步养成认真倾听和善于思考的好习惯。
二、实践
1.创设情境,复习算理(回顾两位数乘一位数的口算方法)
(1)出示“蚂蚁做操”的情境图(如图1)。
师:森林运动会举行了,下面是蚂蚁进行的做操表演,我们一起来欣赏。
学生独立观察画面。
师指名回答:谁来说一说这幅蚂蚁做操图中有哪些数学信息?
生1:每行有12只蚂蚁,有4行。
教师板书。
(2)结合数学信息尝试提出乘法问题。
师:你能结合这些数学信息,提出一个数学问题吗?
生2:每行有12只小蚂蚁,有4行,一共有多少只小蚂蚁?(教师板书)
师:这个数学问题该如何列式解答呢?请同学们拿出作业纸,在作业纸上写一写。
教师指名学生回答。
生3:12×4= ?(教师板书)
(3)回顾口算方法。
师:我们已经学过两位数乘一位数的口算方法了,大家回忆一下,有哪些方法和形式?
生4:10×4=40,2×4=8,40+8=48。
师:真不错,这是用横式笔算的方法,还有其他的方法吗?
生5:用列表法。
生6:可用画图法,就是画点子图的方法。
师:大家说得都很好,接下来请同学们在作业纸上用刚才说的方法来计算12×4,要求是:不管是用列表法还是画点子图都要想一想先算什么、再算什么。
(4)学生独立完成,教师巡视,个别指导。教师在作业纸上为学生提供表格和点子图。
(5)全班交流汇报。
师:下面,哪位同学来向大家汇报一下你自己方法?
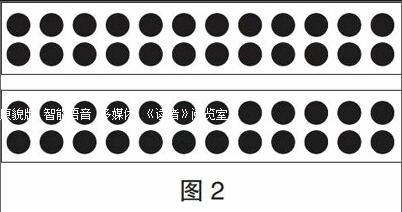
生6:我用的是画点子图,把点子图分成上下两部分,上面这部分每行12个,2行就是12×2=24,下面的也一样,算式24+24=48(如图2)。
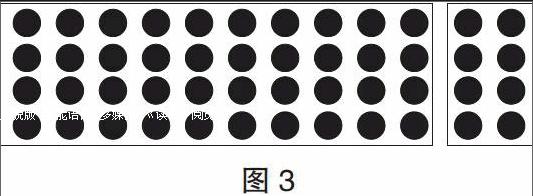
生7:我也是画点子图的,把点子图分成左右两部分,一部分是每行10个,圈这样的4行,10×4=40;另一部分是每行2个,圈这样的4行,2×4=8;再将两部分加起来,40+8=48(如图3)。
师:这两种圈点子图的方法,你们觉得怎么样?
生8:我更喜欢第二种,因为它看上去更容易理解。
生9:我用的是列表法,把12分成10和2,把10和2分别写在表格里,乘号也写在表格里,10×4=40,40写在10下面这一行里,2×4=8,8写在2下面的这行里,最后40+8=48(如图4)。
生10:我觉得圈的方法很多,都可以得到48这个得数。
师:同学们很会思考,今天我们要来学习一种新的计算方法,那就是用竖式计算乘法。
2.探究新知,“理法”融合(探索竖式计算方法,理解竖式每一步的算理)
让学生尝试列竖式计算。大致出现以下两种方法,教师投影展示竖式。
师:这是一位同学列的竖式(如图5方法①),你们知道他是如何列出来的吗?
生1:他是:12乘4,2乘4得8,8写在横线下面,10乘4等于40,40写在8的下面,最后8加40等于48。
生2:我觉得用竖式的方法跟点子图的意思是一样的(指着图3),竖式的第一步2×4=8就是点子图的每行2個、共4行的这一部分,竖式的第二步10×4=40就是点子图的每行10个、共4行的这一部分,然后再加起来。
生3:我觉得它跟列表法的意思也一样的。竖式的第一步2×4=8就是表格第二行中的8,第二步10×4=40就是表格中的40,然后把40和8相加。
师:发言都很精彩,大家再来整理一下刚才他们的发言。竖式中先算2乘4得8,在点子图中就是每行2个、共4行的这一部分,在列表法中就是第二行的8,在横式中就是2×4=8,结果是8,所以要写在个位上。竖式中再算10乘4等于40,在点子图中就是每行10个、共4行的这一部分,在列表法中就是第二行的40,在横式中就是10×4=40,结果是40,写在第二层,注意要数位对齐,4写在十位上,0写在个位上。竖式最后算40+8=48,点子图就是两部分之和,列表法中就是40+8=48。
在师生交流的时候,为促进学生理解,逐步板书,形成教材中的图(如图6),让学生体会竖式和点子图、列表法之间的内在联系。(师生边交流,边板书,边连线)
教学中结合学生的讨论,向学生介绍一般乘法竖式的简写形式。结合点子图引导学生再次理解8为什么写在个位上,表示什么意思;写在十位上的4表示什么。
3.课堂小结,自我提升(回顾总结自己的收获)
提问:这节课令你印象最深刻的是什么?“点子图”“列表法”的算法对乘法竖式计算的掌握有帮助吗?在用竖式计算的时候要注意哪些问题呢?
三、启示
本节课将点子图与竖式计算中的每一步相互对应起来,清晰地呈现出两位数乘一位数的乘法竖式的计算过程,同时还沟通了数据列表、抽象的竖式与直观的点子图三者之间的内在联系,有利于学生理解每一步的具体含义,经历从直观形象到抽象思考的数学化的过程。因此,教师在计算教学中要足够重视点子图的运用,善于挖掘此类素材。
参考文献:
[1]刘安平.活用点子图 妙得新思路[J].学周刊,2016(7).
[2]侯木华.规范使用点子图 把握概念准确性——由“在点子图上画出两个不同平行四边形”引发的争议与思考[J].教育实践与研究(A),2015(10).endprint

