立足教材 延伸课外
秦进 陈明 张少华 代姗妮 简萱慧

基金项目:贵州省科学技术基金项目(黔科合LH字(2015)7042号)。
摘要:教科书是根本,既要重视教材基本知识的普及,又要注重能力的提高,要对教材真正理解。本文从对教材的观点认识、拓展内容和思想延伸等几个方面阐述了教材延伸是十分必要。
关键词:教材;内容;延伸
几何内容是中小学数学课程重要的组成部分,教育部于2001年7月正式颁布了《全日制义务教育阶段数学课程标准》,在《标准》中将几何作为重要的内容列入到我国义务教育各阶段的数学课程。义务教育阶段七至九年级人教版、北师大版、华师大版等教科书中的几何内容比较接近,人教版安排在第四、第五、第六、第七、第十一章等共十三章。教科书中几何内容主要涉及图形的认识初步、平面直角坐标系、勾股定理、投影与视图等。教师应该站在高度来审视教材,根据课程的需求对教材进行分析,特别是对教材深入理解认识,延伸拓展。以知识重构为切入点,体验学习数学内容的过程,运用“高观点”分析和处理中学数学问题,有利于提升教师的专业能力。
一、 观点认识
人教版教科书是按照“简单说理”“说理”“推理”“用符号表示推理”等不同层次,分阶段逐步加深安排的。通过活动认识图形,十分重视学生的动手操作和参与,教育部审定(2013)人教版教科书七年级上第四章图形的初步认识,注重利用实物和几何模型进行教学,采用实物入手,展示多彩的图形世界与几何知识的密切联系,第119页,笔尖可以看作一个点,这个点在纸上运动时形成线,节日的焰火也可以看成有点运动而成的,笔尖作为一个点运动成圆(图1),汽车雨刮器在挡风玻璃上画一个扇面(图2)。点动成线,线动成面的角度进一步认识几何基本图形,几何图形可看成是点的集合点,几何图形也可以理解为由线组成,点和线两者是相互对应的,点为元素的几何观点和线为元素的几何观点是统一的。平面可以看成点为元素的集合,也可以看成直线为元素的集合;圆可以看成由点构成,也可以看成由直线构成,如图3所示,线包络成圆。可以以点为元素来表达几何对象,事实上,我们完全可以以直线为元素来表达几何对象,几何图形看成是直线的集合。
1831年,普吕克在《解析几何论》第二部分所述,将点坐标与线坐标进行类比“对偶”的方法建立解析几何结构,线几何的观点在射影几何中体现十分显著。点和直线的地位是平等!点有方程,直线有坐标。平面可以看成直线为元素组成;锥面是由一簇直线构成;单叶双曲面、抛物双曲面以及柱面等直纹面实质上是由直线运动生成的曲面;二次曲线看作点的轨迹,也可以看作直线的包络。《普通高中数学课程标准(实验)》(苏教版)选修21中“探究·拓展”内容就体现了线几何的观点,引进齐次线坐标,打破了中学解析几何点与数组一一对应的坐标观点,将以点为基本元素的点几何学转化为直线为元素的几何学。平面上的基本元素直线与点,它们之间的关系是结合关系。满足三元二次方程的点集合称为二次曲线(二阶曲线),满足三元二次方程的直线集合称为二次曲线(二曲级线),二次曲线是成射影对应的点列对应点的联线的集合。这样高度概括的认识,抓住事物的本质,体会数学的观点,打开认识的视野。
二、 思想延伸
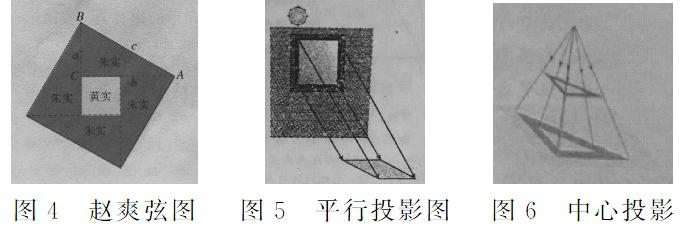
从数学文化的角度来说,培养数学的思想和方法是极为重要的。变与不变的数学思想和方法就是其中之一,可以說它贯穿义务教育阶段教科书的始终。教育部审定(2013)人教版教科书八年级下第十七章勾股定理,赵爽弦图(图4),赵爽根据此图指出:四个全等的直角三角形(红色)可以围成一个大的正方形,中空部分是个小正方形(黄色),通过对图形的切割,拼接,巧妙利用面积关系证明了勾股定理.所谓的“出入相补”原理。此方法严谨而简洁,这种证明的方法被一些数学家称为“最省力的证法”,证明过程显示了图形间的相互关系,特别是体现了变与不变的数学思想。刘徽注《九章算术》时,也给了证明,留下注文:“勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不移动也,合成弦之幂,开方除之,即弦也。”由于刘徽使用的弦图已经失传,后世数学家只能根据这段注文进行多种解释与推测,清代数学家李潢的补图简单明了,接近刘徽之意。“出入相补,各从其类”,这个原理是说一个平面图形从一处移到另一处,面积不变,形状可能发生变化,体现了变与不变的数学思想。纵观勾股定理证明的欧几里得证明、美国总统Garfield证明、辛卜松证明、梅文鼎证明、杨作玫证明、李锐证明等近20种方法都体现了变与不变的数学思想。
几何变换用近代数学的观点来看就是“几何运算”,几何变换把一个几何图形变为另一个几何图形,什么变了?什么没有变?共同的属性是变中有不变!教科书九年级下第二十九章投影,涉及平行投影与中心投影等。阳光透过长方形玻璃窗平行投影到地面上,地面上出现一个明亮的四边形(如图5),我们应该关注这个几何变换中的不变量与不变性质;如图6,此中心投影将三角形变为三角形,形状没有发生变化,三角形还是三角形,但是三角形的角的大小,边的长度可能发生变化了。用变换群去研究相应的几何学,阐述了几何学的本质是变中有不变,既要抓不变量与不变性质的“不变”,又要抓量与性质的“变”。多边形的内角和与边数有关,而多边形的外角和恒等于360度;又如,等底等高的两个三角形面积相等;等腰三角形底边上一点到两腰的距离之和是常数(定值)等等均蕴含变与不变的数学思想。
三、 内容拓展
人教版教科书第二十四章圆安排了探索四点共圆的条件,利用探究过程,归纳出证明四点共圆的方法主要有四种:一是如果四点到一定点的距离相等,那么这四点共圆;二是四边形的一组对角互补,那么这四边形的四个顶点共圆;三是如果四边形的一个外角等于它的内对角,那么这四边形的四个顶点共圆;四是如果两个三角形有公共边,公共边所对的角相等,且在公共边的同侧两个三角形的四个顶点共圆,通过实践探索对教材内容进行拓展。
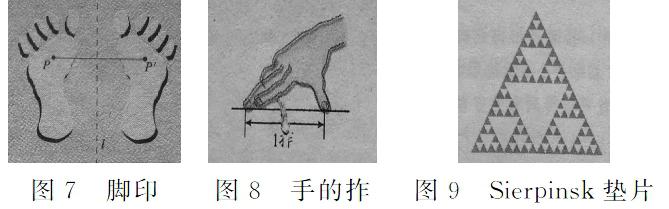
第十三章中的轴对称中的最短路线问题,可以延伸到作图问题,拓展到对称变换、平移变换以及旋转变换等进行理解,体会对应点、对应线段、对应图形之间的关系。如图7,左脚印和右脚印中链接一对对应点的线段被对称轴垂直平分。可以理解为右脚印可以通过左脚印经过对称变换得到的。其中,P点变为P′,这一对应点连线段被l平分。第二十七章相似中涉及长度的测量,测量离不开单位。测量长度的常用工具有游标卡尺、钢卷尺、木尺等,如果测量的精度要求不高,可以用步长、肘、拃(如图8)来测量距离。测量依赖于测量工具,归根结底紧紧依赖于单位!数轴的三要素坐标原点、正方向以及长度单位,单位取得不一样,坐标不一样,直角坐标系亦如此。直角坐标系经过仿射变换后得到新的坐标系——仿射射坐标系的x轴与y轴的单位长度也未必一样。把一个正三角形分为全等的四个小正三角形,去掉中间一个正三角形,对剩下的3个小正三角形再分别重复以上做法……将这种做法继续下去,就能得到小格子越来越多谢尔宾斯基地毯(如图9)。这个图的大大小小的三角形之间关系是相似,局部与整体之间是自相似的关系。
图7脚印图8手的拃图9Sierpinsk垫片
这种现象广泛存在,自然界大多数的图形都是十分复杂而且不规则的。例如,海岸线、树木、闪电、海浪等等,它们在欧氏几何领域不可度量,而分数维恰好反映了这种不规则性和复杂性。从传统的几何学出发,用什么样的尺子都很难测量很复杂的几何对象。从分形几何学出发,我们用一个看起来很复杂的测量单位去测量几何对象,所得的结果却十分简单。
用好教材,必须真正理解教材,把握内容之间的联系,从另外一个视角来审视教材,注重观点认识、拓展内容和思想延伸显得尤为必要。
参考文献:
[1]义务教育教科书.数学(7~9年级)[M].北京:人民教育出版社,2014.
[2]梅向明.高等几何[M].北京:高等教育出版社,1983.
[3]罗崇善.编写国家级重点教材《高等几何》的思考[J].四川师范大学学报(自然科学),2000(11).
[4]朱德祥.高等几何[M].北京:高等教育出版社,1992.
[5]秦进.圆锥曲线的线几何观点认识法[J].中学数学教学参考,2014(11):54-55.
[6]秦进.圆锥曲线的中心射影认识法[J].中学数学教学参考,2014(10):40-41.
[7]秦进.高等几何课程教学的认识与实践[J].遵义师范学院学报,2017(4):108-110.
作者简介:
秦进,陈明,张少华,代姗妮,贵州省遵义市,遵义师范学院;
简萱慧,贵州省遵义市,遵义市第十六中学。

