基于改进蚁群算法在工程项目工期—成本优化问题研究
叶民权 吴佳洁 郑晨虹 喻婧
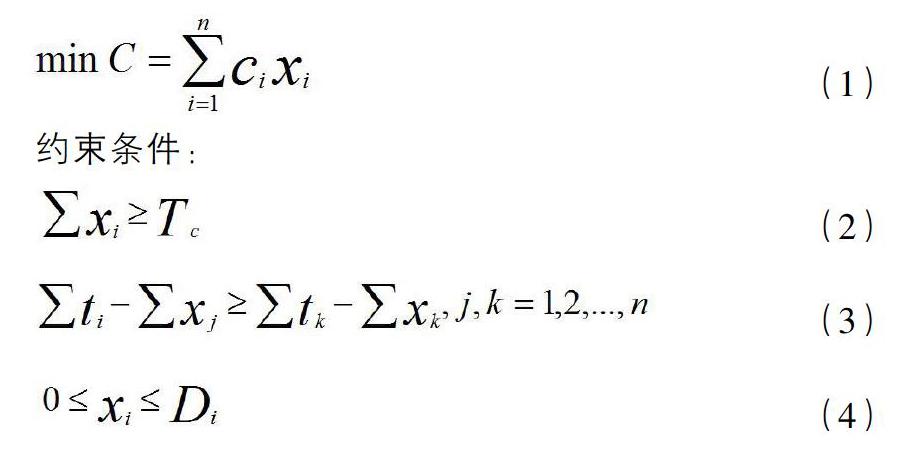


摘要:為了解决蚁群算法容易陷入局部最优,求解容易出现停滞现象,本文从转移概率和信息素挥发因子两方面对蚁群算法进行改进,并将其应用于工程项目工期成本优化问题中。本文将改进后的蚁群算法应用于某变电站土建项目,结果表明改进后的蚁群算法其性能优于基本蚁群算法,解决了算法由于固定参数而导致的停滞问题,在工程项目工期成本优化问题的应用取得了良好的效果。
Abstract: Ant colony optimization (ACO) is easy to fall in local optimum and has slow convergence rate. In order to solve the problem, this paper employs an improved ant colony optimization (IACO) algorithm which is modified in volatile factor as well as transition probability and successfully applies to time-cost optimization in specific example. Comparing with basic ant colony algorithm, this new method increases the ability of global searching and constringency, thus can settle out the stagnation of the process and find the optimum value. The results indicate that the improved ant colony algorithm is effective in time-cost optimization.
关键词:蚁群算法;工程项目;参数改进;工期成本优化
Key words: ant colony algorithm;project;improved parameters;time-cost optimization
中图分类号:TU72;TP18 文献标识码:A 文章编号:1006-4311(2018)34-0087-03
0 引言
工程项目的工期和成本一直以来受到项目管理者的重视,其也直接影响到工程的质量,项目的工期和成本存在相互制约、相互影响的关系。一直以来,工程的工期—成本优化问题一直是优化领域的一个重点研究对象,其要求在特定的约束条件下,保证每个供需能够以最优的方案执行,满足项目管理的需要,确保工程项目顺利完成。
到目前为止,对工期—成本优化问题的求解方法有很多,传统的线性规划方法[1]是一种运用较为成熟的优化方法,具有计算方法简单、求解速度较快优点。但是在实际的应用过程中,其存在计算误差大,精度较低的缺点,也限制了其在实际问题的应用。随着计算机技术以及人工智能技术的不断进步,人工智能优化算法也被广泛运用到项目工期—成本优化问题上,其主要有禁忌搜索法[2](TS)、模拟退火法[3](SA)、粒子群算法[4](PSO)、遗传算法[5](GA)等。这些算法具有较快的求解速度,能够较为高效的完成最优解搜索,在一定程度上较传统优化方法提高了最优解的质量,但是上述方法均存在计算时间过长以及容易陷于局部最优等问题,难以实际应用到项目工期—费用优化问题中。
本文用改进参数的蚁群算法解决项目工期—成本优化问题。以规定工期条件下成本最小作为优化目标,比较得出改进的蚁群算法获得的最优解均优于普通蚁群算法,而且收敛速度也较快。
1 工期—成本优化问题的描述以及数学模型
在工程项目实施过程中,包含n个项目活动。为保证基建项目工期—费用优化问题的解决,先采用PERT网络技术建立优化模型。在该优化模型中,假定在优化过程中关键路线不发生变化。结合工程项目实施过程中的特点,本文以压缩工期确定的条件下成本最小作为优化的目标,其工期—费用优化模型的表达式为:
其中,ci是单位时间内项目活动i的压缩费用,xi是项目活动i的压缩时间,TC是需要压缩的工期,tj和xj分别为闭合圈内关键路线上项目活动i的平均持续时间和压缩时间,tk和xk分别为闭合圈内非关键路线上项目活动的平均持续时间和压缩时间,?啄j是第j个闭合圈内所有项目活动的方差的均方根,?姿j是第j个闭合圈在规定日期内完工的概率,Di是项目活动i的极限压缩时间;式(1)是目标函数,表示基建项目的成本最小;式(2)~(4)是约束函数,表示压缩过程中必须满足的四个约束条件。
2 蚁群算法基本内容及其改进原理
2.1 蚁群算法基本内容
蚁群算法(Ant Colony Optimization,ACO),又称为蚂蚁算法,是由意大利著名学者M.Dorigo于20世纪90年代初提出的一种新的模拟进化算法[6-7]。蚁群算法最初用于解决旅行商问题(TSP),也是最典型的应用问题,即给定n个城市,旅行上需要遍历所有的城市,最终回到出发城市,从而寻找最短的旅行路线;另外,每个城市只能经过一次,但是出发城市可以经过两次。
2.2 蟻群算法的改进
蚁群算法在优化问题求解的过程中经常会遇到收敛速度慢、搜索能力较弱的问题,为了解决上述缺陷,本文从信息挥发因子和转移概率两个方面进行优化,确保蚁群算法的求解能力[8]。
2.2.1 挥发因子的改进
蚁群算法的全局搜索能力和收敛速度的大小,其挥发因子?籽具有相当重要的地位,本文针对蚁群算法挥发因子的不足与缺点,创新的提出一种可以随时间调整挥发因子值的大小的优化方法,目的是及时调整各个时间段参数的适应能力,保证蚁群算法的求解能力。其具体做法如下:
籽的初始值?籽(t0)=1,当蚁群算法求得的最优值在N次循环后没有明显改进时,?籽按照以下公式进行调整:
式中,?籽min为?籽的最小值,从根本上防止?籽过小而导致算法的搜索速度减慢的现象发生,一般设定?籽min=0.1。每次求解完成后,对本次的最优解进行储存,提高了算法的搜索能力。
2.2.2 转移概率的改进
蚁群算法的求解速度和精度的大小,其参数?琢与?茁在发挥着不可或缺的作用,其决定了状态转移概率的大小。目前为止,二者的取值一般根据经验设定,没有较为科学的取值方法。为了解决以上问题,本文提出了以下的方法对两参数进行设置:
其中,Nmax为最大迭代次数,公式(10)将参数?琢与Nmax相互关联,随着Nmax的变化而变化;公式(11)则体现了参数?茁通过参数?琢的取值来决定,二者也是相互关联的。依据上述公式,可以直观的看出参数?琢与?茁的取值与Nmax进行关联,保证了算法各个参数之间的联动,减弱算法参数设置的随机性。
3 实例分析
本文按照变电站土建项目的特点,以变电站土建部分为研究对象,进行变电站的工期—费用优化问题的研究。图1为该变电站的PERT网络图,表1为各个工序的相关参数。依据该项目的施工组织设计,其计划总工期为582天,而业主单位在542天内完成土建建设部分。
在算法参数设置方面,对算法中各个参数初始化,首先设定最大迭代次数Nmax,由此得到相应的参数?琢、?茁;设定蚂蚁数量m=28;最小挥发系数?籽=0.1;Q=1。由于Nmax的大小直接与参数?琢、?茁的大小相关,也将影响算法的求解能力,本文设定了不同的迭代次数,从而获取不同的优化结果。其优化结果如表2所示。
从表2可以直观的看出,当Nmax=80时,改进后的蚁群算法取得了最优值,此时的迭代次数为12次,具有较快的收敛速度,一定程度上避免了算法的早熟。因此本文取Nmax=80时进行改进蚁群算法的比较,其算法比较如图2所示。
图2所示为改进后的蚁群算法与未改进的蚁群算法寻优结果的比较,虚线为改进后蚁群算法,实线为未改进蚁群算法。Nmax=80时得到最优压缩天数为x={5,0,0,0,0,0,2,3,14,0,0,0,0,5,0,0,0,0,0,6,5,5},压缩后最优工期为d={25,45,61,123,72,154,38,88,129,123,92,76,105,19,
123,92,72,91,31,30,27,25},压缩调试后该项目的总工期T=542,压缩费用为C=250710元。
从图中可以明显看出改进蚁群算法的寻优结果优于未改进的蚁群算法,其主要表现在两方面:①改进的蚁群算法得到的最优值明显优于未改进蚁群算法的最优值,改进算法得到的最小压缩成本为250710元,而蚁群算法得到的压缩成本为268790元;②改进蚁群算法摆脱了蚁群算法早熟,易陷入局部最优解的缺点。图中蚁群算法在迭代次数为7时得到本次迭代的最优解,算法明显早熟,而改进蚁群算法在12次时算法才得到最优解,避免了算法的早熟。因此,改进参数后的蚁群算法对项目工期成本优化问题有更好的应用。
4 结论
工程项目的工期—成本优化问题一直以来都受到项目管理单位的重视,其优化问题在学术领域也是一个难点和重点。为了解决蚁群算法搜索速度较慢,搜索能力较弱的缺陷,本文提出了自适应调整信息素挥发因子和状态转移概率参数的改进方法,增强算法的适时调整能力,有效地将算法参数联动。通过变电站土建工程案例分析,可以直观的看到,改进后的蚁群算法相比传统的蚁群算法能够较快的得到最优解,并且该最优解为全局最优,保证了算法的求解能力,避免了局部最优和早熟的问题。结果表明,改进后的蚁群算法在工程项目工期成本优化问题中具有一定的推广性。
参考文献:
[1]Liu L,Bruns S A,Feng C W.Construction time-cost trade-off analysis using LP–IP hybrid method[J].Journal of Construction Engineering and Management, 1995,121(4):446-454.
[2]Peng, JN, Sun, YZ, Wang, HF. Optimal PMU placement for full network observability using Tabu search algorithm[J], INTERNATIONAL JOURNAL OF ELECTRICAL POWER & ENERGY SYSTEMS,2006,5:223-231.
[3]Bandyopadhyay, S, Saha,S, Maulik,U, Deb,K. A simulated annealing-based multi-objective optimization algorithm: AMOSA [J]. IEEE TRANSACTIONS ON EVOLUTIONARY COMPUTATION,2008:269-283.
[4]Del Valle Y, Venayagamoorthy G K, Mohagheghi S, et al. Particle swarm optimization: basic concepts, variants and applications in power systems[J]. Evolutionary Computation, IEEE Transactions on, 12(2), 2008:171-195.
[5]Santosh Mungle ,Lyes Benyoucef,Young-JunSon,M.K.Tiwari.A fuzzy clustering-based genetical agorithm approach for time–cost quality trade-off problems:A case study of highway construction project[J].Engineering Applications of Artificial Intelligence 26 (2013)1953-1966.
[6]熊鹰,匡亚萍.施工项目工期与成本优化问题的蚁群算法[J].浙江大学学报,2007,41(1):177-180.
[7]熊鹰,匡亚萍.基于蚁群算法的施工项目工期-成本优化[J].系统工程理论与实践,2007,3:105-111.
[8]马天男.城市配电网网架优化研究[D].华北电力大学(保定),2014.

