求解二维粒子输运方程的CGS算法
张慧慧
摘要:本文采用CGS算法来求解二维粒子输运方程。首先通过离散纵标法将输运方程离散为线性方程组的形式,同时引进预条件矩阵来改善系数矩阵的谱性质。通过数值试验,将预处理后的CGS算法与传统的源迭代方法进行对比,并对預处理前后特征值的分布做了比较。结果表明预处理后的矩阵特征值分布较为集中,且CGS算法收敛速度较快。
Abstract: In this paper, CGS algorithm is used to solve two-dimensional particle transport equation. First, the dispersion equation is used to discretize the transport equation in the form of a linear system of equations. At the same time, the preconditioned matrix is introduced to improve the spectral properties of the coefficient matrix. Through numerical experiments, the preprocessed CGS algorithm is compared with the traditional source iterative method, and the distribution of eigenvalues before and after pretreatment is compared. The results show that the distribution of matrix eigenvalues after preprocessing is more concentrated and the CGS algorithm converges faster.
关键词:输运方程;GGS算法;预条件子;源迭代
Key words: transport equation;CGS algorithm;preconditioner;source iteration
中图分类号:TP301.6 文献标识码:A 文章编号:1006-4311(2018)03-0169-03
0 引言
粒子输运方程是一类重要的偏微分方程,它所描述的是微观粒子输运过程。由于微观带电粒子在输运过程中与物质发生的各种复杂的相互作用,所涉及的是多尺度强非线性复杂系统,导致强耦合的高度非线性问题,所以对粒子输运方程我们采用数值方法求解。
求解输运方程源迭代方法是最常用的一种方法,但此方法只适用于那些系统相对简单的输运方程,对于系统相对复杂的方程,该方法便不适用。因此本文采用CGS算法来求解粒子输运方程。通常用CGS算法来求解方程时,其迭代收敛的速度都与系数矩阵的谱性质有密切联系,因此改善系数矩阵的谱性质变得十分重要。预条件算子就是一个可以很好的实现这一转换的矩阵。目前构造预条件的方法有很多,在本文中构造了矩阵近似逆预条件矩阵和基于高斯分裂的预条件矩阵。最后通过数值试验对预处理前后的系数矩阵的特征值分布进行分析,并且对预条件的CGS算法和源迭代方法求解输运方程的收敛快慢进行了比较。
1 粒子输运方程及其离散方法
1.1 二维粒子输运方程基本理论[1-2]
3.2 预条件矩阵的构造
所谓预条件技术就是将线性方程组Ax=b变成与之同解的线性方程组M-1Ax=M-1b,这里为预条件矩阵。构造一个好的预条件矩阵是非常重要的,既不能增加计算量,又需要尽可能使预处理后的矩阵M-1A的特征值分布在某一点的附近。目前,预条件矩阵的构造方法有很多,本文将构造两种预条件矩阵。
第一种是近似逆预条件矩阵,其思想是构造与系数矩阵的逆矩阵近似的矩阵M。这里,将系数矩阵A的逆展开,即:
第二种预条件矩阵的构造是取线性稳定迭代法中相应的A的分裂。本文中通过高斯分裂得到预条件矩阵,首先将系数矩阵分裂为A=D-L-U,其中D是对角矩阵,L和U分别为A的严格下三角和严格上三角矩阵,于是得到第二种预条件矩阵基于高斯分裂的预条件矩阵[5]:M2=(D-L)-1。
4 数值实验
在本文的数值实验中给出的停机标准是相对残差范数之比满足:
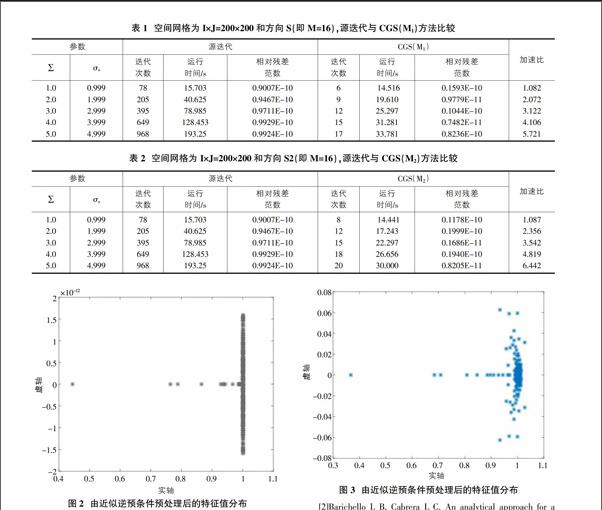
首先通过图1、图2、图3对系数矩阵预处理前后的谱分布进行分析,图1是原系数矩阵的谱分布图,图2、图3分别是由近似逆预条件矩阵、基于高斯分裂的预条件矩阵预处理后的谱分布图。从三个图中我们可以发现经过预处理后的系数矩阵特征值集中分布在1附近。
下面给出的是数值实验结果。表1给出的是空间离散网格为I×J=200×200和方向离散为S2(即M=16)时,源迭代与近似逆预条件的CGS方法的比较。表2将给出空间离散网格为I×J=200×200和方向离散为S2(即M=16)时,源迭代与基于高斯分裂预条件的CGS方法的比较。
从以上两个表格中我们可以得到,对于系统相对简单的输运方程,源迭代方法还是很实用的。但是对于相对复杂的系统,预条件的CGS算法收敛所需的迭代次数和CPU时间都比源迭代要少很多,同时还可以发现随着∑和σs的同步增大,每种迭代方法各自收敛所需的迭代次数和CPU时间都随之增大。对比两种预条件矩阵对加速CGS算法收敛效果,可以得出近似逆预条件的CGS方法收敛所需的迭代次数略少一些,基于高斯分裂预条件的CGS方法收敛所需的CPU时间要快一些。
5 结论
CGS算法是求解大型非对称线性方程组的一种常见方法,本文将该算法与预条件技术相结合来求解二维粒子输运方程,并且与源迭代方法进行比较。数值试验表明预条件技术有效的改善了系数矩阵的谱性质,从而加快了CGS算法的迭代收敛速度。endprint
参考文献:
[1]Mazumdar T, Degweker S B. Solution of neutron transport equation by Method of Characteristics [J]. Annals of Nuclear Energy, 2015, 77(5):522-535.
[2]Barichello L B, Cabrera L C. An analytical approach for a nodal scheme of two-dimensional neutron transport problems [J]. Annals of Nuclear Energy, 2011, 38(6):1310-1317.
[3]杨波.离散纵标法求解含有各向异性散射的输运方程[D]. 中国工程物理研究院,2005.
[4]Kashi S, Minuchehr A, Zolfaghari A, et al. Mesh-free method for numerical solution of the multi-group discrete ordinate neutron transport equation [J]. Annals of Nuclear Energy, 2017, 106:51-63.
[5]張兰.稀疏矩阵方程组预处理迭代技术研究[D].华南理工大学,2010.
[6]Gene H.Golub. 矩阵计算(英文版)[M].人民邮电出版社,2009.
[7]张建华,戴华.求解具有多个右端项线性方程组的总体CGS算法[J].高等学校计算数学学报,2008,30(4):390-399.
[8]Zhao Z Y, Zhang Q M, Tan G L, et al. A new preconditioner for CGS iteration in solving large sparse nonsymmetric linear equations in semiconductor device simulation[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2006, 10(11):1432-1440.endprint

