单圈图的边优美性

陈淑贞, 薛茗曦

(海南师范大学 数学与统计学院，海南 海口 571158)

图标号问题由Ringel G和Rosa A在上世纪60年代中期提出并引起国内外许多学者的关注[1,2]，已成为图论中一个重要而活跃的研究分支.从图的优美标号被提出到现在已有三十来种图标号被定义[3].单圈图(只含一个圈的图)是一类重要的图形. 1984年，Truszczynski M关于单圈图的猜想: 除Cn(n≡1,2(mod 4))外，所有的单圈图都是优美的[4]. 从那时起，关于单圈图的研究一直未间断过，至今已有许多研究成果[3-8].1985年，Lo S引入边优美图的概念[9]，并给出边优美图的必要条件. 对图的边优美性的研究虽然已取得一些研究成果,但仍有许多问题尚待解决. 关于单圈图的边优美性有一个重要猜想[5]：奇阶单圈图是边优美的.本文研究了奇阶单圈图的边优美性问题，给出三类奇阶单圈图的边优美标号.

1 相关定义

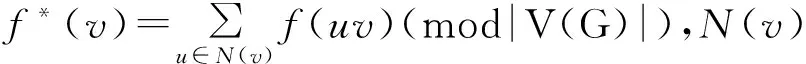
以下所定义和研究的图均为简单图.

定义2 在回路Cm相邻的两个顶点处分别粘接一条路所组成的单圈图称为靶图,记为Ω1(m,2).

定义3 在回路Cm相距为2的两个顶点处分别粘接一条路所组成的单圈图称为定靶图,记为Ω2(m,2).

定义4 在回路Cm的一个顶点处粘接两条路所组成的单圈图称为风筝图,记为Ω(m,2).

2 主要结果

定理1 奇阶靶图Ω1(m,2)是边优美图.

证明设Ω1(m,2)的顶点数为2n+1(n>1)个，其中圈中有m个点，且有

|V(Ω1)|= |E(Ω1)|= 2n+1,

如图1所示，靶图Ω1(m,2)的顶点依次记为a1,a2,…，ai,…，a2n+1.定义其边标号f如下：

f(akak+1)=k(k=1,2,…，2n),f(ai+1ai+m)=2n+1.

显然，边标号f是E(Ω1)到{1,2,3,…,2n+1}的双射.

由f导出的点标号f*为：

f*(ak)=k-1+k=2k-1(k=1,2,…,n)，f*(an+k)=[2n+2k-1](mod|V(Ω1)|)=2k-2(k=1,2,…，n+1).

特别地，顶点ai+1和ai+m有三条相关联的边，但多出的边ai+1ai+m满足

f(ai+1ai+m)=2n+1,

以上计算结果仍然成立.

显然，f的导出映射f*是V(Ω1)到{0,1,2,…,2n}双射,所以靶图Ω1(m,2)是边优美图.图2给出了靶图Ω1(m,2)的边优美标号.

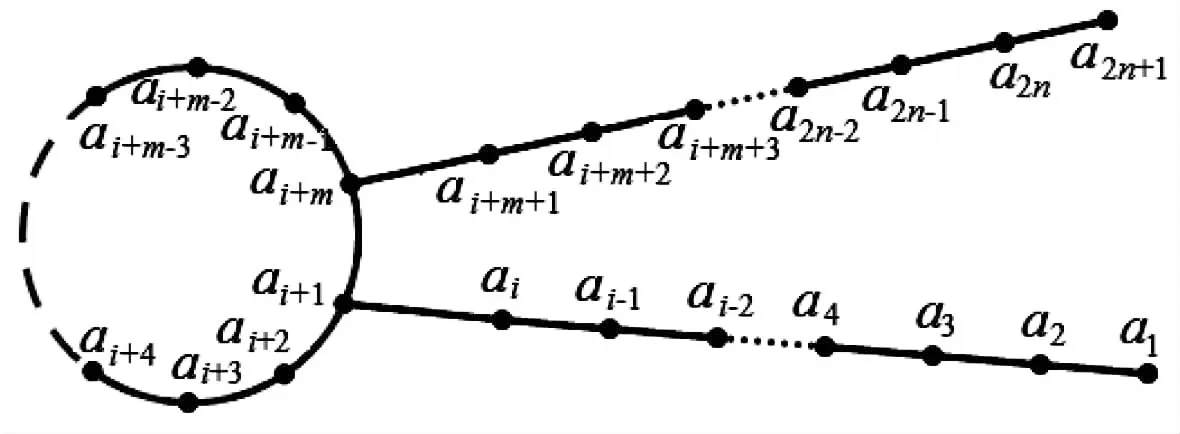
图1 奇阶图Ω1(m,2)Fig. 1 The odd degree graph Ω1(m,2)

图2 奇阶图Ω1(m,2)的边优美标号Fig.2 The edge-graceful labeling of odd degree graph Ω1(m,2)

定理2 当回路上的点为偶数，且两条路的长度相差为1时，奇阶定靶图Ω2(m,2)是边优美图.

证明设Ω2(m,2)的顶点数为2n+1(n>3)个，且有|V(Ω2)|= |E(Ω2)|= 2n+1.如图3所示，定靶图Ω2(m,2)的顶点依次记为a1,a2,…，ai,…，a2n+1，其中两条路的长分别为i+1和i,回路中的点数m为2n-2i.定义其边标号f如下：

f(akak+1)=k(k=1,2,…,2i+3,2i+5,…,2n)，f(ai+2a2i+5)=2i+4，f(a2n+1ai+4)=2n+1.

显然，边标号f是E(Ω2)到{1,2,3,…,2n+1}的双射.

由f导出的点标号f*在取模|V(Ω2)|前为：

f*(ak)=2k-1(k=1,2,…，i+1),f*(ai+2)=4i+7,f*(a2i+4)=2i+3,
f*(ai+k)=2i+2k-1(k=3,4,5,…,i+3,i+5,…,2n+1-i).

这2n+1个数恰好取遍集合{1,3,5,…,2i+1,2i+3, …,4i+5,4i+7,4i+9, …,4n-3,4n-1,4n+1}中的2n+1个数，显然取模|V(Ω2)|后点标号一一对应于{0,1,2,…,2n}. 所以f的导出映射f*是V(Ω2)到{0,1,2,…,2n}双射,于是定靶图Ω2(m,2)为边优美图.图4给出了定靶图Ω2(m,2)的边优美标号.

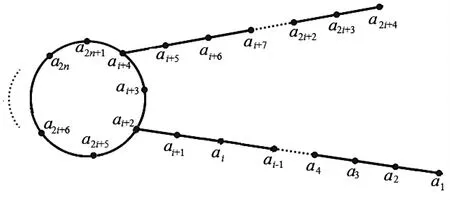
图3 奇阶图Ω2(m,2)Fig.3 The odd degree graph Ω2(m,2)

图4 奇阶图Ω2(m,2)的边优美标号Fig.4 The edge-graceful labeling of odd degree graph Ω2(m,2)

定理3 一条路为n的2n+1阶风筝图Ω(m,2)是边优美图.

证明Ω(m,2)的顶点数为2n+1(n>1)个，则有|V(Ω)|= |E(Ω)|= 2n+1.如图5所示，风筝图的顶点依次记为a1,a2,…，ai,…，a2n+1.定义其边标号f如下：

f(akak+1)=k(k=1,2,…，n-1),f(akak+1)=k+1(k=n+1,n+2,…，2n),
f(anan+m)=n,
f(an+1an+m)=n+1.

显然,边标号f是E(Ω)到{1,2,3,…,2n+1}的双射.

由f导出的点标号f*为：

f*(ak)=2k-1(k=1,2,…n),
f*(a2n+1)=2n+1(mod|V(Ω)|)=0,
f*(an+k)=[2n+2k+1](mod|V(Ω)|)=2k(k=1,2,…,n).

特别地，顶点an+m有四条相关联的边，但多出的边an+1an+m和anan+m满足

f(an+1an+m)+f(anan+m)=2n+1,

以上计算结果仍然成立.

显然，f的导出映射f*是V(Ω)到{0,1,2,…,2n}双射.于是风筝图Ω(m,2)是边优美图. 图6给出了风筝图Ω(m,2)的边优美标号.

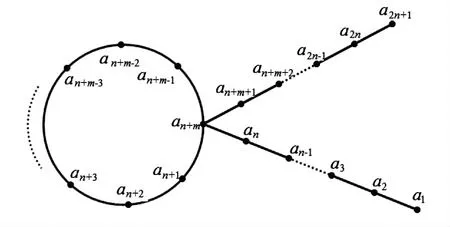
图5 奇阶图 Ω(m,2)Fig.5 The odd degree graph Ω(m,2)

图6 奇阶图Ω(m,2)的边优美标号Fig.6 The edge-graceful labeling of odd degree graph Ω(m,2)

[1] Ringel G. Problem 25 in theory of graphs and its application[C]// Proceedings of the Symposium Smolenice，1963. Prague Publ: House of Czcchoslovak Academy of Science, 1964.

[2] Rosa A. On certain valuations of the vertices of a graph[C]// Theory of Graphs International Symposium, Rome, 1966. Newyork and Dunod Paris: Gordon and Breach, 1967: 349-355.

[3]Gallian J A. A dynamic survey of graph labeling[J]. The Electronic Journal of Combinatorics, 2016, Dynamic Surveys 6: 1-408.

[4]Truszczynski M. Graceful unicycle graphs[J]. Demonstration Math, 1984, 17: 377-387.

[5]康庆德. 图标号问题[J]. 河北师范学院学报，1991(1):102-115.

[7]陈淑贞, 王丽娜. Ω(2, k, n)型图的优美性[J]. 海南师范大学学报(自然科学版), 2008, 21(3)： 249-253.

[8]郑学谦. 图Cn×K2的边优美标号的研究[J]. 太原师范学院学报，2012,11(4):12-13.

[9]Lo S. On edge-graceful labelings of graphs[J]. Congressus Numerantium, 1985(50): 231-241.