有效指导分析策略 提升问题解决能力

级康莉 郭晓倩

中图分类号：G623.5     文献标识码：B    文章编号：1672-1578（2018）31-0134-02

“问题是数学的心脏，解决问题是数学学习的核心”。数学教学不仅是为了让学生学到数学知识，更重要的是把数学应用于现实生活，能够主动从数学的角度分析并解决生活中的实际问题。

省课题《基于问题解决能力提升的小学数学分析策略研究》侧重于对学生解决问题分析策略的指导，使学生掌握必要的方法和策略，从而提升学生问题解决的能力。

1.“画图法”分析策略

画图是解决问题策略中最基本、最重要的分析策略。它不是把现成的图画好呈现给学生看，也不是直接告知怎样画，而是让学生在思考的过程中产生画图的需要，在自己画图的过程中体会方法，感悟策略，发展思维，获得思想。因此，画图是帮助学生解决问题最有效、最常用的方法。

例如：一年级常见的问题，小朋友们站一队，从左数聪聪站在第8个，从右数聪聪站在第7个，这一队一共有多少人？

对于刚接触解决问题的学生来说，他们往往仅凭感觉会把两个数直接相加，8+7=15（人），这样聪聪就被误算了两次。教学中我们可以提醒学生用画图的方法来思考。

如果用“△”代表聪聪，用“○”代表其他小朋友。画图为：

○○○○○○○△○○○○○○

从图中，学生可以很清楚地看出聪聪从左、从右共数了2次，正确列式为：8+7-1=14（人）;同时学生也发现了另一种方法：聪聪左边的人数+聪聪+聪聪右边的人数=总人数，即7+1+6=14（人）

鼓励学生运用画图的方法分析和解决问题，让一些看似复杂的问题，通过画图变得清晰、直观，从而帮助学生分析数量关系，理清思路，促进学生问题解决能力的成长。

2.“假设法”分析策略

假设法是根据问题的已知条件，先做一个假设，然后根据题意和假设之间的矛盾进行分析、调整，寻求解题途径。它是解决“鸡兔同笼”、行程、工程、推理等问题最基本的方法，有利于培养学生的逻辑思维能力。

例如：学校举行知识竞赛，每答对一题得10分，答错一题扣6分，一号选手共抢答8道题，最后得分64分，他答对多少道题？

根据题意，答对一题得10分，答错一题不仅得不到10分，还要扣去6分，即失去10+6=16分。现在假设一号选手8道题都答对了，他应得10×8=80（分），而实际上他只得了64分，失去80-64=16（分）。16÷16=1（题），由此可知，一號选手答错了1道题，答对了7道题。

假设法是一种常用的推测性数学方法，其策略的呈现形式是多样化的。我们应注重引导学生大胆假设，小心求证，把复杂的问题简单化，以达到解决问题的目的。

3.“枚举法”分析策略

枚举法是根据问题本身的性质，一一列举出该问题所有可能的解并在逐一列举的过程中，检查每种可能的解是否正确。该方法在小学数学中应用非常广泛，它能帮助学生整理和筛选有用信息，进行有序思考，从而使问题得到解决。因其逐个考察了所有可能性，所以得出的结论是可靠的。

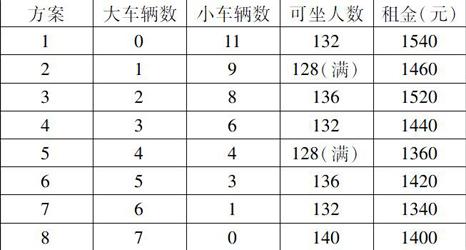
例如：128人外出考察，有两种车可供租用。大车限坐20人，每辆车租金200元;小车限坐12人，每辆车租金140元。怎样租车省钱？

学生一般会认为“坐满没有空位”是最优方案。列举所有情况后发现方案7虽然有空位，却是最便宜的。

方案大车辆数小车辆数可坐人数租金（元）10111321540219128（满）146032813615204361321440544128（满）136065313614207611321340870140

1400  列举全部方案是有必要的，正好坐满的方案，不一定是最优方案。枚举法能够引导学生全面、有序思考，不失为一种有效的解决问题策略。

4.“化繁为简”分析策略

化繁为简就是抛去繁杂的外衣，把问题简化到最原始而又不失其本真的地方。将复杂问题简单化是我们解决问题的一个重要策略。如人教版四年级下册《鸡兔同笼》就是运用了“化繁为简”的思想。

原题为：“笼子里有若干只鸡和兔。从上面数，有35个头，从下面数有94只脚。鸡和兔各有几只？”由于数据较大，经过几次简单猜测和数据调整，学生仍然不能得到正确结果。为了便于研究，可以先从简单的问题入手，把题中的35个头和94只脚改为8个头和26只脚。”

化繁为简可以把复杂问题简单化，学生研究起来更方便，更有利于发现规律，这样可以有效地降低学习难度，提高学习效率。

5.“转化”分析策略

“转化”的分析策略是一种重要的解决问题方法，它把未学过的题目转化成已学过的题目;把繁难的题目转化成简单的题目;把抽象的题目转化为具体的题目，教学中需要我们引导学生灵活运用转化策略化生为熟，化繁为简，化抽象为具体，提高学生问题解决的能力。

在探究图形面积和体积计算公式的推导过程中，都是将所研究的图形转化为已学过的图形。例如：把平行四边形转化

成长方形，把三角形和梯形转化成平行四边形，把圆转化成近似的长方形，把圆柱的体积转化为近似的长方体的体积等，这些都是运用了“转化”的策略。

生活中也有很多需要用“转化”策略解决的问题。比如用排水法测量不规则物体的体积，就是将不规则物体转化为规则物体。以测量土豆体积为例：在量杯中倒入200毫升的水，然后将土豆完全浸没在水中，测出水和土豆的总体积为450毫升，最后用总体积-水的体积=土豆的体积。

在解决实际问题时，要结合具体情境，有意识地培养学生“转化”的分析策略，提高数学思维能力。

总之，在教学中要注重解决问题分析策略的指导，开阔学生的视野，形成多样化的问题解决策略，不断丰富解决问题的方法，使学生的数学思维更具逻辑性、灵活性，最终提升学生问题解决的能力。