计及阀门流量特性的再热凝汽式汽轮机模型及其仿真校验
陈彦峰
(国网湖南省电力公司电力科学研究院,湖南长沙410007)
汽轮机及其调节系统参数实测工作是电网稳定计算的基础性试验项目,汽轮机及其调速系统模型的完善程度是影响电力系统稳定分析可靠性和精确性的重要因素〔1-5〕。近年来,有关汽轮机及其调速系统的建模研究工作已取得了一定成果:文献〔6〕论述了汽轮机所采用的调速控制方式和参数对电力系统稳定计算的影响;文献 〔7〕给出了计及回热器蓄热效应的汽轮机动态模型;文献 〔8〕给出了考虑到高压缸功率过调效应的再热凝汽式汽轮机数学模型。其中部分成果已被一些电力系统专用计算程序 (如电力系统综合分析程序PSASP,PSD-BPA)引用。
常用电力系统专用计算程序中的汽轮机调速器模型一般不考虑机组实际阀门流量特性的影响,或者认为汽轮机阀门流量函数能够准确反映实际的阀门流量特性。然而工程应用中,存在汽轮机阀门流量特性曲线与机组实际阀门流量特性不匹配的情况,通常是由阀门的制造、组装、检修或更换所引起的〔9〕。反映到汽轮机调速器模型上,会使仿真计算的结果与实际现场记录存在差异,进而影响建模精度。所以在建模过程中考虑实际汽轮机调节阀门流量特性的影响以建立精确的汽轮机及其调节系统模型,使其能够用于电力系统稳定分析。
1 再热汽轮机模型及其结构分析
1.1 再热汽轮机数学模型
以电力系统综合分析程序 (PSASP 6.26)为例,其内置的4型调速器模型由3个子模型组成:电液调节系统、电液伺服机构、汽轮机模型。其中电液调节系统模型如图1所示。

图1 电液调节系统模型
该模型包括3种控制模式:调节级压力控制方式、阀控方式、功率控制方式。调速器模型中的电液调节系统的作用是运算生成用于控制伺服机构的阀位指令。伺服机构模型如图2所示。

图2 电液伺服机构模型
电液伺服机构根据阀位指令值形成实际的阀门开度。当主汽压力不变时,阀门开度对应着一定的蒸汽流量。蒸汽进入汽轮机的高、中、低压缸后膨胀做功最终输出汽轮机总体机械功率。汽轮机模型如图3所示。

图3 再热汽轮机模型
图3中,TCH是高压蒸汽容积时间常数;TRH是再热蒸汽容积时间常数;TCO是连通管容积时间常数;FHP为高压缸功率系数;FIP为中压缸功率系数; FLP为低压缸功率系数; FHP+FIP+FLP=1。
1.2 阀门流量特性对汽轮机模型结构的影响分析
通常情况下,汽轮机并网后中调门保持全开状态,此时汽轮机的电液伺服机构指的是高压缸调节汽门 (高调门)。而汽轮机的高调门通常有4或6个,根据 《同步发电机原动机及其调节系统参数实测与建模导则》,当高调门动作特性基本一致时,单个电液伺服机构可以模拟多个高调门。
由于汽轮机调门-蒸汽流量是非线性关系,所以实际的电液调节系统并不会直接形成阀位指令,而是通过阀门流量特性函数对流量指令进行转换,从而形成与之对应的阀位指令。因此,实际电液调节系统如图4所示。

图4 实际电液调节系统
由图4可知,电液调节系统的流量指令经阀门流量特性函数折算成阀位指令,伺服机构根据阀位指令动作形成调门的实际开度。主汽压力不变,汽轮机调门的开度对应一定的蒸汽流量。因此只有当阀门流量函数能够真实反映汽轮机实际阀门流量特性时,则可以不考虑调门指令和蒸汽流量的非线性关系,即可认为调门开度与蒸汽流量是线性对应关系。此时用再热汽轮机模型模拟并网汽轮机组是合适的。而实际上由于调节阀门的制造、安装、更换等因素都有可能使阀门的实际特性与阀门流量函数存在偏差。这时就必须在电力系统稳定计算中考虑阀门流量特性对再热汽轮机模型的影响。
2 计及阀门流量特性的再热汽轮机数学模型及其仿真校验
对某火电厂再热汽轮机组进行一次调频试验。在协调控制方式下,人为地模拟汽轮机转速阶跃变化,快速改变汽轮机出力,从而考察该机组的频率响应特性。该机组的协调控制是基于锅炉跟随方式的,因此当主汽压力在一定范围内变化时,可以不考虑主汽压力的影响,则该机组协调控制逻辑如图5所示。

图5 协调控制系统逻辑框图
图5中的协调控制系统采用前馈—反馈控制。该控制系统功率给定值为原始设定值与一次调频目标值之和。其PID控制器的输出经速率限制环节(变化率限值为30 MW/min)后与一次调频前馈量之和形成流量指令。一次调频目标值和前馈量由DEH转速信号经过转速不等率函数生成,分别叠加至协调控制系统前馈与反馈设定值上。作为PID控制器反馈量的功率信号通过一阶惯性环节以减小和抑制信号波动对机组控制的不利影响。

图6一次调频试验曲线
该机组一次调频试验现场录波如图6所示,当机组模拟转速阶跃改变后,根据转速变化的DEH一次调频功率调整值相应改变,从而使流量指令阶跃增加。协调控制系统CCS中的一次调频功能使其功率给定值增加。在汽机主控调节器的作用下,流量指令随功率给定值与实际功率的偏差相应改变。40 s后,功率曲线基本不再变化,机组处于平衡状态。由于DEH一次调频功能的功率调整值是协调控制系统的前馈信号,且功率前馈系数为1,当机组阀门流量函数能够反映实际阀门流量特性时,则初始流量指令改变量将等于稳态流量指令改变量。而图6中初始流量指令改变量/稳态流量指令改变量约为1.2,如果再考虑到试验过程中主汽压力有所降低,则初始改变量与稳态改变量的比值将更大。所以有必要在该再热汽轮机组建模过程中考虑阀门流量特性的影响。
2.1 计及阀门流量特性的再热汽轮机模型
建立考虑阀门流量特性的再热汽轮机模型,模型假设流量指令等效于阀位指令,即阀门流量特性函数f(x)=x。而实际阀位-蒸汽流量特性为非线性关系,对实际阀门流量特性进行线性化处理,将其简化为一分段线性函数,即假设阀门与蒸汽流量呈线性关系,只是在不同的工况下,斜率不同。
在使用改进模型之前,需根据工况点确定分段线性函数的斜率K。利用图6中一次调频试验数据,K为初始流量指令改变量/稳态流量指令改变量。
利用电力系统综合分析程序 (PSASP)的用户自定义建模功能建立图5的协调控制系统模型,如图7所示。

图7 协调控制系统模型结构
图7中,滞后环节为一阶惯性环节,其惯性时间常数为 5.125 s。速率限制环节的限制值为30 MW/min,折算成标幺值为0.001 43。
汽轮机模型的主要参数通过对机组进行调速系统参数测试的动态扰动试验获得,其辨识的结果见表1。
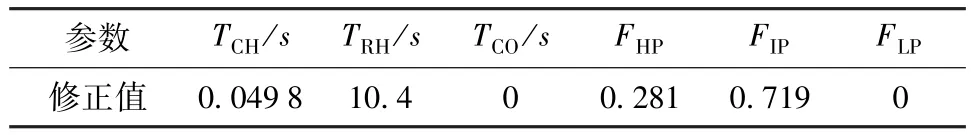
表1 汽轮机模型仿真的参数取值
2.2 改进模型的仿真校验
利用该机组一次调频试验数据,对改进模型进行仿真校验,校验结果如图8和图9所示。

图8 增负荷仿真曲线与实际录波

图9 减负荷仿真曲线与实际录波
图8、图9中,原始模型由于未考虑阀门流量特性的影响,仿真曲线与实际录波存在一定的偏差。而计及阀门流量特性的修正模型则能够与实际录波更好地吻合,如果考虑到对阀门流量特性线性化处理引起的误差以及试验录波过程中的噪声干扰,计及阀门流量特性的修正模型的仿真曲线与实际有功功率响应的偏差可以忽略。
3 结论
1)在电力系统综合分析程序中,建立计及调节阀门流量特性的汽轮机调速器模型。对该模型进行仿真校验,仿真结果表明与原模型相比,改进模型能够更好地模拟实际机组的响应特性。
2)通过仿真发现,汽轮机调节阀门的流量特性对其功率响应过程有重要影响,因此当电液调节系统的阀门流量函数与实际阀门流量特性不匹配时,就必须考虑阀门流量特性对模型结构和仿真精度的影响。
〔1〕国家电网公司.电力系统四大参数对暂态稳定的影响 〔C〕.电力系统建模与仿真技术研讨会 〔C〕.长沙,2004.
〔2〕王官宏.原动机调节系统对电力系统动态稳定影响的研究〔D〕.北京:中国电力科学研究院,2008.
〔3〕西安交通大学.电力系统计算 〔M〕.北京:水利电力出版社,1978:312-350.
〔4〕朱方,汤涌,张东霞,等.发电机励磁和调速器模型参数对东北电网大扰动试验仿真计算的影响 〔J〕.电网技术,2007,32(4):69-74.
〔5〕徐衍会,贺仁睦,孔祥云.调速系统超速保护控制对电力系统稳定的影响 〔J〕.现代电力,2006,23(6):6-9.
〔6〕宋新立,刘肇旭,李永庄,等.电力系统稳定计算中火电厂调速系统模型及其应用分析 〔J〕.电网技术,2008,32(23):44-49.
〔7〕于达仁,郭钰峰,王晓娟,等.计及回热器蓄热效应的汽轮机动态模型 〔J〕.中国电机工程学报,2005,25(14):8-88.
〔8〕田云峰,郭家阳,刘永奇,等.用于电网稳定性计算的再热凝汽式汽轮机数学模型.电网技术,2007,31(5):39-44.
〔9〕李劲柏,刘复平.汽轮机阀门流量特性函数优化和机组安全性经济性的影响.中国电力,2008,41(12):50-53.
〔10〕中国电力科学研究院.电力系统综合分析程序 (PSASP)用户手册 〔Z〕.北京:中国电力科学研究院,2001.

