基于边移除的智能电网级联故障鲁棒性分析
,
(南京邮电大学 自动化学院,南京 210046)
0 概述
近年来,全球范围内发生了多起大规模连锁性停电事件。例如,2015年3月27日,荷兰一所变电站因技术故障,发生连锁故障导致荷兰大面积停电,对北荷兰等地区造成严重影响。2012年7月30号,印度三大电网相继瘫痪,大停电持续近2 d后才逐步恢复正常,印度境内超过一半地区电力供应受到影响,波及多达6亿多人。随着科技发展,现代生产生活对电力依赖程度越来越高,大面积停电不仅给日常生活带来不便,更对航空、铁路、城市交通、供水等造成严重影响。
国内外学者从各个方向和角度,通过理论建模和数据分析,对连锁大停电的机理展开广泛而深入的研究[1-3]。研究表明,事故往往由少数薄弱环节的故障引发,继而在电网中发生级联故障导致。研究主要集中在两大类,一类基于经典电路理论(如基尔霍夫定律)和电网电气特性的研究[4-6],关注于电网的物理特性,以阻抗或电抗作为权重,对各个元件进行详尽的数学分析,例如文献[6]构建了一种隐形故障的仿真模型,主要考虑断路器和继电保护设备的拒动或误动。这类在分析节点数较大的网络时会消耗大量的计算机资源。另一类基于电网拓扑结构的分析[3,7-9],例如文献[3]研究了不同网络拓扑结构和增长模式对级联故障的影响,文献[9]提出了一种基于区域恶劣气候影响下的电网级联故障模型。随着研究的深入,网络模型从单一的电网模型演化为电网和信息网二元融合的网络[7-8,10-11],文献[7]在2010年发现并探索了在电网和信息网双层网络中信息网对电力网络的影响。文献[10]发现双层网络中的信息交流可以有效减轻级联故障对电网的影响。其中部分研究采用了渗流理论[11],也有部分采用了图论[12-14]。这类研究从拓扑结构的角度考虑了智能电网的级联故障,关注于电网的整体特征和动态行为,研究拓扑特征参数和系统行为的内在联系。
以上这2种方法互有欠缺:1)在基于经典电路理论的建模中,各元件的个体动态特性起到了决定性的作用,元件特性的微分代数方程的求解消耗大量计算机资源,例如文献[15]对电网负载平衡和分散控制的研究中,由于计算较复杂,只能在节点数较少的电网中验证;2)基于复杂网络的建模将电网进行抽象和简化,主要关注于电网的统计学特性,电网的物理特性考虑不全面,文献[9,13]采用线路的电抗值作为线路的权重参数。线路电抗值是线路的固有属性,是一个静态的量,不能反映出电网的动态特性和线路的潮流特性。3)在以往的电网模型中,较少考虑电网的发电站、传输站和接收站各自的特性,将发电站、传输站和接收站归结为同一类型的站点。
针对第1)个问题,本文将电网抽象成点和边的集合,建立出无向加权网络图。利用复杂网络的理论研究电网的特性不仅可以大大简化计算复杂度,而且能从宏观的视角研究级联故障的特性。针对第2)个问题,国内外资料显示,线路有功潮流的大规模转移和线路过载是电网发生级联故障的主要原因[16]。因此,本文采用电网线路的有功潮流值作为初始网络的权重参数,以初始网络计算出的边介数作为边的负载,级联故障后会导致网络的拓扑结构发生变化,所有边的负载需重新计算,变化的范围是整体的而不是局部的。针对第3)个问题,级联故障后,电网可能分裂成互不连通的若干个小区域,将这些区域称为子图。若子图不含发电站,子图的供电发生中断,子图中所有节点和边都将失效。本文还研究了移除含有一个发电站的边,含有2个发电站的边以及不含发电站的边对网络鲁棒性的影响。
1 复杂网络级联故障仿真模型的建立
1.1 电力网络模型
电网特性可以从物理电气特性和网络拓扑结构两方面进行分析。在建立初始网络时,利用潮流值作为网络中传输线的权值。设任意2个站点i、j之间的潮流值用fij表示,fij可通过潮流计算得出。潮流计算为根据给定的电网结构、参数和发电机、负荷等元件运行条件,确定电力系统各部分稳态运行状态的参数,运行状态参数包括电网各母线节点的电压幅值和相角,以及各支路的功率分布、网络的功率损耗等。计算出的潮流矩阵F={fij}表示各支路的功率分布。为简化模型,本文采用DC直流潮流模型,即假设传输线在传输电能时无功率的损耗且忽略电压之间的相角,采用牛顿法求解电网的潮流矩阵。
设Vi和Vj为站点i和j的电压值,θij为站点i和j的电压相角差,rij为站点i和j之间的电阻。正常运行的电力系统各节点电压通常在额定电压附近,可近似认为Vi=Vj=1;线路两端电压相差值很小,因此,θij≈0;超高压网络中,线路电阻比阻抗小的多,电阻可以忽略,即rij=0,因此,站点i和j之间的有功功率和无功功率为:
(1)
站点i和j之间的有功功率fij即为对应的潮流值。bij=-1/xij,xij为支路电抗。对站点i用基尔霍夫定律可得:
(2)
对n节点网络写成矩阵形式为:
F=Hθ
(3)
其中,F为节点有功功率矩阵,即网络的潮流矩阵,H为n×n矩阵,其对角元素和非对角元素分别为:
(4)
用式(3)得到各站点的电压相角,再通过式(1)即可计算出各支路的潮流值。
将网络构建成以发电站,传输站和接收站为不同类型的顶点,以传输线为边,传输线的潮流值为权值,节点数为N,边数为M的无向加权图G=(V,E),其中发电站的顶点集合为S={s1,s2,…,sn1},传输站的顶点集合为T={t1,t2,…,tn2},接收站的顶点集合为R={r1,r2,…,rn3},图G的顶点集V={S,R,T}={i1,i2,…,iN}(N=n1+n2+n3)为发电站,传输站和接收站的集合。边集E={e1,e2,…,eM}表示电网中所有传输线的集合。aij表示G中站点i和j之间是否有边相连。若有边相连,这条边的权值为i和j之间的潮流值fij,若没有,为0,即:
(5)
其中,A={aij}为式(5)所组成的邻接矩阵,A为初始网络。
在电网中,电能沿着电气距离最短的路径传输,因此任意2个节点间存在一条最短连通通路。效率最高的最短连通通路往往为2个节点或边的最短路径,本文将边的初始负载定义为边介数的大小。网络中边介数为所有最短路径中经过该边的数目与最短路径总数的比值,边介数反映了边对电网功率的传输能力。
边(i,j)的初始负载定义为:
(6)
(7)
(8)
(9)

考虑到每个边处理负载的容量都有限度,即最大负载,超过最大负载,传输线失效,边从网络中移除。本文以耐受性参数衡量边的最大负载的能力,将最大负载定义为边初始负载的α倍,α即为这条边的耐受性参数,边(i,j)的最大负载定义如下:
(10)
对应的最大负载矩阵为C={cij}。
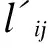
(11)
边将失效,若网络分裂为多个子图且子图中不含有发电站,则子图中的边都将失效。网络的拓扑结构发生变化,边的负载随之变化,即发生了级联故障。直到所有边的负载容量都小于其最大负载,级联故障停止。
1.2 移除策略
边权的定义有多种方法,其中边的介数在一定程度上反映了这条边的重要性程度。另外,边的重要性也与节点的重要性息息相关,当网络中边失效时,边两端的节点同时失效,因此结合节点重要性定义的方法,将边权定义为下面3种形式:
边权1(边的介数的大小) 计算公式为:
(12)
边权2(两端节点权值的算术平方根) 每个节点的权值为其对应的度和介数的算术平方根,即:
(13)
(14)
(15)
其中,Wi为节点i的权值,Ki为节点i的度,BCi为节点i的介数。
边权3(节点权值的算术平方根) 每个节点的权值为其对应度与其邻居节点度和的乘积,即:
(16)
(17)
(18)
其中,Ii、Ij分别为i、j邻居节点的集合。
为动态衡量网络级联故障的特性,本文对网络进行多次级联故障的仿真,每次根据策略移除其中一条边。多次连续级联故障中单次级联故障后,网络拓扑结构发生变化,重新计算边权,使边权的大小符合对应的网络拓扑结构。
单次级联故障仿真过程如下:
1)根据式(1)~式(4)计算每条边的初始潮流值,并根据式(5)确定网络的初始矩阵。
2)设定耐受性参数α,根据式(9)和式(10)分别计算网络中每条边的初始负载和最大负载。
3)选择不同的移除策略,若选择随机移除,则随机从网络中移除一条边;若选择目标移除,可根据式(12)、式(15)、式(18)分别选择边权1定义、边权2定义、边权3定义中权值最大的边。
4)移除相应的边后,若网络分裂为多个子图,且某个子图中不含有发电站,则移除这个子图中的所有边。
5)网络拓扑结构发生变化,重新计算网络中每条边的负载,若有边超过其最大负载,移除相应的边。
6)重复步骤4)、步骤5)直到没有边超过其最大负载,级联故障停止,衡量级联故障的发生程度。
多次级联故障仿真过程如下:
1)设定仿真次数k,进行单次级联故障仿真。
2)单次级联故障仿真结束后,若为目标移除,则可根据式(12)、式(15)、式(18)分别重新计算边权1定义、边权2定义、边权3定义中的边权,使边权的大小符合对应的网络拓扑结构。
3)重复步骤2),直到次数超过初始设定的仿真次数,多次级联故障仿真停止。
1.3 衡量指标
级联故障发生后,需采用一定的衡量指标来衡量级联故障发生的程度和网络鲁棒性。文献[17]提出了以网络效率来衡量网络G整体性能的指标。这一指标被广泛应用于网络级联故障的分析[18]。当电网中节点或边发生级联故障后,网络中节点对间的最短路径往往会发生变化,一些节点可能变成孤立节点,则此节点与其他节点的最短路径变成无穷大。这大大影响了网络的传输效率,网络的平均最短路径变大,网络效率变低。网络效率越高,网络的传输能力越强。本文采用网络效率下降百分比来衡量级联故障的大小,级联故障发生后网络效率下降百分比越少,网络鲁棒性越好。网络效率表示如下:
(19)
其中,E(G)为根据节点i到j的最短路径dis(i,j)定义的网络效率,n为网络中的节点总数,dis(i,j)为节点i,j间的最短路径长度。
与传统的路径长度的定义不同,网络效率的定义可以很好的衡量非连通网络。假设Damage(G,d)为在G中移除边d或者节点d之后的网络,则d使网络效率发生下降的程度可用ΔΦ-/Φ来衡量,其中ΔΦ-=Φ(G)-Φ(Damage(G,d))。
多次连续级联故障发生中单次移除边d后的级联故障网络效率下降百分比为:
(20)
其中,Ec为发生级联故障后网络效率,Ei为初始网络效率。
当网络效率发生下降的程度越高,即ΔΦ/Φ越大,表示在对d的移除时网络G越脆弱,发生级联故障后的网络效率下降百分比Pstage越小。
2 模型仿真与分析
对电网的拓扑结构进行分析的过程中发现电网的拓扑结构具有明显的小世界特性。分别构建与电网具有相同节点数和边数的随机网络,对IEEE57、IEEE118网络进行了分析。
由表1分析结果可知,具有相同节点数和边数的电网的平均路径长度与随机图接近,但平均聚类系数远大于随机图,因此,电网具有明显的小世界特性。
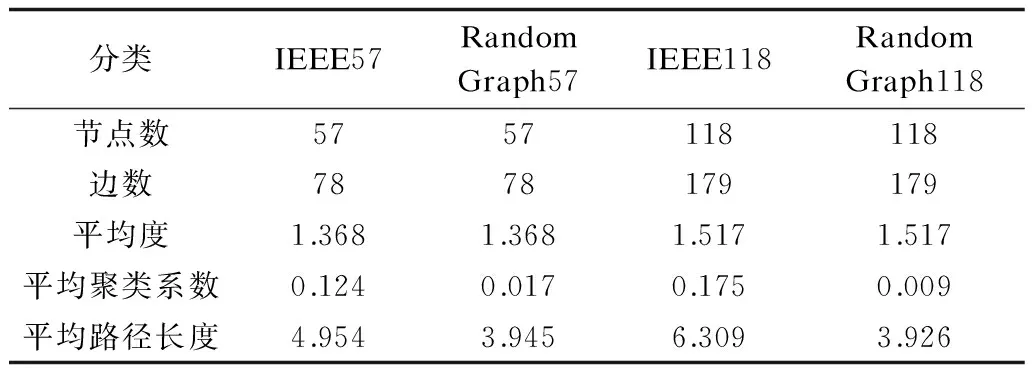
表1 不同节点网络及其对应的随机网络对比
2.1 网络级联故障分析
2.1.1 不同边移除策略对级联故障的影响
本文采用Matlab软件进行仿真,分别对网络IEEE57、IEEE118节点网络进行随机移除和目标移除。在随机移除时,随机选择一条边进行移除;在目标移除时,根据3种边权定义移除相应边权最大的边。单次级联故障后,根据式(20)计算网络效率下降的百分比Pstage。设置网络的耐受性参数α为1.5,多次级联故障次数k为15次。仿真图如图1所示。

图1 不同边移除策略下网络效率下降百分比
从图1(a)和图1(b)中可知基于边权1,边权2和边权3移除后网络效率下降百分比都比随机移除后下降的多,说明移除边权大的边会对网络鲁棒性有较大的影响。图1(a)中对IEEE118网络的仿真,网络效率下降的程度都比较均匀和平缓。对比可得基于边权3的移除策略网络效率下降的百分比最大,最终导致网络效率下降至0.2左右;基于边权1和边权2的类似,下降至0.3左右;基于随机移除策略的下降至0.4左右。进一步分析可得基于边权1和边权2的仿真在每一阶段移除的边相同或相似:15次的连续仿真过程中,基于边权1和边权2在前7次的阶段移除的边相同,后8次移除的边中有4次重合;基于边权1的移除在15次仿真过程中共有25个节点被移除,基于边权2的共有23个,在这些节点中2种边权策略被移除的重复的节点共有20个,因此,2种边权移除策略导致网络效率的下降具有高度相似性。图1(b)中,网络效率基于边权1和边权3的移除分别在第10次仿真阶段和第7次仿真阶段发生骤降,深入研究发现,这2个阶段都移除了边[48,49]。若不考虑边[48,49]对网络效率下降的影响,网络效率下降的百分比仅为0.1~0.15,说明边[48,49]对IEEE57网络的鲁棒性有很大影响。
2.1.2 网络中边权定义合理性的分析
对网络中的边依次进行移除,每条边的移除都将引发一次单次级联故障。选择一种边权定义,假设边集{ez=num|z∈M}中的边在此边权定义下边权都为num,则将移除此边集后的网络效率下降百分比进行平均得到Pstagenum,不同边权的边集得到网络效率下降百分比集合{Pstagenum|1≤num≤M},将网络效率下降百分比集合按序排列得到散点图,并进行回归曲线分析。在回归曲线中,边权定义越合理,回归曲线下降越快;对回归曲线中的异常点进行残差序图的分析,异常点越少,说明回归曲线越能合理拟合散点图,边权的定义也就越合理,边权越能反映边的重要性。
对IEEE118网络进行仿真,图2(a)为对基于边权1定义的边进行移除后网络效率下降百分比,图2(b)为对基于边权1定义的边移除后的残差序图。图3(a)为对基于边权2定义的边进行移除后网络效率下降百分比,图3(b)为对基于边权2定义的边移除后的残差序图。图4(a)为对基于边权3定义的边进行移除后网络效率下降百分比,图4(b)为对基于边权3定义的边移除后的残差序图。

图2 基于边权1定义的边的仿真

图3 基于边权2定义的边的仿真

图4 基于边权3定义的边的仿真
在图2(a)、图3(a)、图4(a)中,星型拟合直线为对所有的散点进行拟合的结果,三角型拟合直线为去除异常点后进行拟合的结果。曲线下降越快,说明移除相应边权定义的边后网络发生级联故障越严重,边权定义更能反映边合理性。对于不同边权的仿真,网络效率百分比都随着移除边权的增加而下降,其中边权1下降最多,在移除边权权值最高的边后,网络效率的下降达到0.2,边权2次之,达到0.5。在图2(b)、图3(b)、图4(b)残差序图中,三角型部分为异常点,即置信区间没有包含零点的点,异常点的数目越少,说明边权的定义越合理。对边权1仿真中,异常点数目为7个,边权2中有19个,边权3中有17个。边权1的仿真结果中异常点的数目明显少于边权2和边权3的仿真;对于边权1和边权2的仿真,异常点都分布在边权较大的边中,而边权3的异常点分布范围较均匀。综上所述,边权1的定义更能反映出边的合理性程度。
2.2 不同耐受性参数对网络级联故障的影响
设置不同的耐受性参数α∈(1,2),对边进行单次级联故障的仿真。根据移除策略选择随机移除或者目标移除;在目标移除时,选择相应边权定义中权值最大的边。具有不同耐受性参数α的网络发生级联故障的网络效率下降程度也有所不同,仿真图如图5所示。
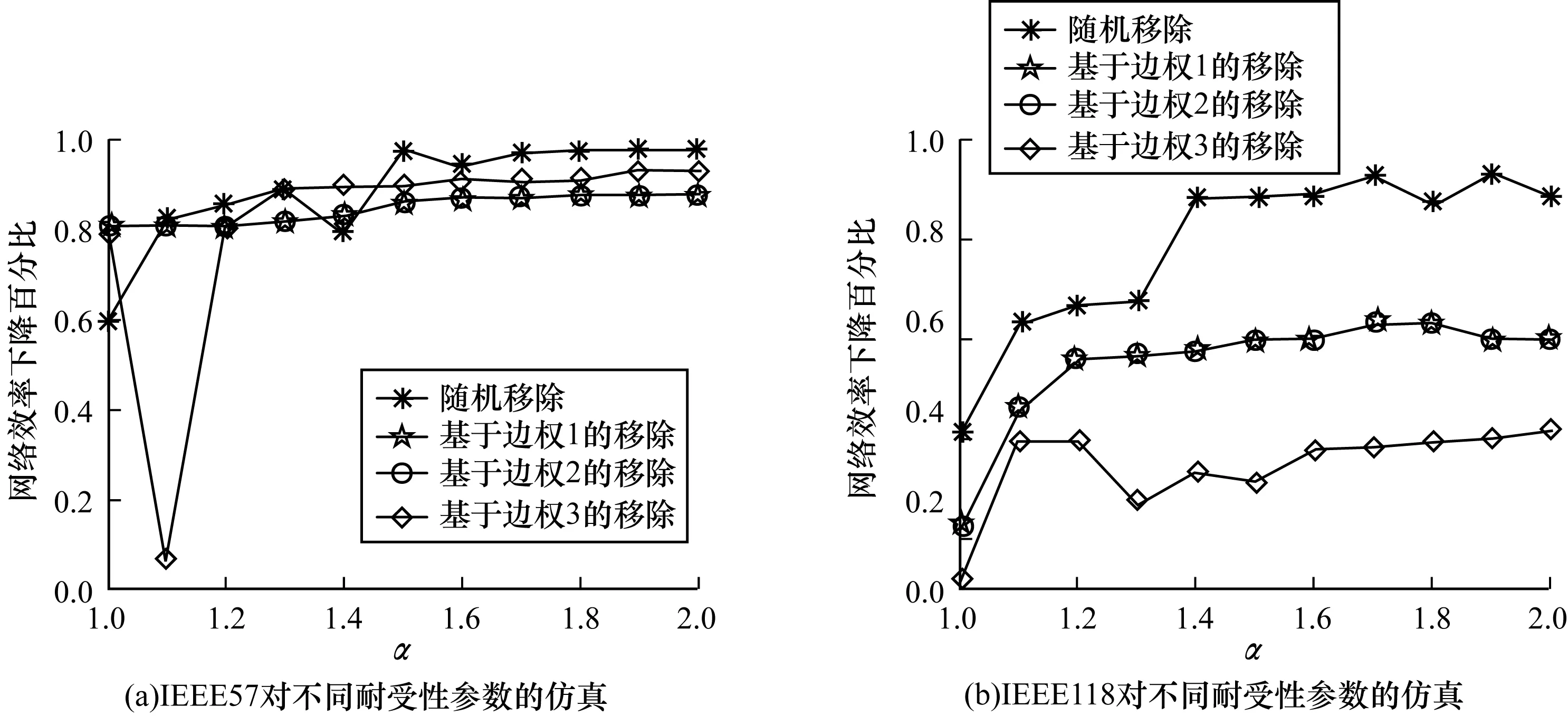
图5 不同耐受性参数对级联故障网络效率的影响
在图5(a)中,当α=1.1时,级联故障后网络效率出现较大程度的下降。深入分析可知,由于耐受性参数的变化,导致边[48,49]发生了级联故障,网络效率发生了较大程度下降;在边权1的定义中,边[48,49]的权值是相应最大边权权值的26.2%,在边权2的定义中,边[48,49]权值是相应最大边权权值的57.9%,边权3的定义中,边[48,49]权值是相应最大边权权值的53.2%,由此可见单独定义的边权的权值并不完全代表边对网络级联故障鲁棒性的影响。
在图5(a)、图5(b)中,对不同耐受性参数的仿真中,边权1定义和边权2定义的仿真几乎完全重合。分析可知,边权1和边权2定义的边权值大小具有相似性,因此多次级联故障中单次移除都是同一条边,仿真曲线几乎完全重合。对于不同网络,不同移除策略,网络效率的下降都在α∈(1.2,1.3)时趋于稳定,当耐受性参数由1变化至1.3时,级联故障后的网络效率上升至其最大值的90%左右,当耐受性参数由1.3变化至2时,级联故障后的网络效率没有发生很大变化,因此,实际电网中,把耐受性参数α设置为α∈(1.2,1.3)可用较低成本获得较大的网络鲁棒性。
2.3 含发电站边的移除
根据本文仿真模型的建立方法,若级联故障后网络分为多个子图且子图中不含有发电站,则这个子图中的所有边都将失效,因此,发电站占有重要作用。在2010年,文献[19]研究了智能电网中发电站的作用,得出增加少量发电站即可大大减少电网中级联故障的概率。文献[19]中的研究主要基于发电站站点的研究,本文从网络中边的角度,根据是否含有发电站,将边分为3类,分别为:1)有2个发电站的边;2)有一个发电站的边;3)不含发电站的边。相应的边集分别为{e2station|2station∈M},{e1station|1station∈M},{e0station|0station∈M}。对这3类边集分别进行移除,将移除边集后的网络效率下降百分比进行平均得到Pstageistation(i=2,1,0),不同边权的边集得到网络效率下降百分比集合为{Pstageistation|i=2,1,0},设置横坐标为耐受性参数α∈(1,2),纵坐标为网络效率下降百分比,仿真图如图6所示。由图6可知,移除含有2个发电站的边对网络鲁棒性的影响最大,移除含有一个发电站的次之,移除不含发电站的最小。图6(a)中,当耐受性参数为1时,移除不含发电站的边后级联故障的网络效率为0.85,移除含有一个发电站的边后网络效率为0.65,而移除含有2个发电站的边后网络效率仅为0.54。图6(b)中,当耐受性参数为1时,移除不含发电站的边后级联故障的网络效率为0.47,移除含有一条发电站的边后网络效率为0.46,而移除含有2个发电站的边后网络效率几乎为0,网络接近全部崩溃的状态。说明发电站对电网的鲁棒性具有非常重要的作用。
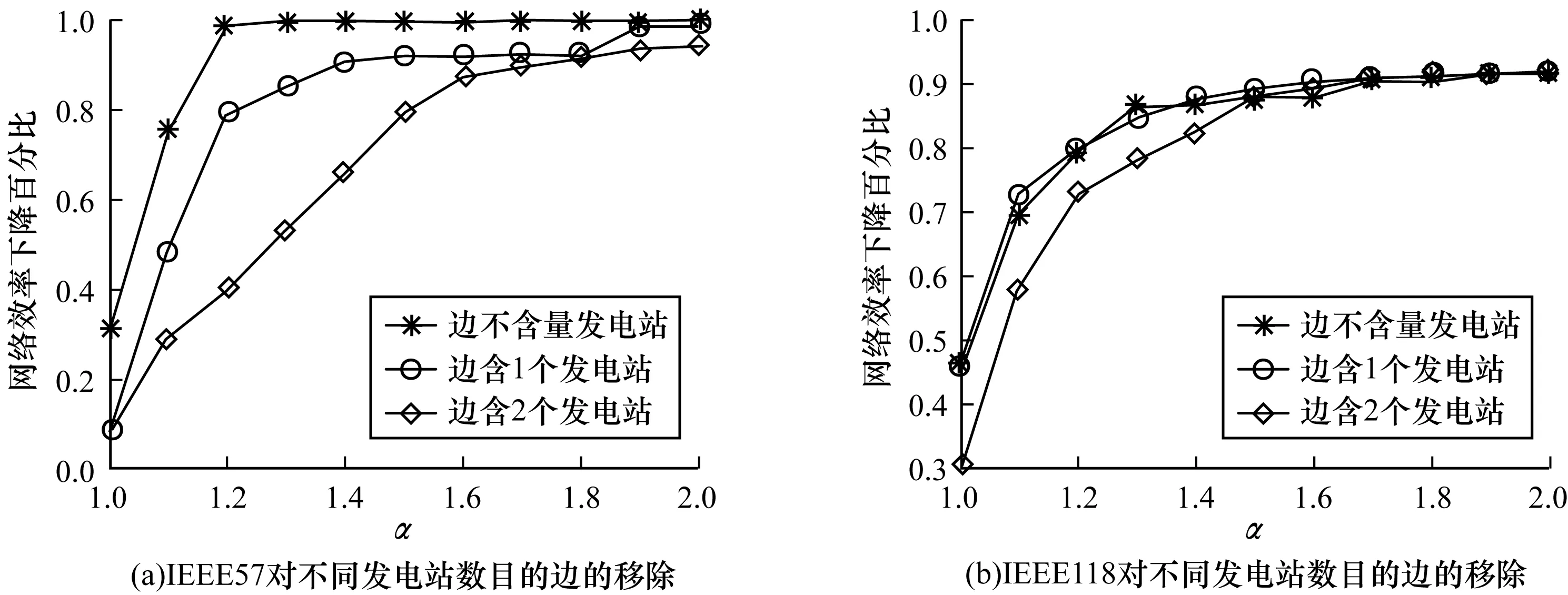
图6 对含有不同发电站数目的边进行移除的仿真结果
级联故障后的网络效率随着耐受性参数的增加而增加。α∈(1,1.6)时,网络效率快速增长,在α=1.6时,提升至其最大值的80%~90%,α∈(1.6,2)时,网络效率缓慢增长。在IEEE118网络中,当耐受性参数为1.6时,移除含有2个发电站的边后级联故障的网络效率由接近为0提升至近0.9,网络鲁棒性大大提升。因此,可通过增加网络的耐受性参数来增加网络的鲁棒性,以减少发电站对网络鲁棒性的影响。
3 结束语
本文从复杂网络的角度出发,结合电网实际的物理性质,提出一种基于电网拓扑结构的动态仿真模型。设置不同的边权定义,探索不同边移除策略对网络鲁棒性的影响,利用回归曲线分析网络中边权定义的合理性。进一步研究电网中耐受性参数对电网鲁棒性的影响以及发电站在电网拓扑结构中的重要作用。研究表明,边权越大以及边权定义越合理,移除这条边对电网鲁棒性的影响越大,但移除网络中某条边或某几条边,会导致网络的鲁棒性大幅下降。当耐受性参数发生变化时,随着耐受性参数的增大,网络的鲁棒性增强并趋于稳定。
[1] PAGANI G A,AIELLO M.The Power Gridas a Complex Network:A Survey[J].Physica A:Statistical Mechanics and Its Applications,2013,392(11):2688-2700.
[2] 范文礼,刘志刚.基于复杂网络的电网连锁故障模型研究综述[J].电力系统自动化,2012,36(16):124-131.
[3] PAGANI G A,AIELLO M.Power Grid Complex Network Evolutions for the Smart Grid[J].Physica A:Statistical Mechanics and Its Applications,2014,396(2):248-266.
[4] BLESOVSKY A.Power Grid Vulnerability to geographically Correlated Failures——Analysis and Control Implications[J].Proceedings——IEEE INFOCOM,2012,22(4):2634-2642.
[5] JUN Yan,TANG Yufei,HE Haibo,et al.Cascading Failure Analysis with DC Power Flow Model and Transient Stability Analysis[J].IEEE Transactions on Power Systems,2015,30(1):285-297.
[6] GARLAPATI S,HUA Lin,SAMBAMOORTHY S,et al.Agent Based Supervision of Zone 3 Relays to Prevent Hidden Failure Based Tripping[C]//Proceedings of IEEE International Conference on Smart Grid Communications.Washington D.C.,USA:IEEE Press,2010:256-261.
[7] BULDYREV S V,PARSHANI R,PAUL G,et al.Catastrophic Cascade of Failures in Interdependent Networks[J].Nature,2010,464(7291):1025-1028.
[8] HUANG Xuqing,GAO Jianxi,BULDYREV S V,et al.Robustness of Interdependent Networks Under Targeted Attack[J].Physical Review E:Statistical Nonlinear & Soft Matter Physics,2011,83(6).
[9] 和晨萍.基于复杂网络理论的电网脆弱性研究[D].南京: 南京理工大学,2014.
[10] WEI Mingkui,WANG Wenye.Combat the Disaster:Communications in Smart Grid Alleviate Cascading Failures[C]//Proceedings of High-capacity Optical Networks & Emerging/Enabling Technologies.Raleigh,USA:[s.n.],2014:133-137.
[11] ZHEN Huang,CEHGN Wang,RUJ S,et al.Modeling Cascading Failures in Smart Power Grid Using Interdependent Complex Networks and Percolation Theory[C]//Proceedings of Industrial Electronics and Applications.Melbourne,Australia:[s.n.],2013:1023-1028.
[12] KOÇ Y,WARNIER M,VAN M P,et al.A Topological Investigation of Phase Transitions of Cascading Failures in Power Grids[J].Physica A:Statistical Mechanics and Its Applications,2014,415:273-284.
[13] DWIVEDI A,YU Xinghuo,SOKOLOWSKI P.Identifying Vulnerable Lines in a Power Network Using Complex Network Theory[C]//Proceedings of IEEE International Symposium on Industrial Electronics.Seoul,South Korea:[s.n.],2009:18-23.
[14] LIANG Chang,WU Zhigang.Performance and Reliability of Electrical Power Grids Under Cascading Failures[J].International Journal of Electrical Power & Energy Systems,2011,33(8):1410-1419.
[15] SHI Benyun,LIU Jiming.Decentralized Control and Fair Load-shedding Compensations to Prevent Cascading Failures in a Smart Grid[J].International Journal of Electrical Power & Energy Systems,2015,67:582-590.
[16] CARRERAS B A,LYNCH V E,NEWMAN D E,et al.Blackout Mitigation Assessment in Power Transmission Systems[C]//Proceedings of Hawaii International Conference on System Sciences.Big Island,USA:[s.n.],2003:65-67.
[17] CRUCITTI P,LATORA V,MARCHIORI M.Locating Critical Lines in High-voltage Electrical Power Grids[J].Fluctuation & Noise Letters,2005,5(2):201-208.
[18] ZHU Lei,LIU Xiaochen,LU Yu,et al.Model of Cascading Failures for Communication Networks[J].International Journal of Computer and Communication Engineering,2016,5(5):302-310.
[19] XIAN Chen,DINH H,WANG Bing.Cascading Failures in Smart Grid-benefits of Distributed Generation[C]//Proceedings of the 1st IEEE International Conference on Smart Grid Communications.Washington D.C.,USA:IEEE Press,2010:73-78.
—— “T”级联

