电阻层析成像系统阵列电极宽度优化
肖理庆,王化祥,聂文艳
电阻层析成像系统阵列电极宽度优化
肖理庆1,2,王化祥3,聂文艳2
(1. 天津大学精密仪器与光电子工程学院,天津 300072;2. 淮南师范学院机械与电气工程学院,淮南 232038;3. 天津大学电气自动化与信息工程学院,天津 300072)
在电阻层析成像技术中,其他条件相同的情况下,不同宽度阵列电极对应的灵敏度矩阵不同. 为了提高算法反演精度,以敏感场均匀分布时灵敏度矩阵条件数的倒数为适应度函数,在优化有限元模型拓扑结构的同时,利用改进粒子群算法优化电阻层析成像系统阵列电极宽度,并将优化结果应用于改进牛顿-拉夫逊算法. 仿真实验结果表明,相比其他两种不同宽度阵列电极与拓扑结构的有限元模型,优化结果对应的灵敏度矩阵条件数分别降低了36.444,3%,和24.345,6%,,有效改善了灵敏度矩阵的病态性,从而提高了算法反演精度.
电阻层析成像;阵列电极;灵敏度矩阵;图像重建;病态性
电学层析成像技术包括电容层析成像[1-2]、电阻抗层析成像[3]、电阻层析成像(electrical resistance tomography,ERT)[4-6]和电磁层析成像[7-8]4种不同分支.其中,电阻层析成像技术目前已在医疗诊断、地球物理探测等领域获得了应用.
电阻层析成像技术逆问题求解属于典型的病态问题,即敏感场边界电压测量值的微小变化将导致算法重建图像较大扰动,甚至无法保证图像重建算法收敛.电阻层析成像技术逆问题病态的根源是灵敏度矩阵条件数很大(矩阵条件数越大,病态程度越严重),在相同实验条件下,灵敏度矩阵的病态程度是影响图像重建算法逆问题求解精度的主要因素.为了提高算法实时性,目前通常采用固定敏感场均匀分布时灵敏度矩阵不变的策略,而不同宽度阵列电极与拓扑结构有限元模型对应的灵敏度矩阵不同.文献[9]利用正交试验设计技术,对电阻层析成像系统的阵列电极数目、阵列电极宽度以及数据采集模式进行了优化设计;文献[10]设置了阵列电极6种不同的占空比:0.15、0.20、0.25、0.30、0.35、0.40,并结合共轭梯度算法图像重建结果选择电阻层析成像系统“最优”阵列电极宽度.与文献[9]存在的缺点相同,文献[10]中可供选择的阵列电极宽度数量较少,且没有考虑有限元模型拓扑结构对敏感场域内介质电阻率均匀分布时对应的灵敏度矩阵病态性的影响;文献[11]针对包含1,210个三节点三角形有限元、734个节点的有限元模型阵列电极进行了优化研究,但所采用的按等间隔原理剖分的均匀分布形式并非有限元模型最优拓扑结构;文献[12]通过优化电阻层析成像有限元模型拓扑结构,改善了灵敏度矩阵病态性,但没有考虑阵列电极宽度对敏感场域内介质电阻率均匀分布时对应的灵敏度矩阵病态程度的影响.
为了克服上述不足之处,笔者以敏感场电阻率均匀分布时灵敏度矩阵条件数的倒数为优化目标函数,在优化有限元模型拓扑结构的同时,利用计算量小、易编程实现的改进粒子群算法[13],优化电阻层析成像系统阵列电极宽度,降低了敏感场边界电压测量值微小变化对算法反演精度的影响,并通过仿真实验验证了优化措施在提高算法反演精度方面的有效性.
1 ERT阵列电极宽度优化
1.1 优化目标函数的确定
在相同实验条件下,不同宽度阵列电极与拓扑结构电阻层析成像有限元模型对应的灵敏度矩阵与正问题计算精度不同.虽然根据算法当前最优图像重建结果更新灵敏度矩阵有利于提高逆问题求解精度,但同时影响了算法实时性.另外,基于文献[12]通过仿真与实际实验验证所得的结论,笔者利用改进粒子群算法优化电阻层析成像系统阵列电极宽度与有限元模型拓扑结构时,最终确定的优化目标函数为

(1)

(2)
1.2 优化具体流程
利用改进粒子群算法优化电阻层析成像系统阵列电极宽度的具体流程如下.
步骤1建立传统按等间隔原理剖分的电阻层析成像有限元模型,完成节点与三角形有限元编号.
步骤 2 设置改进粒子群算法参数.
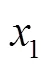
步骤4 根据各个粒子位置矢量,采取步骤3的方法调整三角形有限元节点位置,通过计算敏感场均匀分布时灵敏度矩阵条件数,判断解的优劣程度.
步骤5搜索电阻层析成像系统最优阵列电极宽度与有限元模型拓扑结构,其公式为
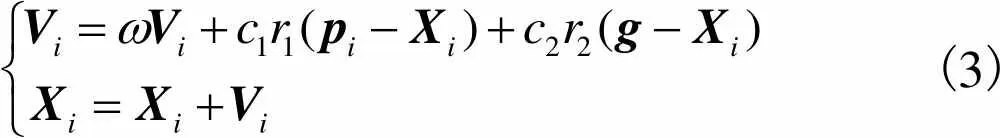
(3)
步骤6 判断是否满足结束条件,若是,保存优化目标函数最大值粒子对应的有限元模型节点坐标以及敏感场域内介质电阻率均匀分布时对应的灵敏度矩阵,否则跳转至步骤4循环计算.
由上可知,在笔者所提出的电阻层析成像系统阵列电极宽度优化方法中,通过调整三角形有限元节点位置,克服了文献[9-10]可供选择的阵列电极宽度数量较少的缺点,并通过所确定的优化目标函数,克服了文献[11-12]的不足之处.
2 仿真实验结果与分析
2.1 仿真实验条件
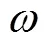
2.2 阵列电极宽度优化结果
利用改进粒子群算法在优化有限元模型拓扑结构的同时,优化电阻层析成像系统阵列电极宽度所得的目标函数最大值粒子对应的有限元模型如图1(c)有限元模型3所示.相比有限元模型1[14],有限元模型2、3灵敏度分布如图2和图3所示.
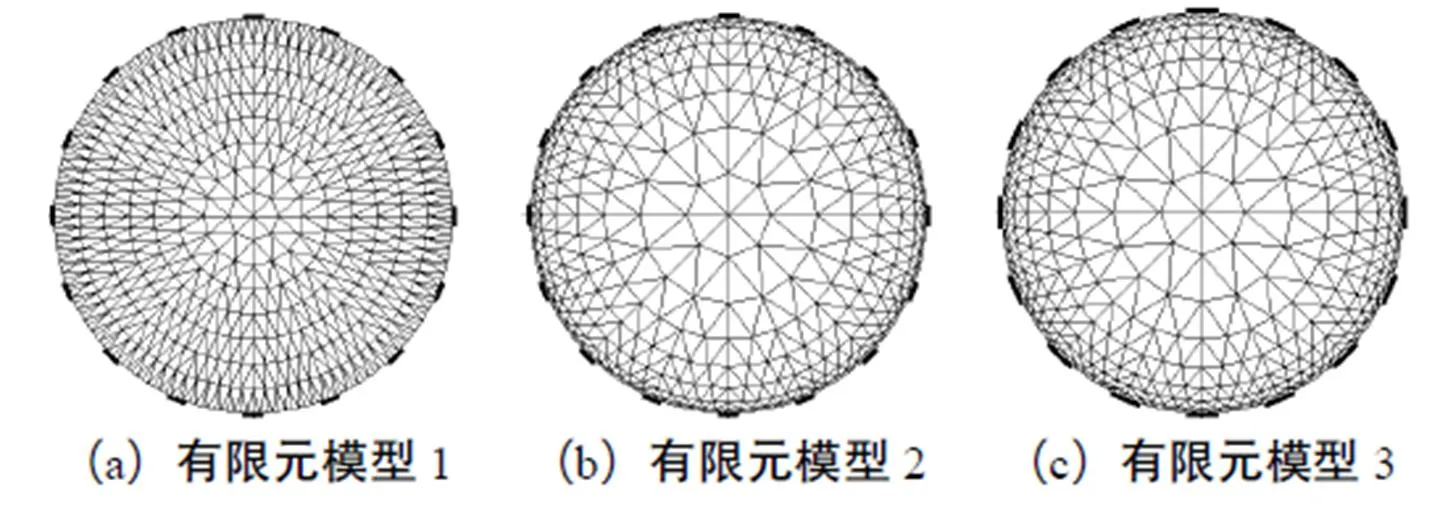
图1 有限元模型示意
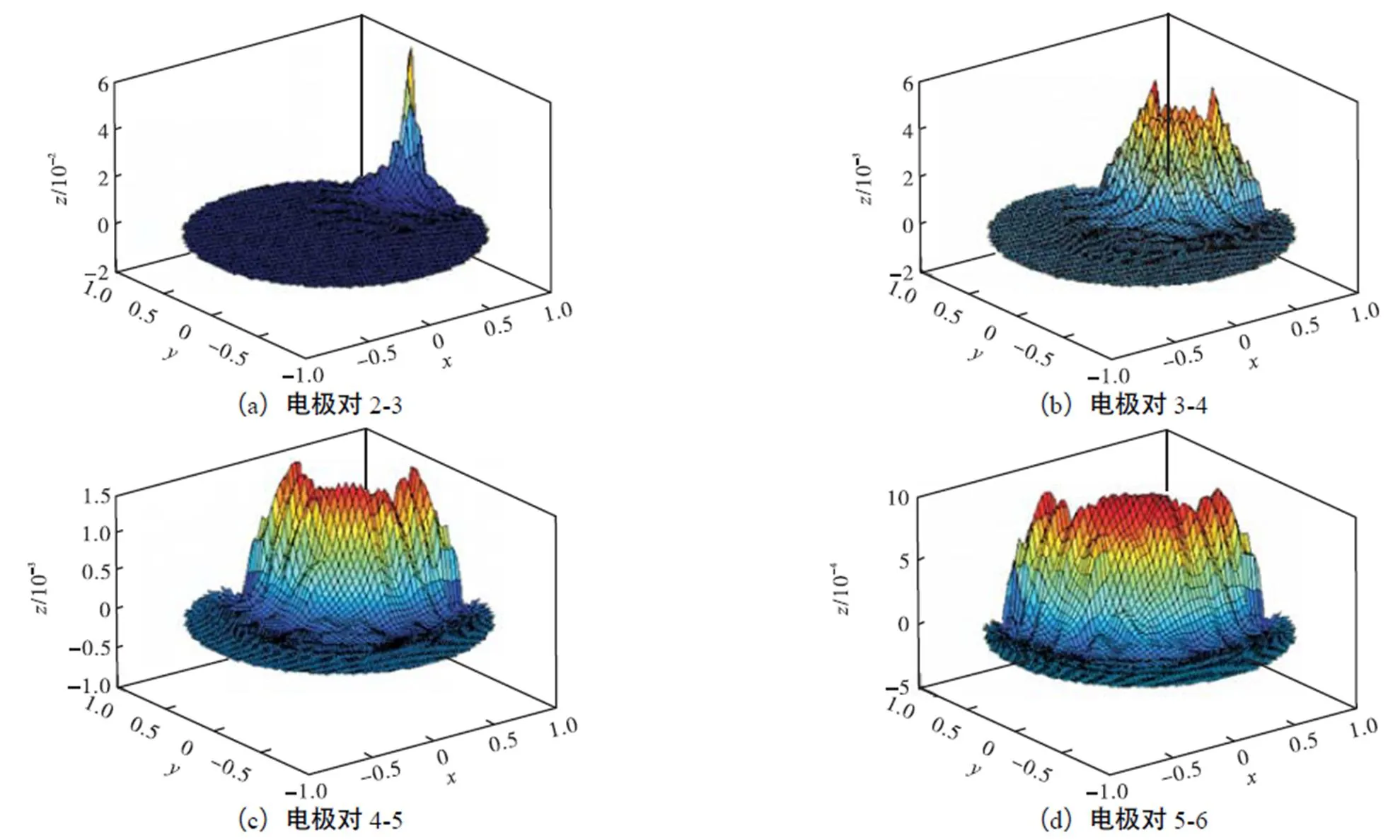
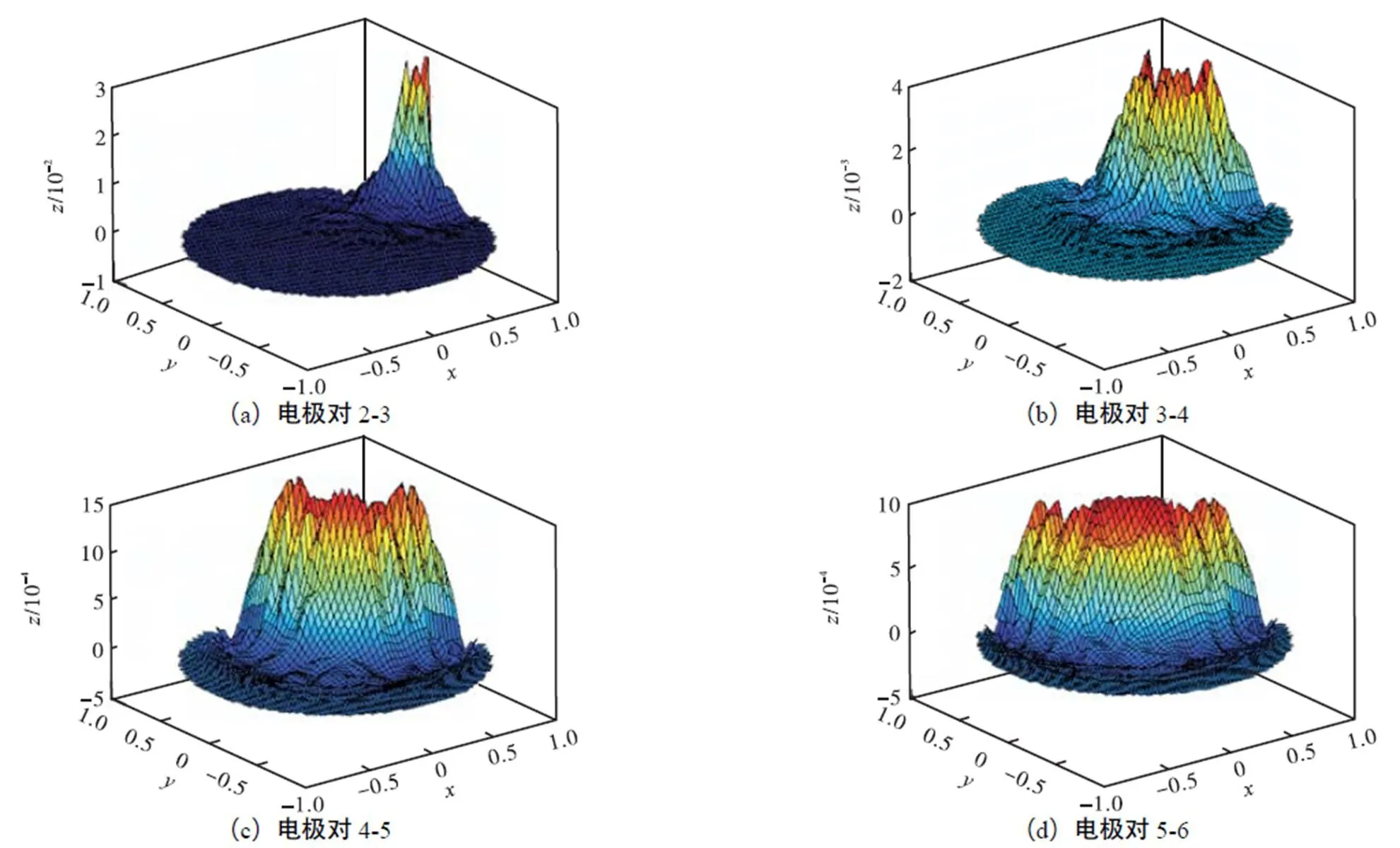
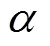
2.3 不同有限元模型图像重建结果
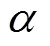
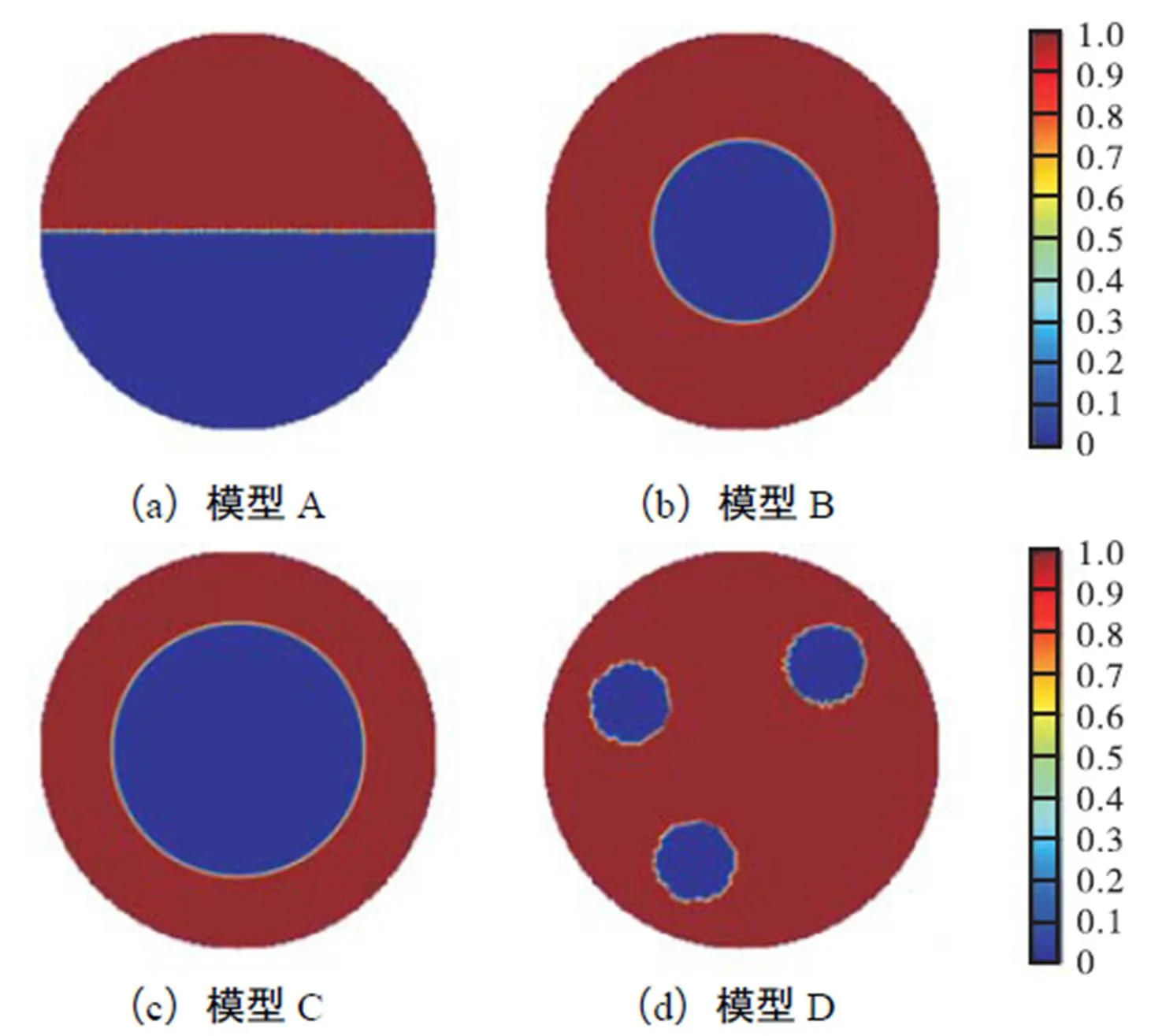
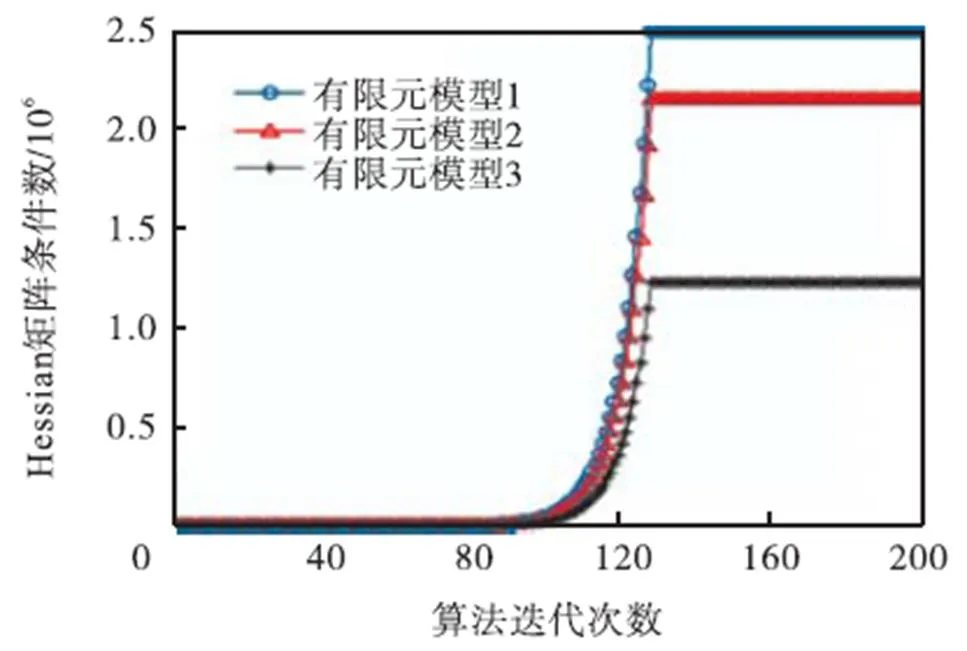
图5 Hessian矩阵条件数变化
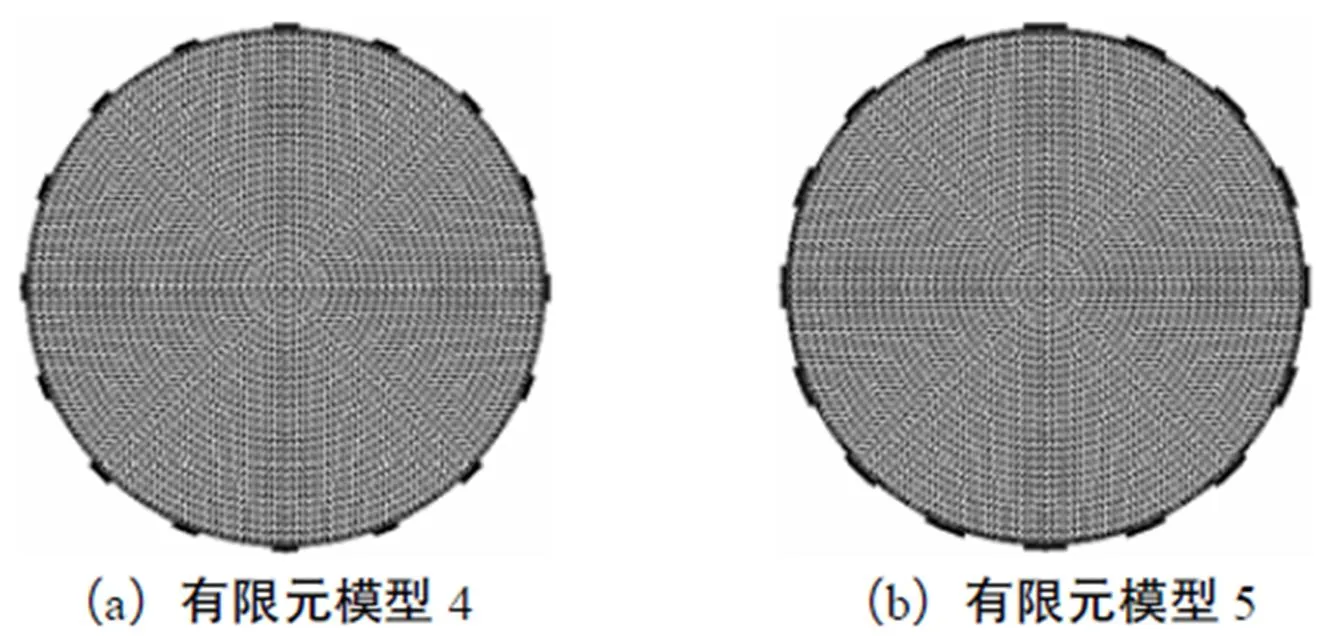
图6 计算正问题所采用的有限元模型
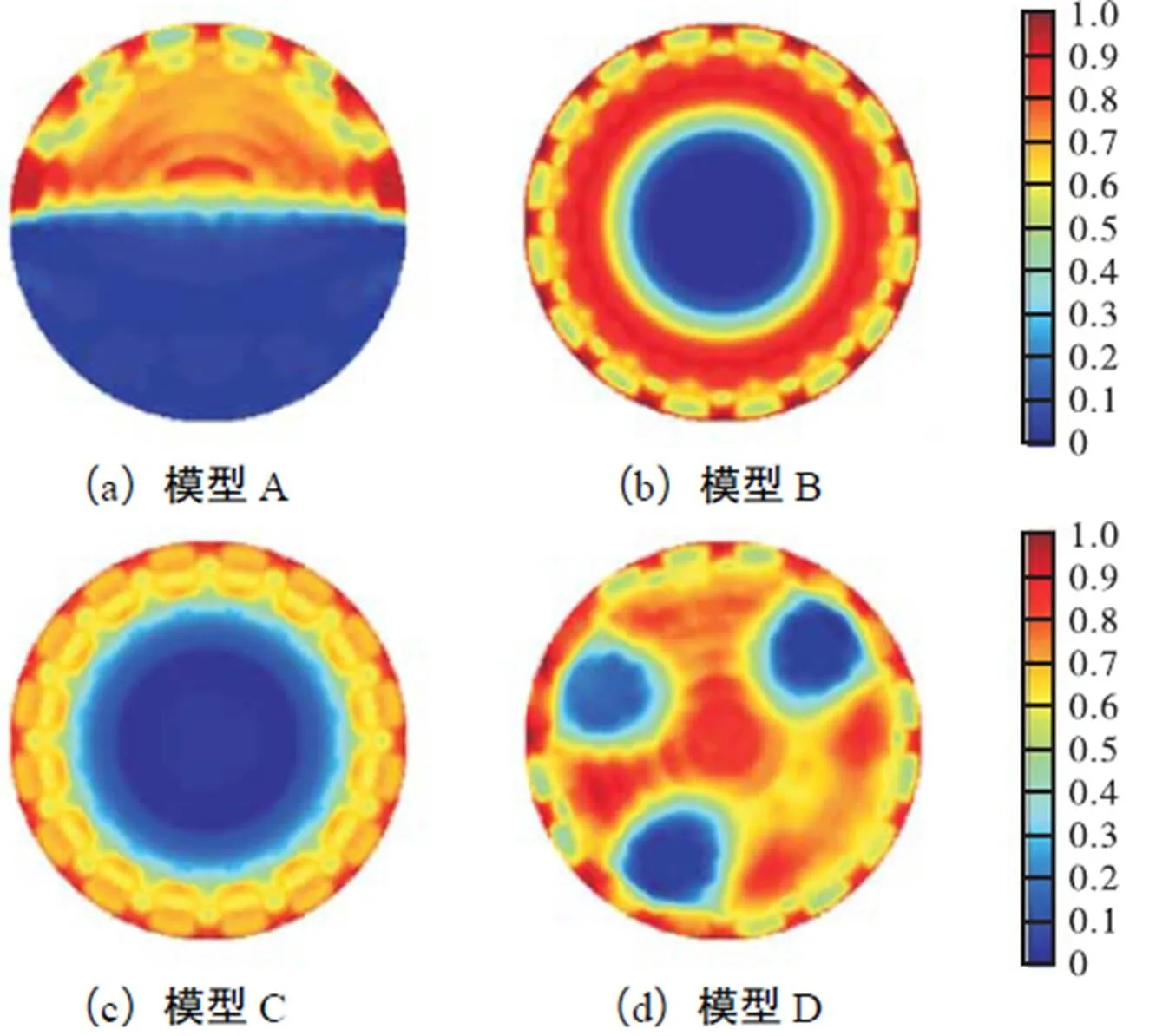
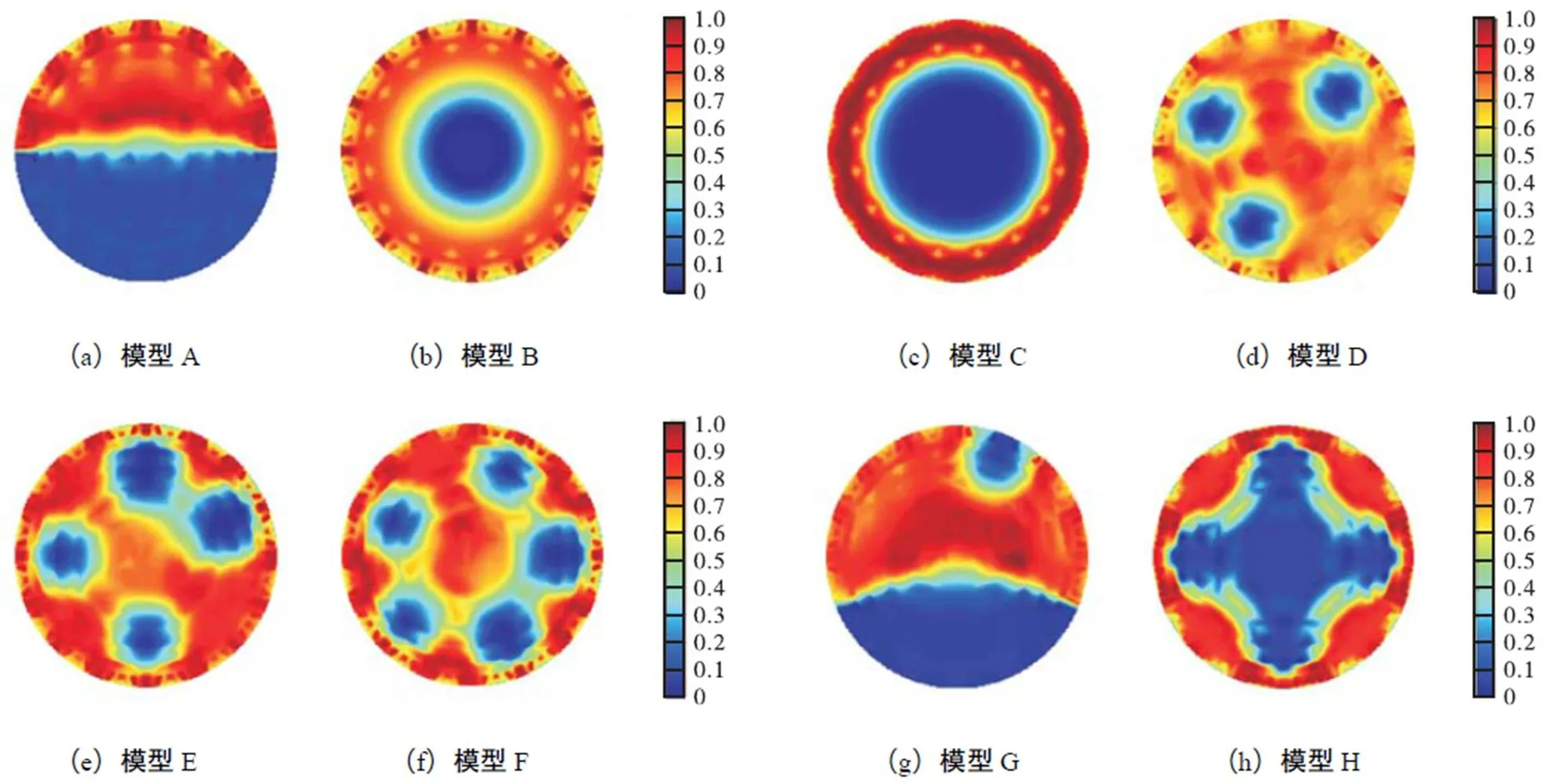
图8 有限元模型2重建结果
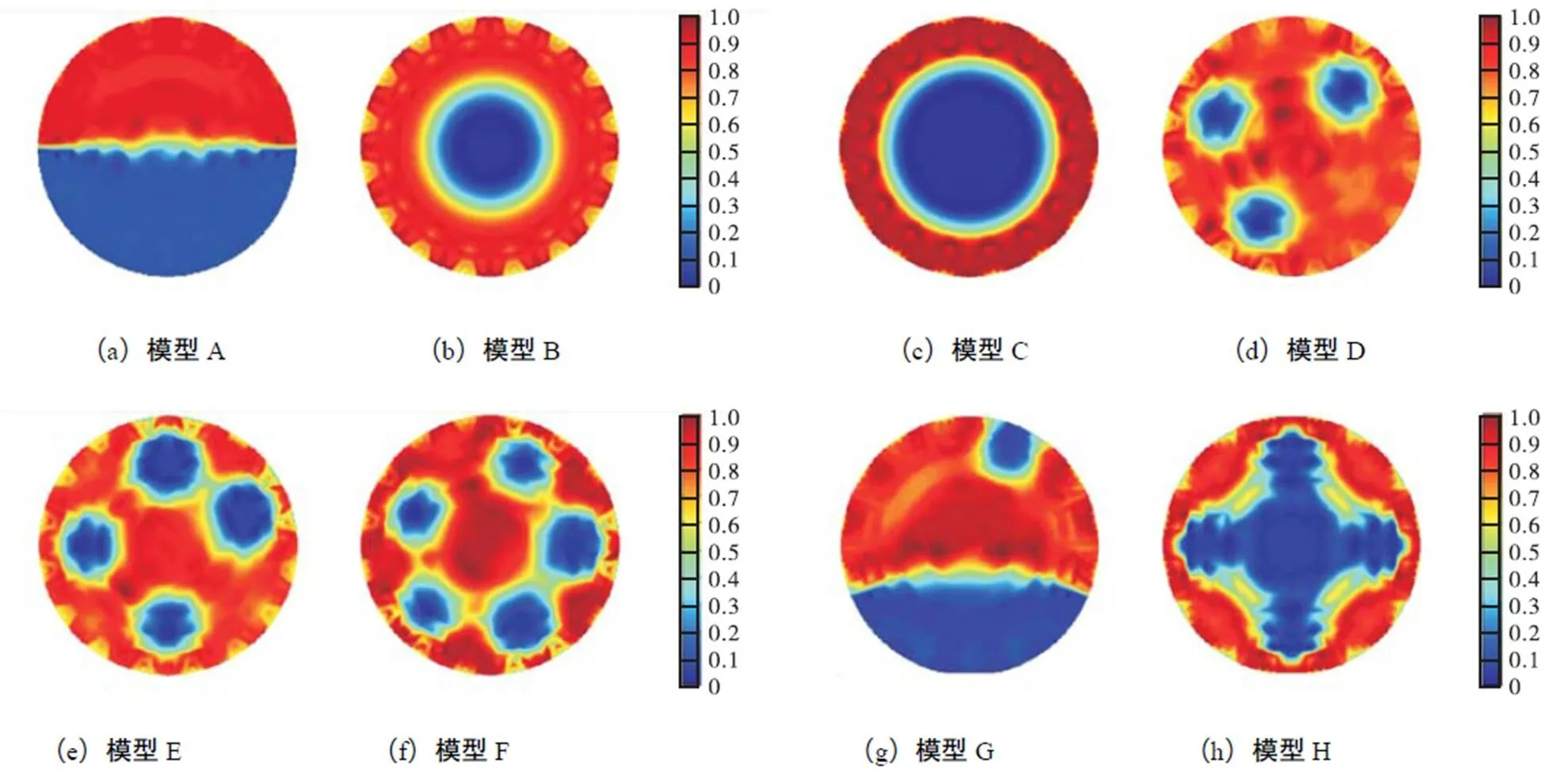
图9 有限元模型3重建结果
表1 相关系数比较
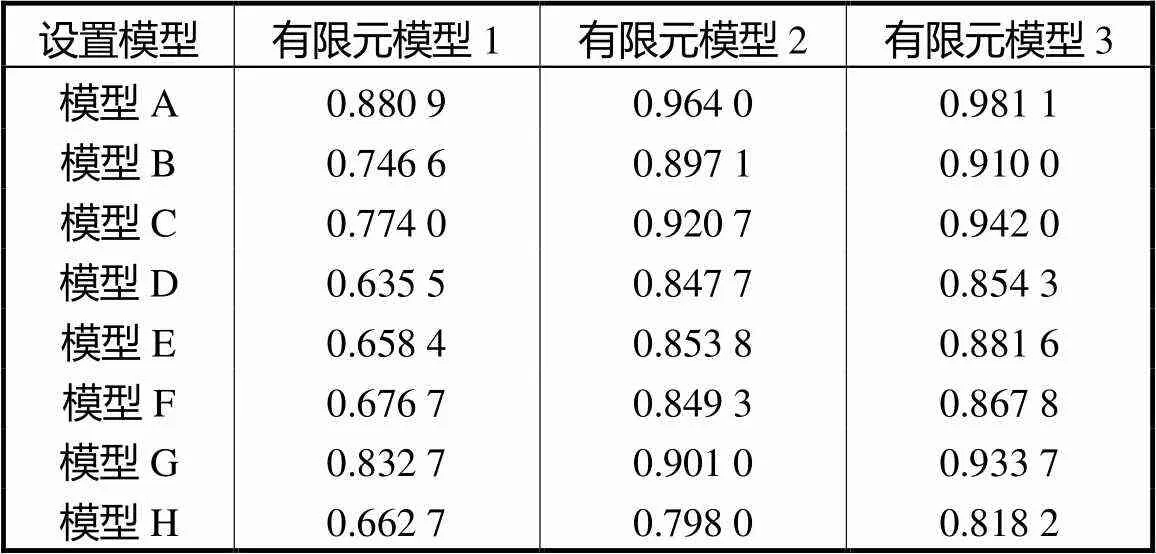
Tab.1 Comparison of correlation coefficients
其中,相关系数()与图像相对误差()是目前通常采用的两种评价重建图像质量的指标,其表达式[16]分别为
表2 图像相对误差比较
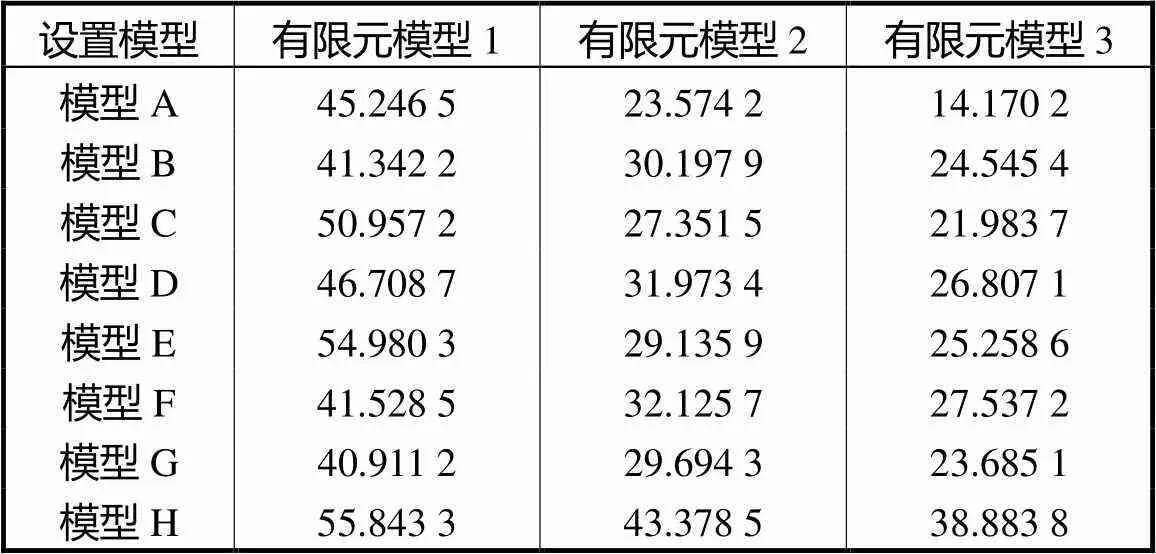
Tab.2 Comparison of image relative errors %
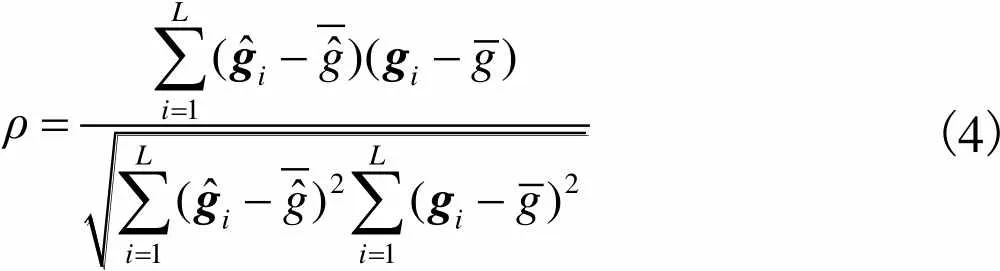
(4)

(5)
由表1可知,3种不同有限元模型相关系数平均值分别为0.733,4、0.879,0和0.898,6,相比有限元模型1、2,有限元模型3相关系数平均提高了22.525,2%和2.229,8%;由表2可知,3种不同有限元模型图像相对误差平均值分别为47.189,7%、30.928,9%和25.358,9%,相比有限元模型1、2,有限元模型3图像相对误差平均降低了46.261,8%,和18.009,0%.
为了检验不同有限元模型对测量噪声的鲁棒性,分别将图6所示的有限元模型4、5计算正问题所得的敏感场边界电压值加入5.0%,幅度随机噪声,以模拟系统噪声.不同有限元模型图像重建结果如图10~图12、表3和表4所示.
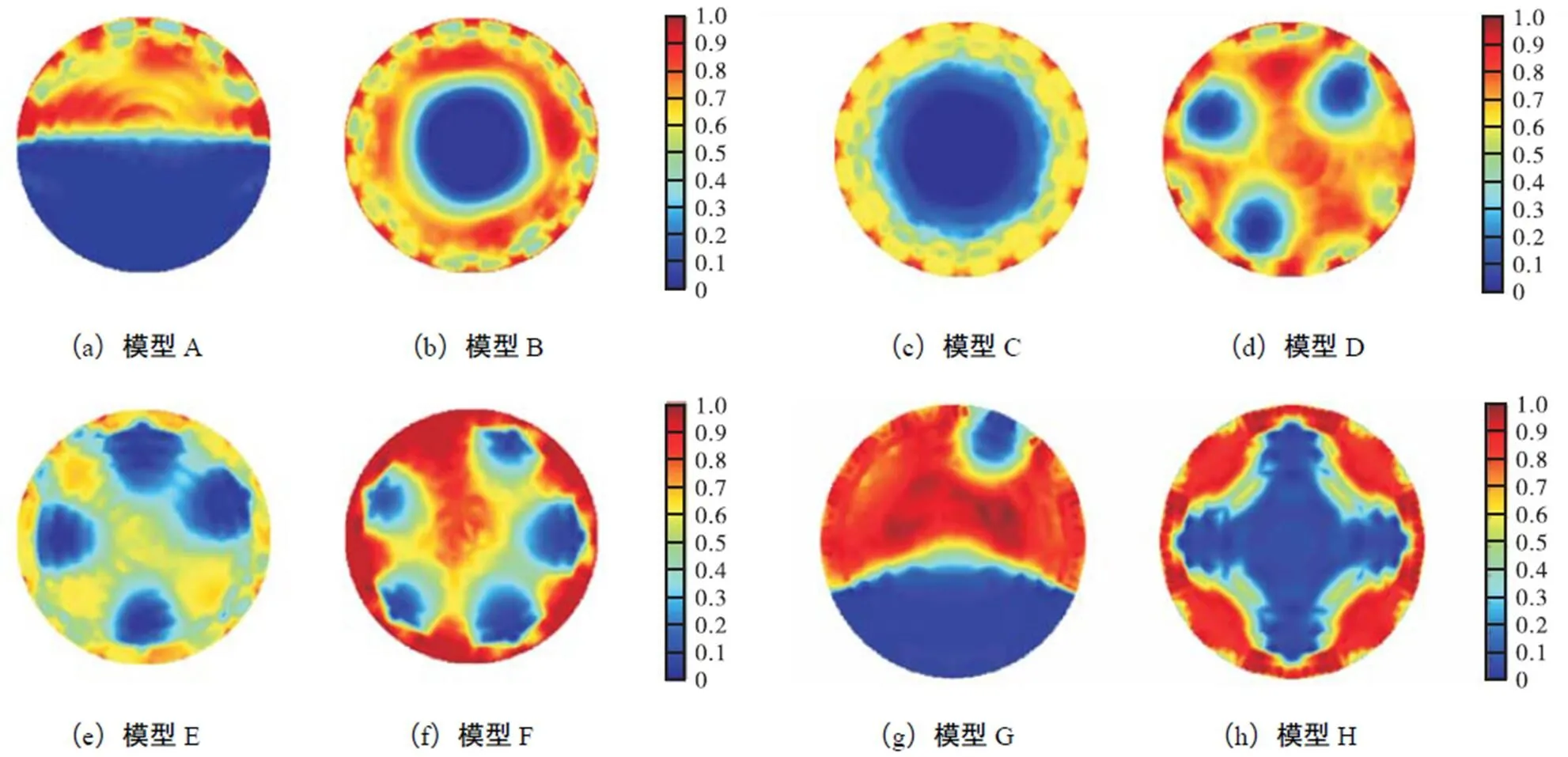
图10 噪声干扰下有限元模型1重建结果
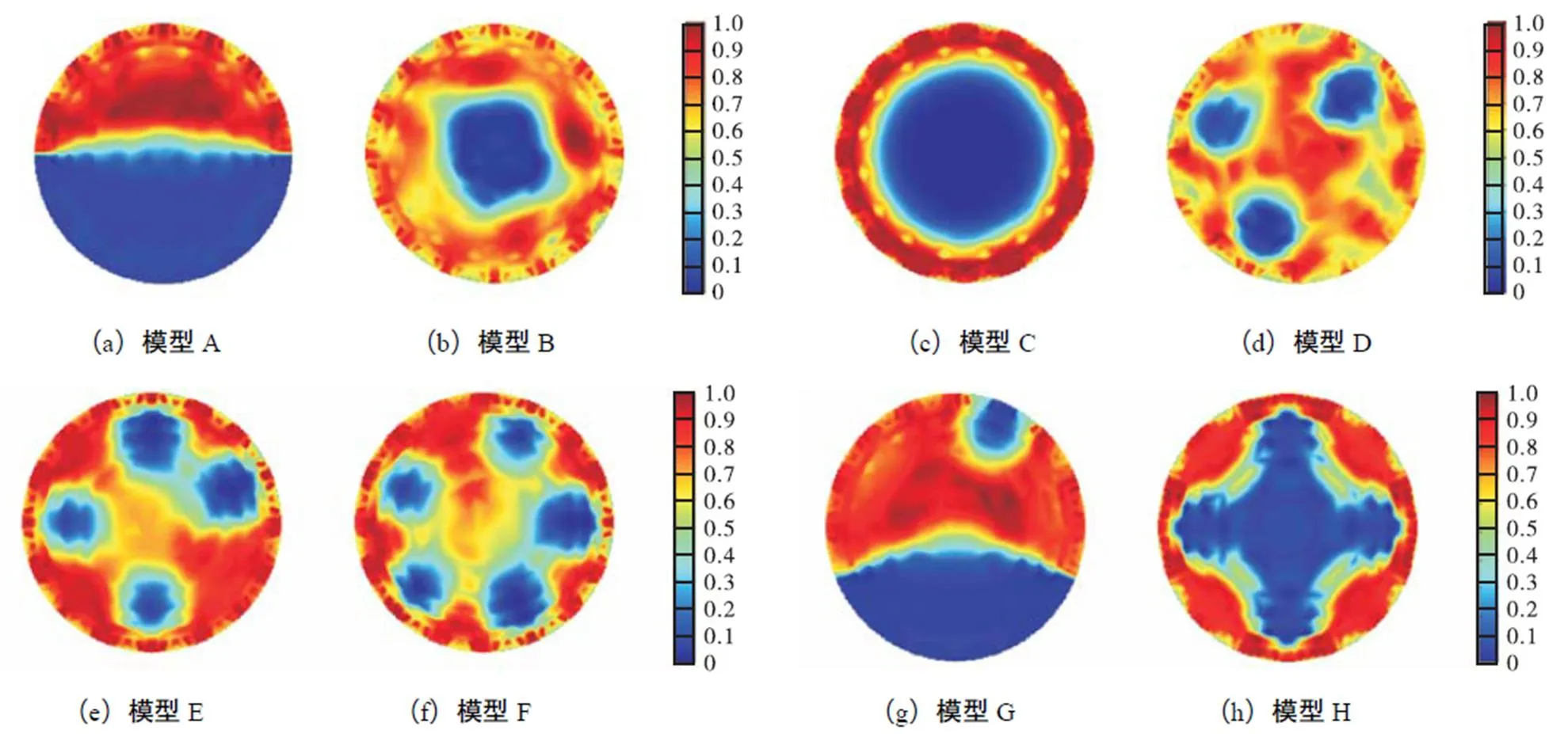
图11 噪声干扰下有限元模型2重建结果
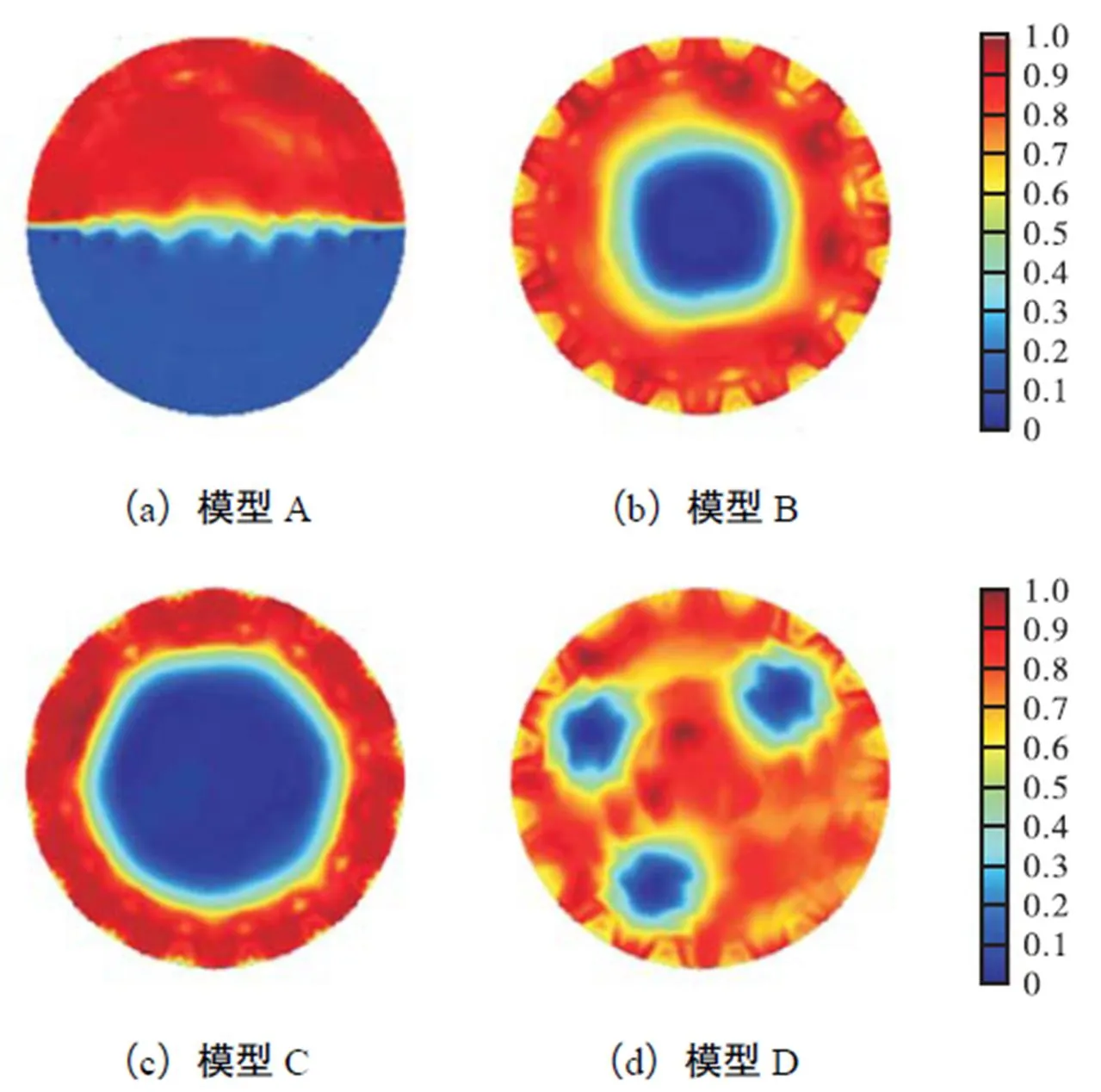
表3 噪声干扰下相关系数比较
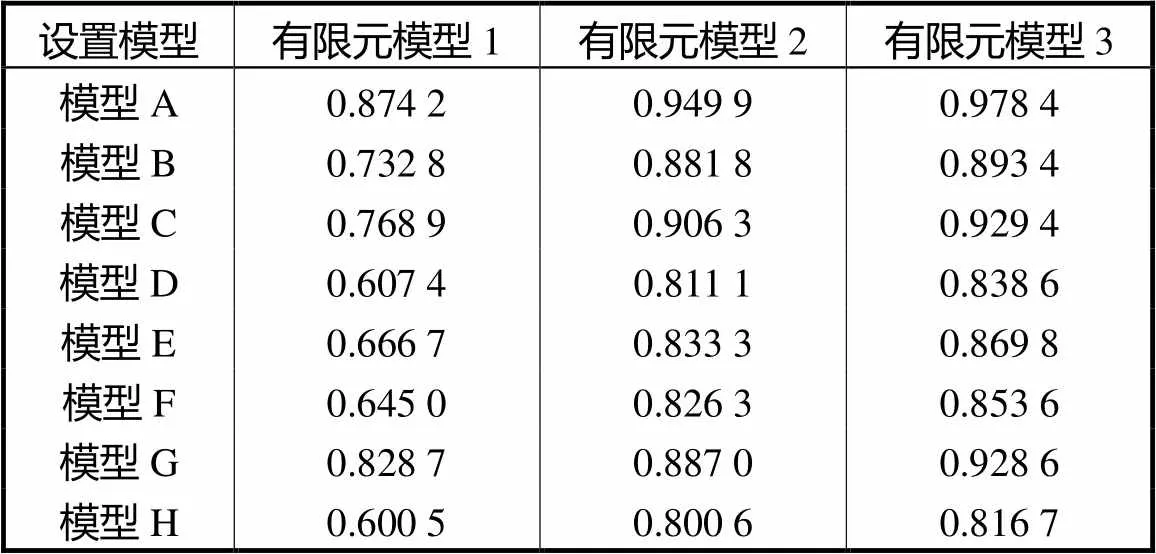
Tab.3 Comparison of correlation coefficients in the pres-ence of noise
由表3可知,3种不同有限元模型在5.0%,幅度随机噪声干扰下,相关系数平均值分别为0.715,5、0.862,0和0.888,6,相比有限元模型1、2,有限元模型3相关系数平均提高了24.192,9%,和3.085,8%,;由表4可知,3种不同有限元模型在5.0%,幅度随机噪声干扰下,图像相对误差平均值分别为50.519,6%,、32.951,3%,和28.003,5%,,相比有限元模型1、2,有限元模型3图像相对误差平均降低了44.569,0%,和15.015,5%,.相比有限元模型1、2,有限元模型3的图像重建精度最高,与无噪声干扰时结论相同.
表4 噪声干扰下图像相对误差比较
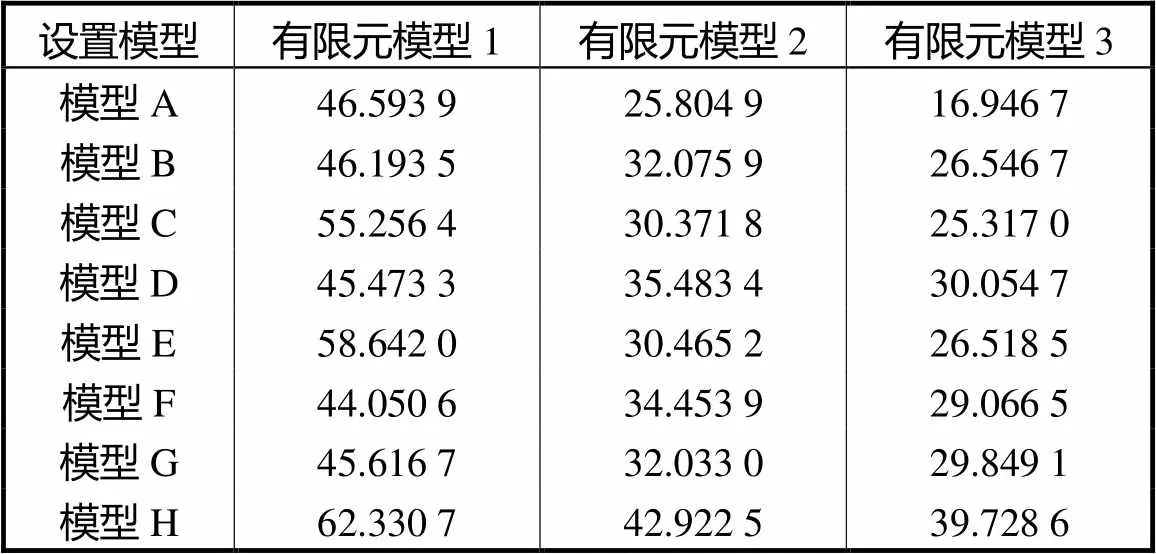
Tab.4 Comparison of image relative errors in the pres-ence of noise %
综上所述,在相同实验条件下,相比采取均匀分布形式的有限元模型及其改进模型,笔者在优化电阻层析成像有限元模型拓扑结构的同时,利用改进粒子群算法优化阵列电极宽度,降低了敏感场边界电压测量值微小变化对算法反演精度的影响,提高了重建图像分辨率.
3 结 语
为了提高反演精度,兼顾阵列电极宽度与有限元模型拓扑结构对敏感场域内介质电阻率均匀分布时对应的灵敏度矩阵病态程度的影响,笔者以其条件数的倒数为优化目标函数,利用改进粒子群算法在优化有限元模型拓扑结构的同时,优化阵列电极宽度,并将优化结果应用于改进牛顿-拉夫逊算法. 仿真实验结果表明,在相同实验条件下,相比采取均匀分布形式的有限元模型及其改进模型,敏感场域内介质电阻率均匀分布时对应的灵敏度矩阵条件数分别降低了36.444,3%,和24.345,6%,,有效降低了电阻层析成像敏感场边界电压测量值微小变化对算法反演精度的影响,提高了图像重建精度.
[1] 陈江涛,刘 石. 融合电容层析成像先验信息的集合卡尔曼滤波统计估计[J]. 化学工程,2012,40(4):36-39.
Chen Jiangtao,Liu Shi. Statistical estimation of ensemble Kalman filter fusion based on priori information approach in electrical capacitance tomography[J].,2012,40(4):36-39(in Chinese).
[2] Chen Qi,Liu Shi. Flame imaging in meso-scale porous media burner using electrical capacitance tomography [J].,2012,20(2):329-336.
[3] 陈晓艳,杨永政,杜 萌. 无解调电阻抗成像方法研究[J]. 传感技术学报,2015,28(6):870-875.
Chen Xiaoyan,Yang Yongzheng,Du Meng. Non-demodulation method study for electrical impedance tomography[J].,2015,28(6):870-875(in Chinese).
[4] 董 峰,赵 佳,许燕斌,等. 用于电阻层析成像的快速自适应硬阈值算法[J]. 天津大学学报:自然科学与工程技术版,2015,48(4):305-310.
Dong Feng,Zhao Jia,Xu Yanbin,et al. A fast adaptive iterative hard threshold algorithm for electrical resistance tomography[J].:,2015,48(4):305-310(in Chinese).
[5] Dong Feng,Xu Yanbin. Application of electrical resistance tomography in two-phase flow measurement[J].,2006,27(5):791-794.
[6] Daily W,Ramirez A. Electrical resistance tomography [J].,2004,23(5):438-442.
[7] Ma X,Peyton A J,Higson S R,et al. Hardware and software design for an electromagnetic induction tomography(EMT)system for high contrast metal process applications[J].,2006,17(1):111-118.
[8] Yin W,Peyton A J. A planar EMT system for the detection of faults on thin metallic plates[J].,2006,17(8):2130-2135.
[9] 魏 颖,于海斌,温佩芝,等. ERT传感器结构研究与优化设计[J]. 仪器仪表学报,2003,24(6):632-635.
Wei Ying,Yu Haibin,Wen Peizhi,et al. The research of sensor structure and optimum design for ERT[J].,2003,24(6):632-635(in Chinese).
[10] 王化祥,汪 婧,胡 理,等. ERT/ECT双模态敏感阵列电极优化设计[J]. 天津大学学报,2008,41(8):911-918.
Wang Huaxiang,Wang Jing,Hu Li,et al. Optimal design of ERT/ECT dual-modality sensing electrode array [J].,2008,41(8):911-918(in Chinese).
[11] Wang Yan,Sha Hong,Ren Chaoshi. Optimum design of electrode structure and parameters in electrical impedance tomography[J].,2006,27(3):291-306.
[12] Xiao Liqing,Xue Qian,Wang Huaxiang. Finite element mesh optimisation for improvement of the sensitivity matrix in electrical resistance tomography[J].,,2015,9(7):792-799.
[13] 张水平,仲伟彪. 改进学习因子和约束因子的混合粒子群算法[J]. 计算机应用研究,2015,32(12):3626-3628,3653.
Zhang Shuiping,Zhong Weibiao. Hybrid particle swarm optimization algorithm of new learning factors and constraint factor[J].,2015,32(12):3626-3628,3653(in Chinese).
[14] 肖理庆,王化祥,邵晓根. 基于模型细化改进牛顿-拉夫逊图像重建算法[J]. 仪器仪表学报,2014,35(7):1546-1554.
Xiao Liqing,Wang Huaxiang,Shao Xiaogen. Improved Newton-Raphson image reconstruction algorithm based on model refining[J].,2014,35(7):1546-1554(in Chinese).
[15] 何 为,罗辞勇,徐 征,等. 电阻抗成像原理[M]. 北京:科学出版社,2009.
He Wei,Luo Ciyong,Xu Zheng,et al.[M]. Beijing:Science Press,2009(in Chinese).
[16] Xue Qian,Wang Huaxiang,Cui Ziqiang,et al. Electrical capacitance tomography using an accelerated proximal gradient algorithm[J].,2012,83(4):1-7.
(责任编辑:孙立华)
Width Optimization of Array Electrode for Electrical Resistance Tomography System
Xiao Liqing1,2,Wang Huaxiang3,Nie Wenyan2
(1.School of Precision Instrument and Opto-Electronics Engineering,Tianjin University,Tianjin 300072,China;2. School of Mechanical and Electrical Engineering,Huainan Normal University,Huainan 232038,China;3.School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China)
In electrical resistance tomography(ERT),array electrodes of different widths lead to different sensitivity matrices,other things being equal.In order to enhance the inversion accuracy of the image reconstruction algorithms,the reciprocal of the condition number of the sensitivity matrix with homogeneous distribution of resistivity in the sensitive field,was designed as the fitness function,based on which the width of array electrode for electrical resistance tomography system and the topology of the finite element mesh were optimized using the improved PSO algorithm,and the best result obtained by the improved PSO algorithm was used to generate the sensitivity matrix,which was thereafter applied to image reconstruction using the improved Newton-Raphson algorithm.Simulation results demonstrate that,compared to the other two finite element meshes of different topologies and width,the condition number is reduced by 36.444,3%, and 24.345,6%,the ill-posedness is improved effectively,and thus it is propitious to enhance the inversion accuracy of the algorithm.
electrical resistance tomography;array electrode;sensitivity matrix;image reconstruction;ill-posedness
10.11784/tdxbz201602032
TK39
A
0493-2137(2018)01-0079-09
2016-07-29;
2016-09-06.
肖理庆(1981— ),男,博士,副教授,lqx1981@tju.edu.cn.
王化祥,hxwang@tju.edu.cn.
2016-09-22.
http://www.cnki.net/kcms/detail/12.1127.N.20160922.1443.012.html.
国家自然科学基金青年科学基金资助项目(61302122,61401466);江苏省高校自然科学研究面上项目(15KJB520033,16KJB470017,17KJB510053);安徽省高校优秀青年人才支持计划项目(gxyq2017060).
the Young Scientists Fund of the National Natural Science Foundation of China(No.,61302122 and No.,61401466),Project of Natural Scince Research in Universities in Jiangsu(No.,15KJB520033,No.,16KJB470017 and No.,17KJB510053),and Outstanding Youth Talent Support Program in Anhui University(No.,gxyq2017060).

