基于ADAMS仿形飞锯机锯切功率的分析与研究

梅克明，柴晓艳，马鲁豪，郑燕武

(1.天津理工大学天津市先进机电系统设计与智能控制重点实验室，天津 300384； 2.机电工程国家级实验教学示范中心(天津理工大学)，天津 300384)

0 前言

钢管广泛应用在国民经济建设中的各个领域。在钢管加工过程中，钢管飞锯机起到十分重要的作用，是生产线上将钢管随动锯切的设备，也是钢管加工制造过程中必不可少设备。

目前国内小管径的钢管机组配套的在线锯切设备以穿越式飞锯机为主，即当钢管与飞锯机同步时，锯片从上到下或从左到右横穿钢管，将钢管锯切成定尺长度。这种飞锯机的特点是设备的投资比较小，操作简单、容易掌握，具有良好的产品适应能力和较高的生产效率。但是，在锯切大管径钢管时，如采用穿越式飞锯机，会使得锯片与被锯切物体的摩擦力和噪音成为最大的阻力，故不再采用传统的加工方式，代之以新型的数控仿形飞锯机。该飞锯机采用多个小锯片，环绕钢管外围轮廓快速切断钢管，即节省能耗又降低噪声，还可以改善现场安全性和钢管加工质量。目前我国钢管加工企业已采用了这种设备，使用效果很好。

1 钢管仿形飞锯机工作原理

钢管仿形飞锯机的锯切系统主要是由大盘转动机构，刀盘自转机构和径向进给机构组成。在锯切系统上装有两到四个锯片，两个锯片结构如图1所示，采用两个各自独立的、带有驱动和进给的锯切机构，工作时首先径向进给机构进行径向进给，进给方向如图1箭头所示。当刀盘自转机构的锯片切透金属构件壁厚后，支撑两个锯片的大盘转动机构(图中未画出)开始旋转，同时锯切机构根据构件外形按预先设定的程序进行径向移动，以使锯片能够完全切断管壁又不致切入过深。每个锯片都只负责完成一半的锯切任务。

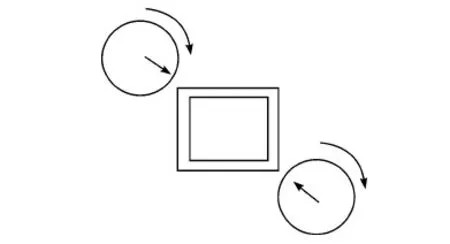
图1 锯切示意图

在锯切开始的时候，锯切的第一阶段为锯片沿直线切入，并切穿钢管，此阶段的切削功率变化不可避免，锯切的第二阶段即为锯片的周向移动，锯片沿着钢管的外轮廓进行锯切，两个锯片各自锯切接近180°，完成锯切。第三个阶段为锯片沿径向退刀，并返回初始位置。在全部锯切过程中，第一阶段的锯切功率的波动不可避免，第三阶段不存在锯切力，第二阶段则承受了大部分的锯切过程并且存在锯切功率的波动。所以需要对第二阶段的锯切过程进行分析。由于圆形钢管在锯切过程中锯切量恒定，锯切功率比较稳定，因此研究价值不大。而对于方管和异型管而言，由于其形状的不规律，因而切削功率的波动比较大，在这方面的研究比较缺乏。本文以方管为例，对钢管切削过程中钢管切削功率的变化规律予以分析研究。钢管的尺寸见表1。

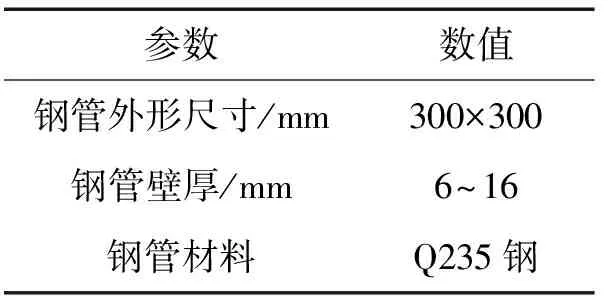
表1 钢管的相关参数

2 锯片相关参数选择与计算

锯片的锯切方式类似铣削。考虑到锯切钢管的外径(300 mm×300 mm)和钢管壁厚(6～16 mm)，以及实际机械加工的需要，选取锯片直径为275 mm。考虑锯片的厚度，应根据加工需求及锯片尺寸进行分析选择。锯片如果过薄，会导致锯片强度、刚度不足，在实际加工过程中，容易引起锯片的变形，降低锯片的可靠度。锯片厚度过大，会导致锯切力和锯切功率过大，降低锯切效率，造成资源的浪费。因此，选择合适的锯片厚度是十分重要，其大小应由锯片外径进行计算，即

(1)

式中，B为锯片厚度；D为锯片直径。

综合各方面因素考虑，锯片尺寸如表2所示。

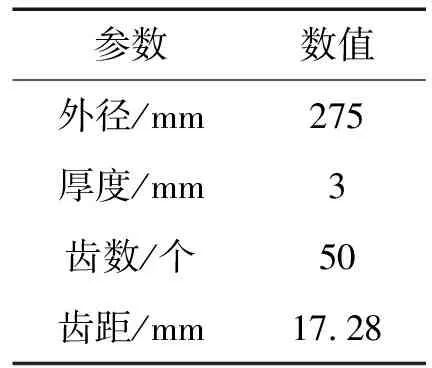
表2 锯片的基本尺寸

参考设计手册，拟定锯片转速n=200 r/min，由此可得锯片锯切速度为

(2)

2.1 每齿进给量与进给速度分析计算

仿形铣切的加工原理类似于铣削，因此选用铣削的加工思路进行分析研究。在仿形铣切第二阶段中，锯切的面积比较大，因此选择粗铣的方式进行分析。粗铣阶段每齿进给量fz=0.30 mm/z

由此，结合齿数z=50，可以求得进给速度，其计算方式如下

vf=fz·n·z=50 mm/s

(3)

2.2 锯切力的计算

1)可知，锯切功率的公式为

(4)

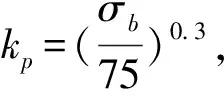
(5)

圆周铣削力为

(6)

侧吃刀量ae是指在平行于工作平面并垂直于锯切刃基点的进给运动方向上测量的吃刀量。如图2中AC所示。

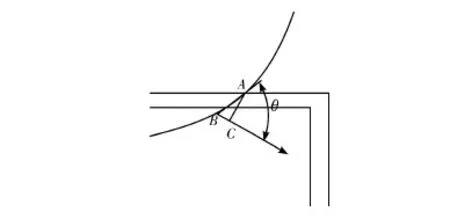
图2 锯切方向示意图

锯片在对钢管进行锯切，与钢管外侧的交点为A点，内侧的交点为B点，锯片中心运动方向在拐角处由水平运动变为垂直运动，在此过程的锯片中心运动如箭头所示，此时的侧吃刀量ae计算如下

ae=AC=IAB×sinθ

(7)

由此只需给出A、B两点间距离以及运动方向与AB的夹角θ即可。然后使用ADAMS软件进行仿真并得出相关结论。

3 基于ADAMS的仿真

前期已在三维建模软件Solidworks中完成建模，如图3所示。将模型导入到ADAMS中添加运动副等，完成在ADAMS中的建模，如图4所示。将运动过程中锯片中心的坐标以及锯片运动的速度与方向作为有关变量，进行分析与研究。

图3 仿形飞锯机锯切系统SolidWorks图

图4 仿形飞锯机锯切系统 ADAMS效果图

3.1 锯片中心位置的计算

在已经完成建模以及添加运动副的基础上，选用直接在锯片的中心位置指定运动的方式添加运动，即在笛卡尔坐标系下直接输入中心的位置的坐标与时间的关系式，使其坐标随着时间的变化而变化，从而完成运动仿真。如图5所示，选择加工时刀具距离钢管外侧100 mm处为锯片中心所在位置，由于钢管尺寸为300 mm×300 mm，两个刀片圆心的初始坐标为(0,250)和(0，-250)，锯片中心行走的轨迹在圆角处的半径分别设为R，R即为优化目标。由于两个锯片的运动轨迹完全相同，本文以其中一个为例进行研究。在图5中一个刀具的轨迹被A～F六个节点分为了五个阶段，其中第一、第三、第五阶段轨迹为直线，第二、四阶段轨迹为圆弧。

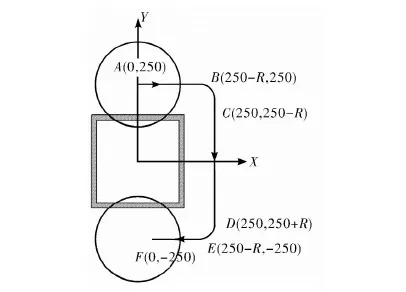
图5 切削轨迹图

由图5可知，锯片从起点A运行到节点B的距离为250-R；

从节点B到节点C的距离为四分之一圆，运行距离为0.25×2×π×R，从A到C总运行距离为250-R+0.25×2×π×R=250-R+0.5×π×R；

以此类推，运行到节点D的总运行距离为250-R+0.5×π×R+2×(250-R)=750-3R+0.5×π×R；

运行到节点E的总运行距离为750-3R+0.5×π×R+0.5×π×R=750-3R+π×R；

由式(3)可知进给速度Vf，由此可得各段运行时间。

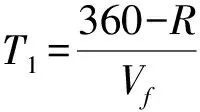
锯片运行到节点C的时间

锯片运行到节点D的时间

锯片运行到节点E的时间

在ADAMS软件中，将半径R设为参数化变量，即R=DV_1，建立测量函数，将四个节点时间输入，其表达式分别为

T1=(250-DV_1)/50

(8)

T2=(250-DV_1+0.5*PI*DV_1)/50

(9)

T3=(750-3*DV_1+0.5*PI*DV_1)/50

(10)

T4=(750-3*DV_1+PI*DV_1)/50

(11)

设钢管中心点为(0,0)，在第一阶段钢管切入圆弧之前，锯片中心位置的坐标为

X=vt=50×t，Y=250

考察切入圆弧以后的移动规律，由于锯切速度始终恒定，则圆弧阶段角速度为v/R=50/R，单位为弧度rad，可知在圆弧阶段t时刻走过的角度为(t-T1)×(v/R)，t时刻锯片中心位置相对T1时刻的横坐标增量为R×sin[(t-T1)×(v/R)]，纵坐标增量为R×cos[(t-T1)×(v/R)]，在这一阶段，锯片中心位置的坐标为

X=250-R+R×sin[(t-T1)×(v/R)]

Y=250-R×cos[(t-T1)×(v/R)]

以此类推，可以推倒出在运行过程中锯片中心的全部的位置坐标，如表3所示。

表3 锯片中心位置坐标汇总表

3.2 锯片与钢管内外壁交点的位置

将钢管的中心设定为坐标原点如图6所示。以锯片和钢管外侧交点为例进行分析，再将结论推广到锯片与钢管内侧的交点。当交点位于第一象限时，交点的坐标分为两种情况，分别为锯片和钢管交于Y=150(图6中实圆的情况)及交于X=150(图6中双点划线圆的情况)。两种情况A点坐标经数学推导后，标于图6上，且A点坐标无论XY值均不能大于150 mm。

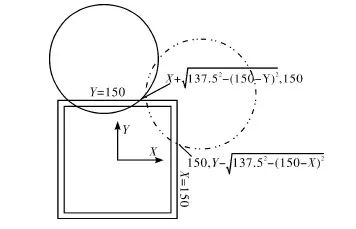
图6 笛卡尔坐标系下的示意图

在ADAMS中对锯片中心的坐标建立测量，分别命名为Px、Py，这两个变量将会伴随着仿真的进行自动变化。

3.3 侧吃刀量的计算

将锯片中心的移动方向定义为运动方向，在笛卡尔坐标系下，分析锯片运动方向与锯片切削刃之间夹角的表达式。

图7以锯片沿圆弧在直角坐标系第一象限中的情况为例进行分析，当运动方向如图7中箭头所示时，运动方向与切削刃AB之间的夹角θ由两部分组成，分别为切削刃AB与水平方向夹角α，运动方向与水平方向夹角β，则有

设运动速度在横纵坐标上的投影分别为vx，vy，可知

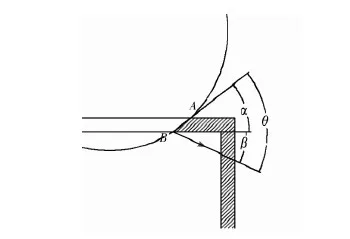
图7 锯片运动方向示意图

在ADAMS中建立测量，可求得运动在横纵坐标上的分速度。

3.4 载荷的综合表达式

根据侧吃刀量的公式ae=AB×sinα，定义吃刀量在ADAMS中的表达式。

选用在仿真软件中加转矩的方式加载，转矩

由此得到载荷在ADAMS中的综合表达式。

4 仿真与优化

为了使机构在加工过程中不会产生空行程，提高工作效率，将切削轨迹半径R的最小值设定为116 mm，由于设备结构限制，将半径的最大值设为170 mm。仿真完成后，使用ADAMS后处理模块进行分析，锯片中心位置坐标分别如图8、图9所示，与预期的运动状况相符，模型建立正确。

图8 锯片中心横坐标的变化规律

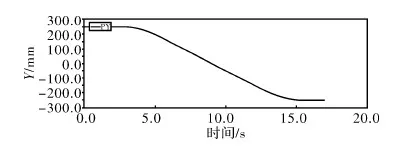
图9 锯片中心纵坐标的变化规律

对锯切运动的功率进行分析，当R=116时功率曲线如图10所示，

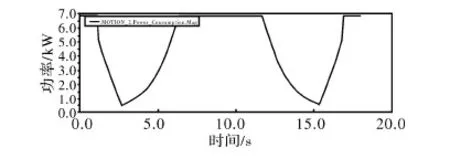
图10 R=116 mm时的功率变化规律

从图中可以看到，在锯切圆弧处存在锯切功率的减小，与预期相符合。功率的最大值6.76 kW，也与预期值相符。可以看到，功率的最小值为0.52 kW，非常小，功率的波动很大。

以R为变量 ，以输出功率最小值最大为优化目标进行优化设计R变化范围116～170 mm，进行优化设计，当R=160 mm时，得到最优解，如图11所示，功率的最小值为2.45 kW，功率的波动得到了缓解。

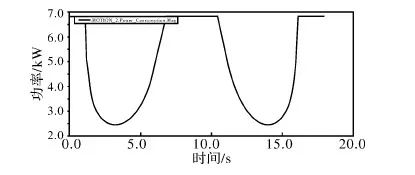
图11 R=160 mm时的功率变化规律

R/mmPmax/kWPmin/kWδ/%R=1166 870 5292 43R=1606 872 4559 97

5 结束语

以300 mm×300 mm钢管的锯切加工为例，给出了锯切功率的计算方法，并采用ADAMS软件进行仿真分析、优化设计，给出了锯片中心的最优运动轨迹，在此运动轨迹下，得到功率最优解，功率波动由92.43%降低到59.97%，提高了工作效率，降低了力矩波动系数，使得运行平稳，噪音低，冲击振动小。目前已将该研究应用到生产线上。

参考文献：

[1] 成大先.机械设计手册(五版)[M]. 北京：机械工业出版社，2010.

[2] 任星,张玉华,宋新环,等. 钢管仿形铣切飞锯机锯片的研究[J].重型机械,2016,(01):33-38.

[3] 邱宣怀.机械设计(五版)[M].北京:高等教育出版社，1997.

[4] 张策.机械原理与机械设计[M].北京:机械工业出版社，2004.

[5] 申永胜.机械原理教程[M].北京:清华大学出版社，1999.