基于EEMD样本熵与LS-SVM的行星齿轮箱故障诊断

任国春,赵永东

（装甲兵工程学院机械工程系,北京100072）

0 引言

1s，共40组试验数据。图 1为行星齿轮箱故障模拟试验台。

行星齿轮箱的运行工况变化频繁，承受着动态重载载荷，其中太阳轮、行星轮、齿圈等行星齿轮箱的关键部件经常发生诸如裂纹、磨损、点蚀、断齿等故障。因此，研究行星齿轮箱故障诊断具有重要意义[1]。

故障诊断的关键是故障特征参量的提取，集合经验模态分解（EEMD）适合于分析非线性、非平稳类信号，是一种后验的、自适应的分解方法。样本熵可以对信号的复杂程度进行度量，其优越性在于参数改变时样本熵结果的一致性较好[3]。LS-SVM算法是由Suykens提出的对SVM进行的改进，其用最小二乘线性系统作为损失函数，提升了运算速率，适用于小样本数据分析，并在故障识别中具有较高的识别精度与速度[4-5]。

本文利用EEMD方法将采集到的齿轮振动信号分解为若干IMF分量，提取不同层的IMF分量样本熵作为故障特征向量，输入到LSSVM分类器中，对行星齿轮箱齿轮正常、太阳轮裂纹、行星轮裂纹等状态进行识别，证明了该方法的有效性。

齿轮正常、太阳轮裂纹、行星轮裂纹故障对应的振动信号时域和频域波形图如图2所示，从图中无法识别出相应的故障特征。

1 基本原理

1.1 EEMD原理

为了解决EMD算法中存在的混叠现象，EEMD算法采用以下方式予以消除：将高斯白噪声叠加在原始信号中并进行多次EMD分解，最终计算结果取多次分解得到的IMF分量的均值。

EEMD方法将原信号分解为由高频到低频的若干个IMF分量和一个余量ri( t )，从而得到原信号在不同频率上的窄带分量。

1.2 样本熵原理

样本熵度量时间序列复杂性表现为为：时间序列越复杂，样本熵值越大，反之，样本熵值越小。根据文献[3]的研究结果及多次试验对比分析，当m=2，r = 0 .15×Std （Std为信号的标准差）时，信号的样本熵计算更为合理，可以有效的进行特征提取分析。

对3种状态的齿轮振动信号进行EEMD分解，获得若干IMF分量，其中添加的白噪声幅值系数k =3，总体平均次数N =100；分解结果的前6层IMF分量分别如图3所示。

2 齿轮故障诊断

2.1 算法流程

（1）利用EEMD将齿轮的振动信号分别分解为若干IMF分量；

（2）求解各IMF分量与原信号的互相关系数，对互相关系数大于0.1的IMF分量计算样本熵，作为输入到LS-SVM分类器中的特征向量；

（3）将上述特征向量组成的数据集分为训练样本和测试样本，将训练样本输入到LS-SVM中进行训练并建立模型；将测试样本输入到训练好的LS-SVM模型中进行分类，确定齿轮的故障类型。

2.2 应用实例

试验装置由可控电机，行星齿轮箱、涡流测功机及振动加速度传感器构成。试验分别设置齿轮正常、太阳轮裂纹、行星轮裂纹三种故障类型，电机转速为2400r/min，采样频率为5120Hz，采样时间为

计算EEMD分解后的IMF分量与原信号的互相关系数，求解与原信号互相关系数大于0.1的IMF分量的样本熵，并作为特征向量输入到LS-SVM分类器中进行故障识别。表 1为各IMF分量与原信号的互相关系数的均值。

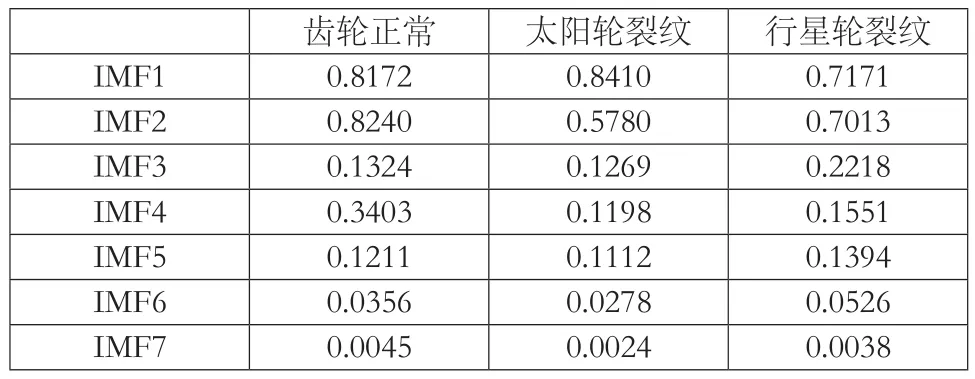
表1 各IMF分量与原信号的互相关系数

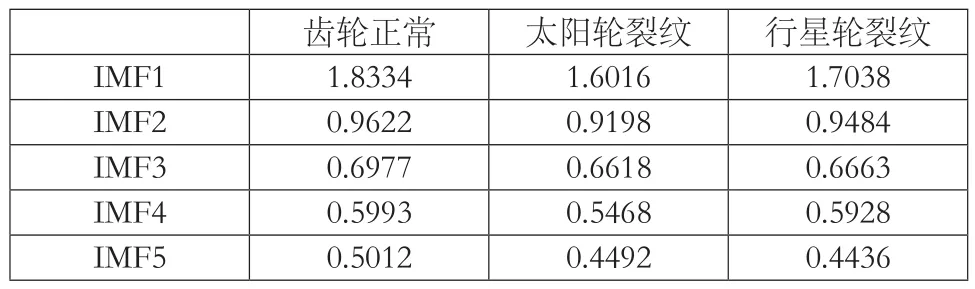
表2 3种齿轮状态的IMF分量的样本熵

由表1可知，与原信号互相关系数大于0.1的IMF分量为1～5层，表 2为3种齿轮状态的IMF1～5层分量的样本熵均值。

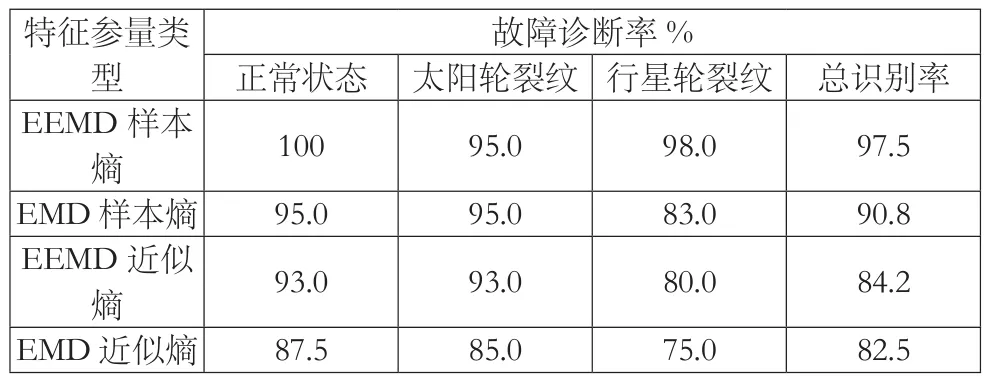
表3 不同熵的故障识别率

将提取的齿轮振动信号EEMD样本熵作为特征向量输入到LSSVM分类器中判断齿轮状态，试验中随机抽取共20组样本数据作为训练集，20组作为测试集。LS-SVM计算中使用径向基核函数，用交叉验证方法优化核函数参数及惩罚因子。作为对比，本文分别对每种状态每组齿轮振动信号进行EEMD与EMD分解，再分别计算各自IMF分量的样本熵与近似熵，实验结果如表3所示。

由表3可知，以EEMD分解后的样本熵、近似熵作为特征参量的故障识别率均高于EMD，EMD分解中存在模态混叠现象使信号分解不准确，导致样本数据无法准确识别。EEMD及EMD样本熵的故障识别率均高于相应的近似熵，证明了样本熵对振动信号的复杂性度量优于近似熵。因此，基于EEMD样本熵与LS-SVM的故障诊断有很好的故障识别准确率，能够区分出齿轮不同故障状态。

3 结论

本文采用EEMD样本熵与LS-SVM方法对行星变速箱齿轮进行故障诊断，实例结果表明：

（1）对实测齿轮振动信号分析表明，样本熵能够度量齿轮不同故障状态下的信号复杂性，可以作为判断齿轮故障的特征参数，并与近似熵进行对比，证明样本熵作为齿轮故障特征参量性能优于近似熵。

（2）经过互相关系数法筛选出的IMF分量包含了齿轮振动信号的关键状态信息，将计算所得的样本熵值作为特征参量输入LS-SVM分类器中，通过试验验证了该方法的有效性，识别出行星齿轮箱不同故障类型。

[1]冯占辉,胡茑庆,程哲.基于时频域状态指标的行星齿轮断齿故障检测[J].机械科学与技术,2010,29(06):701-704.

[2]郑近德,程军圣,杨宇.改进的EEMD算法及其应用研究[J].振动与冲击,2013,32(21):21-26+46.

[3]苏文胜,王奉涛,朱泓,郭正刚,张志新,张洪印.基于小波包样本熵的滚动轴承故障特征提取[J].振动.测试与诊断,2011,32(02):162-166+263.

[4]丁国君,王立德,申萍,杨鹏.基于EEMD能量熵和LS-SVM的传感器故障诊断[J].传感器与微系统,2013,32(07):22-25.

[5]陈仁祥,汤宝平,杨黎霞,周广武.自适应参数优化EEMD机械故障特征提取方法[J].振动.测试与诊断,2014,34(06):1065-1071+1169-1170.