波纹膜片的设计方法研究

聂绍忠

(重庆四联测控技术有限公司，重庆 401121)

0 引言

膜片是差压传感器的核心弹性元件，不仅起保护作用，而且其性能对差压传感器的特性影响较大。弹性元件在压力作用下的弹性滞后、弹性后效以及蠕变等非弹性效应会影响传感器的测量误差、长期零点漂移误差等特性。通过选择高弹性的材料、匹配的膜片参数以及型面参数，保证传感器的综合性能。本文选择量程为0～100 kPa、正负侧保护压力为300 kPa的差压传感器设计膜片。

1 波纹膜片材料的选择

用于传感器的弹性元件要求其工作特性必须恒定，因此应该选用具有高弹性极限的金属材料。材料的弹性极限越高，材料的弹性储能就越大，非弹性效应就越小。材料弹性储能公式如式(1)所示：

(1)

式中：σp为材料弹性极限；E为材料弹性模量。

目前，国内常用的高弹性合金材料有17-4PH(630)、铍青铜、Ni42CrTiAl(3J53)、3J58，它们具有弹性高、滞后蠕变小、耐腐蚀性能好等特性，它们的机械力学性能如表1[1]所示。

将17-4PH(630)材料的机械力学性能参数代入弹性储能公式，可得：

(2)

将铍青铜材料的机械力学性能参数代入弹性储能公式，可得：

(3)

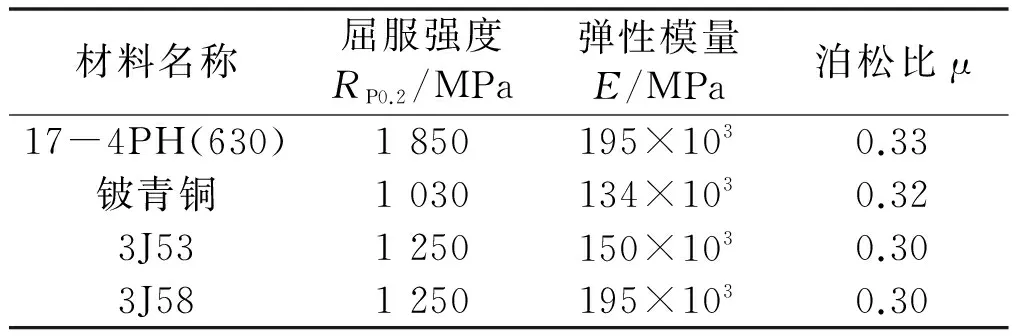
表1 机械力学性能

将 3J53材料的机械力学性能参数代入弹性储能公式，可得：

(4)

将 3J58材料的机械力学性能参数代入弹性储能公式，可得：

(5)

根据以上计算可得，17-4PH(630)具有更高的弹性储能性能、较小的滞后蠕变趋势，材料的延展性为7%，易于成型加工，且具有较高的抗腐蚀和氧化性。因此，本文选择17-4PH(630)作为膜片的材料。

2 膜片各参数的确定

膜片的尺寸参数很多，不能像计算力学问题那样，完全由力学方程直接得出。必须根据膜片的压力特性方程、仪器仪表结构以及工艺条件等因素，初步确定膜片的尺寸参数。

膜片的压力特性方程[2]如下：

(6)

式中：P为均布压力；R为膜片的工作半径；E为膜片材料的弹性模量；h为膜片厚度；KP为弯曲刚度系数；LP为拉伸刚度系数；AP为无量纲刚度系数；BP为无量纲拉伸非线项系数；WO为膜片中心的形变量。

(7)

(8)

(9)

式中：H为膜片的波纹高度。

由膜片的压力特性方程可知，影响膜片位移量变化的主要参数为膜片的工作半径、膜片的厚度、膜片的波纹高度、膜片的波纹半径以及材料的机械性能。

膜片参数除了对膜片特性影响较大外，对膜片的波纹形状也有较大的影响。通常，波纹形状主要有正弦形、梯形、锯齿形。波纹形状对膜片特性影响如图1所示。由图1可知，梯形、锯齿形的特征较正弦形好。然而这两种波形成型加工较为困难，对膜片材料的拉伸比较大，在直角边存在应力集中的情况。由于膜片在传感器中始终受交变力作用，为了保证传感器的经久耐用，经综合考虑选择正弦形波纹。

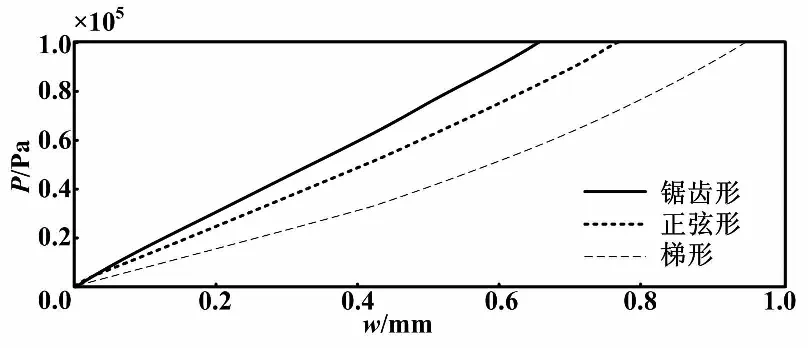
图1 波纹形状对膜片特性影响曲线

3 有限元模型建立

在进行分析之前，必须先建立有限元模型。在建立膜片模型时，需对膜片的受力状况作一定的简化和假设：①假设膜片材质均匀无杂质；②忽略膜片加工过程中的冷作硬化，但前提是必须保证研究对象的基本特征和受力状态不被改变。本模型可接受的模型为实体和曲面模型。实体模型采用3-D 实体元素建立网格，无需定义截面特性；曲面模型采用2-D 元素建立网格，必须定义截面厚度。根据初步设定的膜片参数以及实际安装尺寸等条件，采用CAD软件创建模型。

4 指定材料、元素和截面

在运行一个静力结构分析前，需定义指定的分析类型所响应需要的材料属性。本文选用17-4PH(630)作为本次设计的弹性材料，材料参数如表2所示。

表2 材料参数

每一个壳体[3]具有不同的材料参数。材料参数的指定可直接使用系统提供的材料数据库，或设置材料的特性参数，如弹性系数、密度、泊松比与剪弹性系数等。关于材料的单位，可视应用条件选择相应的单位。本文统一选择SI/Nm2(Pa)为运行计算单位。材料包含了等向性或非等向性材料。等向性材料每个方向的材料性质相同，而非等向性材料在各方向则有不同的材料参数值。例如，在等向性材料中，杨氏系数只有EX一个，其他方向的刚性相同。而非等向性材料在X方向杨氏系数为EX，在Y方向杨氏系数为EY，而在Z方向杨氏系数为EZ，其EX、EY、EZ各不相同。经测试表明，17-4PH(630)为等向性材料，因此杨氏系数只有EX。材料17-4PH(630)的弹性模量E为1.95 GPa、泊松比μ为0.33、屈服强度RP0.2为1 850 MPa 。

5 网格生成

网格划分是一个重要步骤。网格用于描述几何模型的物理模型。它是进行有限元分析之前的必需步骤。程序将模型划分为许多具有简单形状的小块，这些小块通过公共点连接，这个过程就称为网格划分。有限元分析程序将集合模型视为一个网状物，这个网是由离散的互相连接在一起的小块元构成的。固体网格适用于大体积和复杂几何形状的模型。壳网格适用于薄的零件，如钣金零件、膜片零件等。分析精度很大程度依赖于网格划分的质量。本文所计算的膜片厚度预计不会超过0.5 mm，因此视为薄壳零件，进行网格划分时采用了壳网格。膜片网格划分效果如图2所示。

图2 膜片网格划分效果图

6 载荷与约束

边界条件施加与工程实际是否吻合直接影响分析结果的正确性、合理性。

要完成加载，必须经过以下过程。

①选择分析类型并针对分析类型设置分析选项。

②施加各种载荷，这里的载荷是广义的载荷，包括自由度、载荷和边界条件。

③设置载荷及其他选项。

根据膜片的实际工作情况，对膜片进行边界条件分析，对其模型添加约束和载荷，载荷和位移约束加在单元和节点。膜片采用四周焊接的方式固定在传感器内腔，膜片的固定区域在直径D与d之间。膜片在直径d区域上承受均布压力P,膜片受力分析如图3所示。根据膜片实际的固定和受力情况，在三维模型上定义约束和载荷，膜片的边界约束和均布载荷如图4所示。

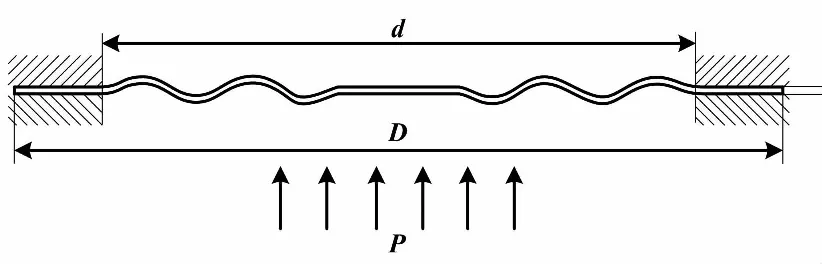
图3 膜片受力分析图

图4 边界约束和均布载荷图

7 运行分析

当膜片的材料设定、网格划分、负荷和约束完成后，就可以进行运行分析了。分析过程中，分析软件系统将显示分析元素、节点数以及自由度。

7.1 结果显示

运行分析后，系统自动生成每种类型的结果报告。分析软件为静态分析产生标准的输出项。通过选择点击相应的输出项，观察分析的结果。图5为膜片静态位移和应力分布图，图6为膜片静态位移变化和应力变化曲线图。

由图5和图6可知，膜片在均布压力作用下最大位移量出现在膜片的中心区域，其值达到0.316 4 mm，这与膜片的实际变形情况相吻合。膜片在均布压力作用下，最大应力出现在膜片起波的位置，即挠度变化比较大的位置，其等效应力为最大值474.3 MPa。其他部位应力较最大应力偏小，这也与实际情况相吻合。

图5 静态位移和应力分布图

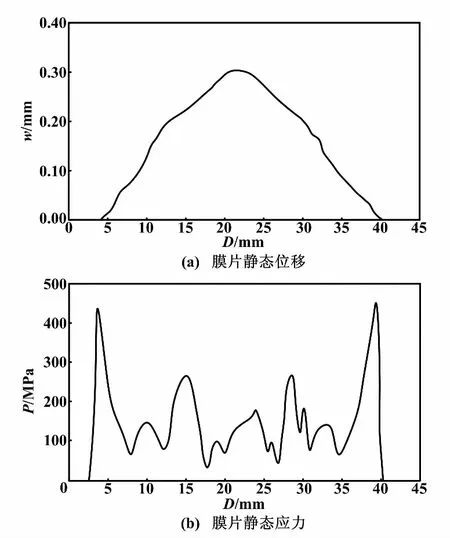
图6 静态位移和应力变化曲线图

有限元分析不仅可以直观反映膜片在均布压力作用下的最大位移量发生区域，而且也可以清楚反映膜片在受力作用下产生最大应力的区域。

根据传感器的特性以及弹性材料的最大变形量要求，膜片在极限保护压力作用下的最大形变位移量必须控制在(0.3±0.02)mm以内。为了减小弹性滞后、弹性后效以及蠕变，最大的应力不得大于材料极限应力的30%，即555 MPa。由于传感器的结构特性，要求膜片的工作半径必须控制在20 mm以内。如前面所述影响膜片位移量变化以及应力应变的主要参数为膜片的工作半径、膜片的厚度、膜片的波纹高度、材料特性。由于膜片的工作半径已确定，那么只有通过调整膜片的厚度、波纹高度以及波纹半径，满足传感器的特性以及弹性材料的最大变形量要求。表3所示为膜片调整参数。

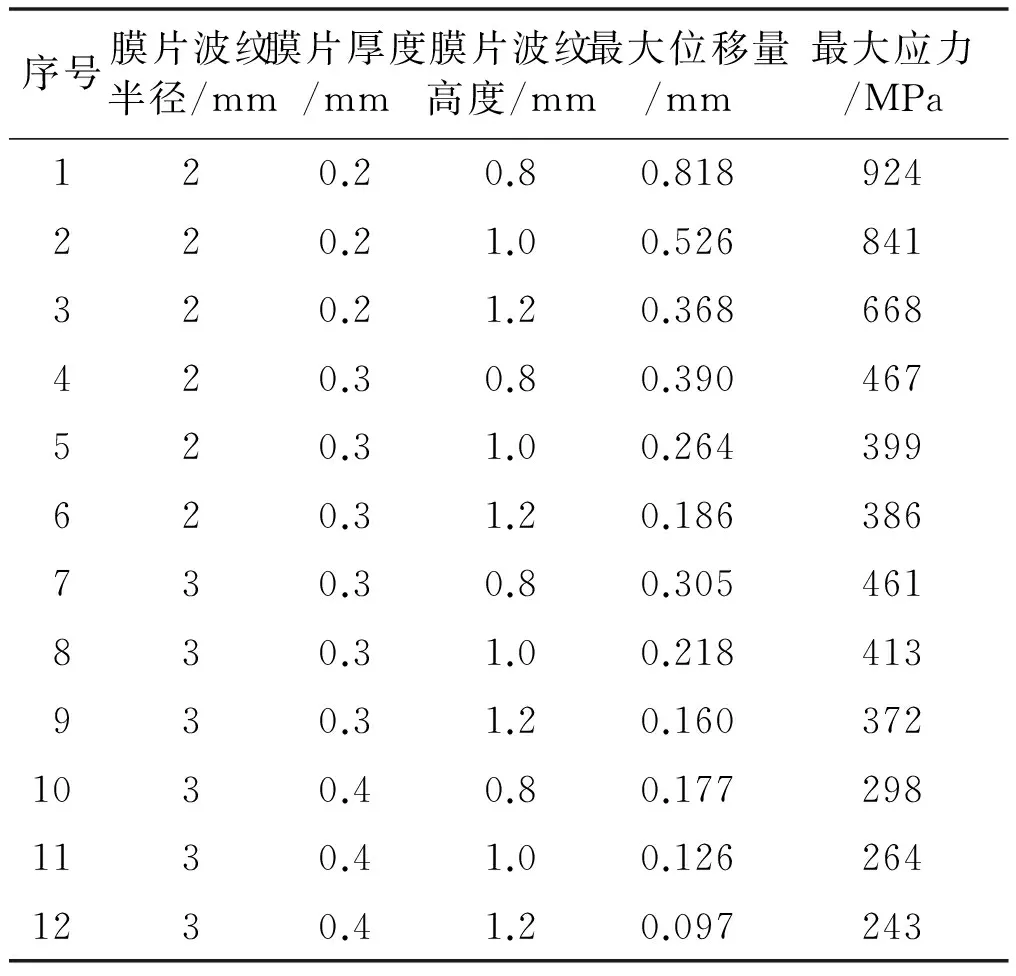
表3 膜片调整参数

从表3可得，第7组数据更接近传感器特性以及弹性材料的最大变形量要求。根据该组数据，结合膜片的安装直径以及膜片的工作半径，加工膜片实物。

7.2 验证

为了验证本文方法的准确性，进行了实物膜片测试和传感器测试。实物膜片测试包括位移量、弹性后效以及弹性蠕变测试。传感器测试，即把实物膜片焊接在传感器内，对传感器的长期零点漂移进行测试。

7.2.1 实物膜片测试

按装夹方式对膜片固定，然后在膜片一侧加不同压力的气压，另一侧与高精度的测量仪器探头接触，进行位移测试。随着压力的变化，得出一系列位移量，然后把这一系列的位移量与有限元所分析所得的理论位移量对比，如表4所示。由表4可见，实测的位移量与分析所得的理论位移量的误差小于10%。

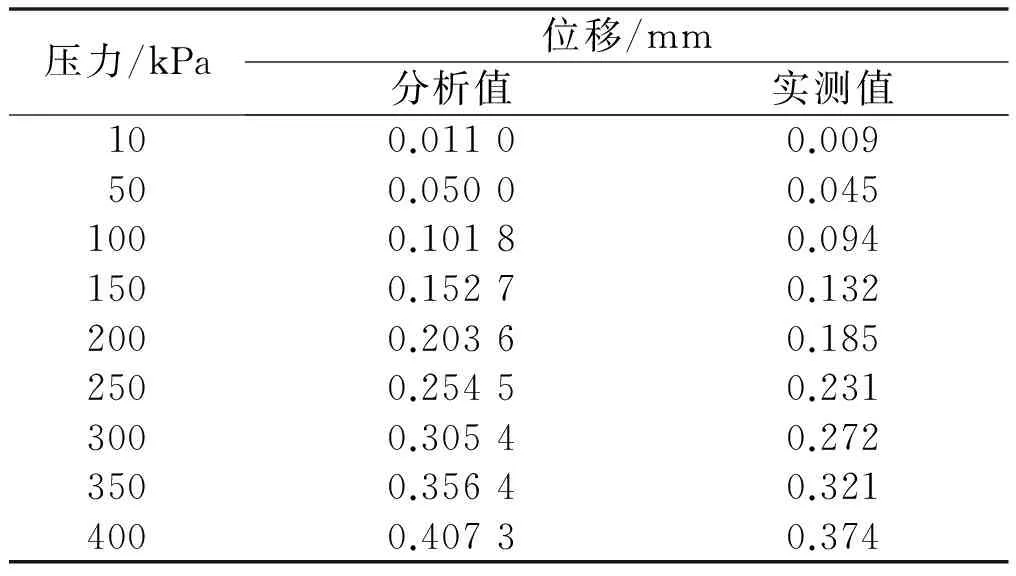
表4 不同压力的有限元位移分析值和实测值

弹性后效以及弹性蠕变的测试方法与膜片位移量的测试方法类似。只是压力为一定值，测量仪器检测膜片在相同压力下，随着时间的推移，膜片的位移量是否增大。弹性后效以及蠕变的测试数据如表5所示。膜片在300 kPa的压力作用下，产生的弹性后效以及蠕变变化量为0.002 mm。该变化量非常小，在实际中完全可以忽略不计。

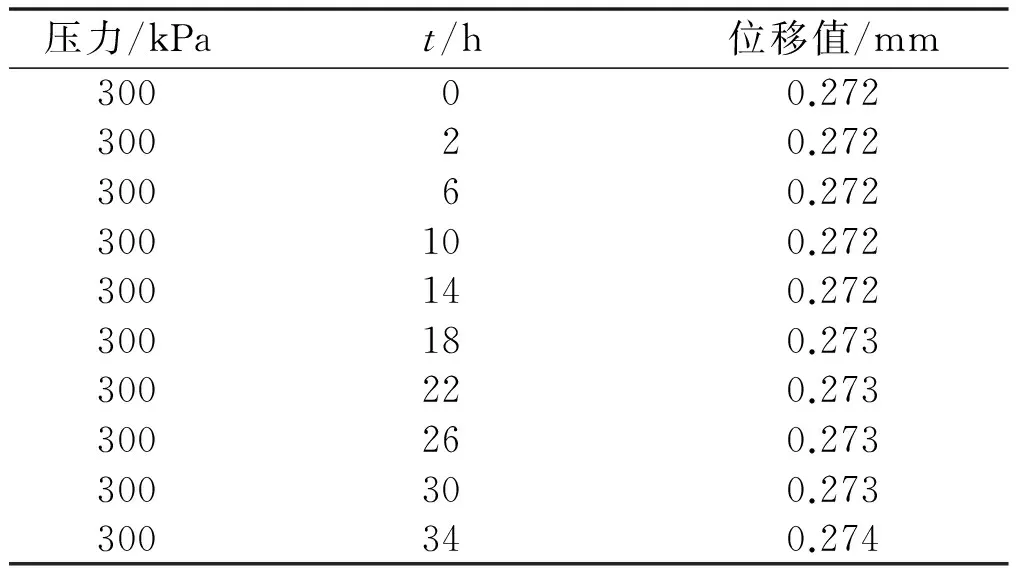
表5 同压力下膜片位移量变化表

7.2.2 长期零点漂移测试

为了进一步验证膜片，对装配有膜片的传感器[4-10]

进行长期零点漂移测试，并通过测试软件记录测试数据，经过连续168 h的测试，零点电压输出最大误差0.001 V,远低于行业标准0.008 V。

通过以上验证可以得出，采用本文方法设计的膜片位移量基本接近理论计算值，弹性后效以及蠕变小、传感器的长期零点漂移小，完全能够满足传感器的使用要求。

8 结束语

本文通过采用膜片的压力特征方程与有限元分析软件相结合的方法，对膜片进行了详细设计，并对膜片进行了一系列的测试和验证。结果表明，利用该方法设计的膜片精度高、可靠实用，完全能够满足传感器的要求，对于类似膜片的设计具有一定的参考意义。

[1] 李科杰.新编传感器技术手册[M].北京：国防工业出版社,2001：169-175.

[2] 樊大钧.金属膜片的设计[M] .北京：北京机械工业出版社，1987：101-120.

[3] 卢海星.SolidWorks 2014有限元、虚拟样机与流场分析从入门到精通[M].3版.北京：国防工业出版社，2014：20-30.

[4] 吴立志 王兴国.基于ABAQUS的隔膜压缩机膜片有限元分析[J].北京石油化工学院学报，2008,16(4)：13-16.

[5] 郝正宏,王徐坚,李俊毅,等.高稳定性单晶硅压力(差压)变送器的实现[J].自动化仪表,2015,36(4):91-95.

[6] 王骏,叶瑞源.基于HART6的智能压力变送器设计[J].自动化仪表,2008,29(7):3-6.

[7] 方原柏.压力差压变送器的性能误差研究[J].自动化仪表,2017,38(1):69-72.

[8] 王峰,谭晓兰,张敏亮.压阻式微压力传感器结构参数设计[J].自动化仪表,2013,34(3):83-86.

[9] 陈东宇,施一明,金建祥.基于HART协议的智能扩散硅压力变送器[J].自动化仪表,2001,22(6):17-19.

[10]王徐坚.金属电容式传感器的静压影响误差[J].自动化仪表,2008,29(12):18-20.